§3. Интегрирование тригонометрических функций

1. Интегралы вида в общем случае вычисляются с помощью универсальной тригонометрической подстановки . При этом

, ,

и подынтегральная функция станет рациональной функцией от .

Если – нечетная функция относительното интеграл вычисляется с помощью подстановки

Если – нечётная функция относительно,то используется подстановка

Если – четная функция относительното интеграл вычисляется с помощью подстановки;

2. Интегралы вида приводятся к табличным с помощью формул:

3. Для интегралов вида .

3.1. Если хотя бы одно из чисел т, п – нечетное (например, m = 2k + 1), то

.

3.2. Если т и п – четные, положительные, то степени понижаются сведением к двойному углу по формулам

3.3. Если т, п – четные и хотя бы одно из них отрицательно (или если т и п – отрицательные числа одинаковой четности), то используем соотношения

Типовые примеры

Вычислить интегралы.

1. .

►Выполняя подстановку и используя формулы (12), интеграл запишем в виде:

◄

2. .

►◄

3..

►◄

4..

►Используя формулу (3), получим

.◄

5..

►◄

6..

►

◄

7. .

►◄

8. .

►◄

§4. Интегрирование иррациональных выражений

1. Интегралы вида , где– целые числа, сводятся к интегралу от рациональных функций заменой переменной, где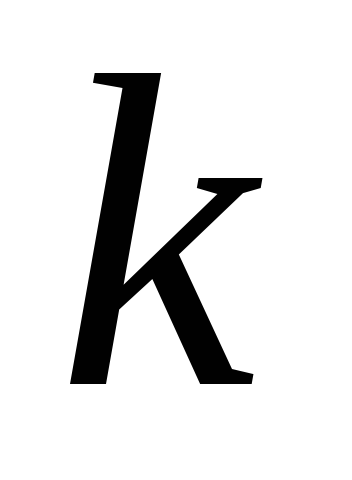– наименьшее общее кратное чисел(НОК).

Интегралы более общего вида

и

находятся (приводятся к рациональному виду) с помощью аналогичных подстановок: и.

2. Интегрирование дифференциального бинома

Дифференциальным биномом называется выражение вида , где– рациональные числа,– действительные числа. Как доказал П.Л. Чебышев, интегралвыражается через элементарные функции только в трех случаях:

1) – целое число. Тогда данный интеграл сводится к интегралу от рациональной функции с помощью замены, где– общий знаменатель дробейи;

2) – целое число. В этом случае интеграл рационализируется с помощью замены, где– знаменатель дроби;

3) – целое число. Чтобы рационализировать интеграл, необходимо сделать замену, где– знаменатель дроби.

3. Интегрирование функций вида и

Интегралы от этих функций сводят к интегралу от функции вида , который, как мы знаем, всегда можно привести к интегралу от рациональной функции. Делается это с помощью одной из трех подстановок, называемых тригонометрическими:

1) (или) для;

2) (или) для;

3) (или) для.

После их применения под знаком корня оказывается квадрат некоторой тригонометрической функции, что и позволяет избавиться от иррациональности.

3. Интегрирование функций вида

Интеграл от такой функции можно найти несколькими способами. Проще всего привести его к виду, рассмотренному нами в предыдущем пункте. Для этого достаточно выделить полный квадрат под знаком радикала:

,

а затем сделать замену .

Интегралы вида , где– вещественные числа, в общем случае вычисляются одной из подстановок Эйлера:

, ; (9)

, ; (10)

или , (11)

где и– различные вещественные корни трехчлена.

Типовые примеры

Вычислить интегралы.

1..

►Т.к. НОК (2;3)=6, то делаем подстановку: и

Переходя к переменной , получим:

◄

2. .

►Сделаем замену переменной: x + 3 = t⁴. Тогда dx = 4 t³dt. Подставим полученные результаты в подынтегральное выражение:

◄

3..

►Это интеграл от дифференциального бинома:

,

где ,,. Так как числоявляется целым, то интеграл выражается через элементарные функции. Чтобы рационализировать интеграл, необходимо сделать замену. Откуда находим,

и

.

Возвращаясь к старой переменной , окончательно получаем

.◄

4. .

►Это интеграл от дифференциального бинома:

,

где ,,. Так как– целое число, то интеграл выражается через элементарные функции. Чтобы рационализировать интеграл, необходимо сделать замену. Откуда находим,и

.

Из теперь находим, что. Подставляя это выражение в результат интегрирования, окончательно получаем

.◄

5. .

►Выделив полный квадрат в квадратном трехчлене, получим:

, где u = x + 1. Теперь сделаем замену переменной: Подынтегральное выражение при этом примет вид

◄

Иногда от квадратичных иррациональностей можно избавиться с помощью замен другого типа.

6. .

►Сделаем так называемую обратную подстановку: .

Тогда

◄

7. .

►Выделим полный квадрат под знаком радикала:

и сделаем замену ,. Тогда

.

Полученный интеграл можно найти двумя способами:

1) это интеграл от дифференциального бинома, для которого число – целое;

2) к этому интегралу можно применить тригонометрическую подстановку .

Воспользуемся вторым способом. Тогда

и .

Следовательно,

.

Из теперь находим

,

и, подставляя в результат интегрирования, окончательно получаем

.

Замечания:

1) если использовать формулу , то окончательный ответ можно записать в виде

;

2) интеграл , к которому нас привела первая замена, носит промежуточный характер. Решение было бы более коротким, если бы мы сразу перешли от исходного интеграла к интегралу. Этого можно добиться, если «объединить» замены, т.е. после выделения полного квадрата под знаком радикала сделать замену.◄

Типовой пример

Вычислить интеграл

.

►Используем 1-ю подстановку Эйлера (9): . Возведем в квадрат обе части равенства. После сокращенияполучим:

; выразим теперь радикал через переменную :. Подставляя выраженные черезвеличины в, получим:. Делая подстановку;, получим:

◄