
- •Глава I. Неопределеннный интеграл
- •§1. Определение. Общие приемы и методы интегрирования
- •2. Свойства неопределенного интеграла
- •3. Таблица основных интегралов
- •4. Методы интегрирования
- •4.1. Непосредственное интегрирование
- •4.3. Интегрирование по частям Пусть две дифференцируемые функции изависят от. Тогда
- •§2. Интегрирование рациональных функций.
- •Интегрирование произвольных рациональных дробей Пусть дан интеграл вида
- •§3. Интегрирование тригонометрических функций
- •§4. Интегрирование иррациональных выражений
- •3. Интегрирование функций вида и
- •Глава II. Определенный интеграл
- •§1. Определение. Формула Ньютона–Лейбница
- •2. Условия существования определенного интеграла
- •3. Свойства определенного интеграла
- •§2. Методы вычисления определенных интегралов
- •1.2. Область задана в полярных координатах
- •2. Вычисление длин кривых
- •2.1. Определение спрямляемой кривой и длины кривой
- •2.2. Длина кривой в декартовых координатах
- •2.4. Кривая задана в полярных координатах
- •3. Объёмы тел вращения
- •3.2. Объём тела, получающегося при вращении кривой вокруг координатной оси
- •4. Площадь поверхности вращения
- •§4. Определенный интеграл в экономике
- •1. Экономический смысл определенного интеграла
- •2. Восстановление функций экономического анализа по их предельным характеристикам
- •3. Определенный интеграл в финансовом анализе
- •Глава III. Несобственные интегралы
- •§1. Интегралы с бесконечными пределами (несобственные интегралы первого рода)
- •2. Признак сравнения
- •3. Признак сравнения в предельной форме
- •§2. Несобственные интегралы от неограниченных функций (несобственные интегралы второго рода).
- •2. Признаки сравнения
- •3. Признак сравнения в предельной форме
- •Главное значение
- •Глава I V. Кратные интегралы
- •§1. Двойной и тройной интегралы, их свойства. Геометрический смысл двойного интеграла
- •2. Свойства двойных интегралов
- •3. Тройной интеграл
- •4. Геометрический смысл двойного интеграла
- •5. Вычисление двойного интеграла в декартовых координатах путем сведения его к повторному
- •Вопросы промежуточного контроля
3. Признак сравнения в предельной форме
Пусть
неотрицательные функции
![]() и
и![]() интегрируемы по любому отрезку
интегрируемы по любому отрезку![]() и пусть существует конечный
и пусть существует конечный![]() .
Тогда несобственные интегралы
.
Тогда несобственные интегралы![]() и
и![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Сравнение
интеграла
![]() со "стандартным" интегралом
со "стандартным" интегралом![]() в предельной форме даёт правило: если
при
в предельной форме даёт правило: если
при![]() неотрицательная функция
неотрицательная функция![]() – бесконечно большая порядка роста
ниже первого по сравнению с
– бесконечно большая порядка роста
ниже первого по сравнению с![]() ,
то
,
то![]() сходится; еслиf(x)
имеет порядок роста единица или выше,
то интеграл расходится.
сходится; еслиf(x)
имеет порядок роста единица или выше,
то интеграл расходится.
Типовые примеры
1.
 .
.
►Так
как при
![]()
 ,
и интеграл от большей функции сходится,
то данный интеграл сходится; ◄
,
и интеграл от большей функции сходится,
то данный интеграл сходится; ◄
2.
![]() .
.
►При
![]()
![]()
![]() ,
,![]() ,
интеграл расходится; ◄
,
интеграл расходится; ◄
3.
 .
.
►При
![]()
![]()
![]() ,
,![]() ,
интеграл расходится; ◄
,
интеграл расходится; ◄
4.
![]() .
.
►При
![]()
![]()
![]() ,
интеграл расходится.◄
,
интеграл расходится.◄
Несобственный интеграл от неограниченной функций
 называетсяабсолютно
сходящимся, если
сходится интеграл
называетсяабсолютно
сходящимся, если
сходится интеграл
 ,
иусловно
сходящимся,
если интеграл
,
иусловно
сходящимся,
если интеграл
 сходится, а интеграл
сходится, а интеграл расходится
(если сходится
расходится
(если сходится ,
то
,
то тоже обязательно сходится).
тоже обязательно сходится).
Типовой пример
Исследовать
на сходимость интеграл:

►Так
как
 ,
то исходный интеграл сходится абсолютно.
◄
,
то исходный интеграл сходится абсолютно.
◄
Главное значение
Пусть
![]() имеет особенность в точке
имеет особенность в точке![]() .
Тогда несобственный интеграл определяется
равенством
.
Тогда несобственный интеграл определяется
равенством![]() =
=![]() +
+![]() =
=![]()
Если
хотя бы один из интегралов, стоящих в
правой части, расходится, то интеграл
![]() тоже
расходится.
тоже
расходится.
Но
тогда можно рассмотреть предел
![]() .
Если этот предел существует, то его
называют главным значением интеграла
.
Если этот предел существует, то его
называют главным значением интеграла![]() и обозначают
и обозначают![]() .
.
Типовой пример
Вычислить
интеграл
![]() .
.
►Интеграл
является несобственным, т.к. при
![]() подынтегральная функция не существует.
подынтегральная функция не существует.

т.е. интеграл существует в смысле главного значения. ◄
Глава I V. Кратные интегралы
§1. Двойной и тройной интегралы, их свойства. Геометрический смысл двойного интеграла
 Рассмотрим
в плоскости Оху
замкнутую область D,
ограниченную линией L.
Разобьем эту область какими-нибудь
линиями на п
частей
Рассмотрим
в плоскости Оху
замкнутую область D,
ограниченную линией L.
Разобьем эту область какими-нибудь
линиями на п
частей
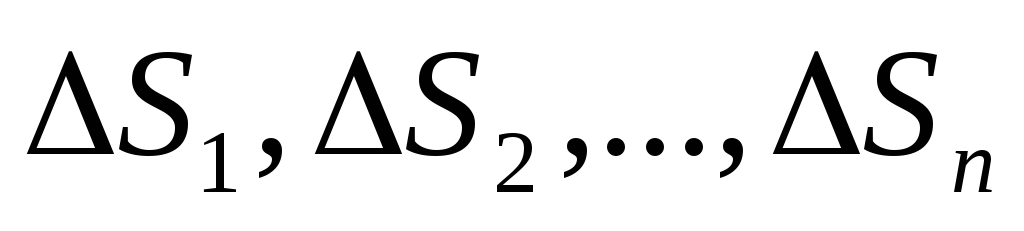 (причем
теми же символами
(причем
теми же символами будем обозначать и площади соответствующих
частей), а соответствующие наибольшие
расстояния между точками в каждой из
этих частей обозначимd1,
d2,
..., dn.
Величину di
будем называть максимальным
диаметром
подобласти
будем обозначать и площади соответствующих
частей), а соответствующие наибольшие
расстояния между точками в каждой из
этих частей обозначимd1,
d2,
..., dn.
Величину di
будем называть максимальным
диаметром
подобласти
 .
Выберем в каждой части
.
Выберем в каждой части точкуРi
(рис.1).
точкуРi
(рис.1).

Рис.1.
Пусть в области D задана функция z = f(x, y). Обозначим через f(P1), f(P2),…, f(Pn) значения этой функции в выбранных точках и составим сумму произведений вида f(Pi)ΔSi :
![]() .
(1)
.
(1)
Сумма
вида
![]() называется интегральной
суммой для
функции f(x,
y)
в области
D.
называется интегральной
суммой для
функции f(x,
y)
в области
D.
Замечание
С
геометрической точки зрения (при
![]() )
интегральная сумма (1) представляет
собой сумму объемов цилиндров с
основаниями ΔSi
и высотами
f(Pi).
)
интегральная сумма (1) представляет
собой сумму объемов цилиндров с
основаниями ΔSi
и высотами
f(Pi).
Если
существует один и тот же предел
интегральных сумм (1) при
![]() и
и![]() ,
не зависящий ни от способа разбиения
областиD
на части, ни от выбора точек Pi
в них, то он называется двойным
интегралом от функции f(x,
y)
по области
D
и обозначается
,
не зависящий ни от способа разбиения
областиD
на части, ни от выбора точек Pi
в них, то он называется двойным
интегралом от функции f(x,
y)
по области
D
и обозначается
![]() .
(2)
.
(2)
В этом случае функция f (x,y) называется интегрируемой в области D, область D – областью интегрирования, х и у – переменными интегрирования, dxdy = dS – элементом площади.
Замечание
Для выяснения вопроса об условиях интегрируемости функции двух переменных можно по аналогии со случаем определенного интеграла ввести понятие верхней и нижней интегральных сумм, выбирая в каждой части области D точки, значение функции в которых является наибольшим и наименьшим для данной части. Тогда можно доказать, что необходимым и достаточным условием интегрируемости функции f(x, y) является, во-первых, ее ограниченность на D, а во-вторых, условие
![]() (3)
(3)
где τ – некоторое разбиение, а Sτ и sτ – соответственно верхняя и нижняя интегральные суммы. Доказательство этого утверждения проводится так же, как для случая определенного интеграла.
Замечание
Аналогично одномерному случаю можно доказать еще одно утверждение: если функция f(x, y) непрерывна в замкнутой области D, то она интегрируема по этой области.
