5. Вычисление определителей -го порядка.

Пусть дана матрица -го порядка.Минором любого элемента называют определитель порядка, соответствующий той матрице, которая получается из матрицыв результате вычеркивания-й строки и-го столбца (т.е. той строки и того столбца, на пересечении которых стоит элемент). Минор элементабудем обозначать символом.

Алгебраическим дополнением элементаматрицыназывают минорэтого элемента, умноженный на, т.е.

.

ТЕОРЕМА. Определитель матрицы -го порядка равен сумме произведений всех элементов какой-нибудь одной фиксированной строки на их алгебраические дополнения, т.е. для любогоимеет место равенство

,

называемое разложением определителя по элементам-й строки.

Аналогично для имеет место разложение определителяпо элементам-го столбца:

.

Методы вычисления определителей:

1. Разложение по строке или столбцу.

2. Метод обращения в нуль всех, кроме одного, элементов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), все элементы выбранной строки (столбца) кроме одного обращаются в нуль, принадлежащего вычитаемому столбцу (строке).

3. Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, используется для последовательного преобразования определителя к треугольному виду. Величина такого определителя равна произведению элементов главной диагонали.

Типовые примеры

Вычислить определитель.

1. .

►Имеем , или, например,,

и т.д.◄

2. ►=0+(-45-91)+0= -136. ◄

3. .

►Вычислим данный определитель 4-го порядка с помощью разложения по 2-му столбцу. Для этого найдем и:

Следовательно,

◄

4. Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:

►Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец. Итак, имеем

П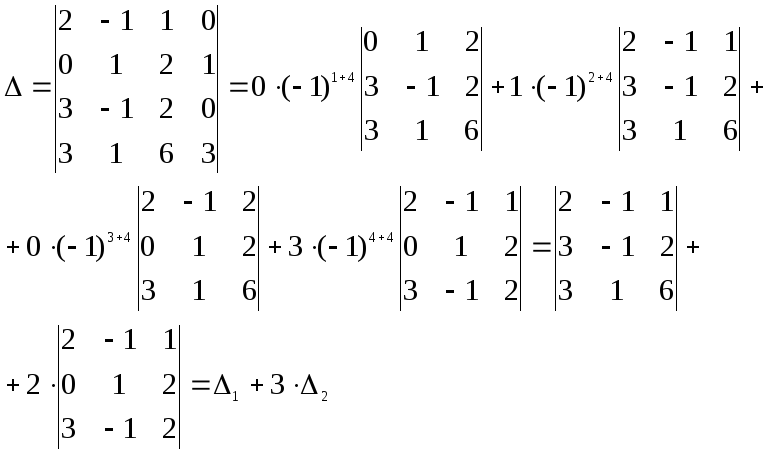олученные в итоге два определителя третьего порядка вычислим тем же методом. В определителенулевых элементов нет, поэтому можно выбрать для разложения любой из столбцов, например, первый. Вединственный нулевой элемент находится на пересечении первого столбца со второй строкой. Для разнообразия будем разлагатьпо второй строке:

.

.

Таким образом окончательно получим

.◄

5. Используя метод обращения в нуль всех, кроме одного, элементов строки или столбца вычислить определитель матрицы

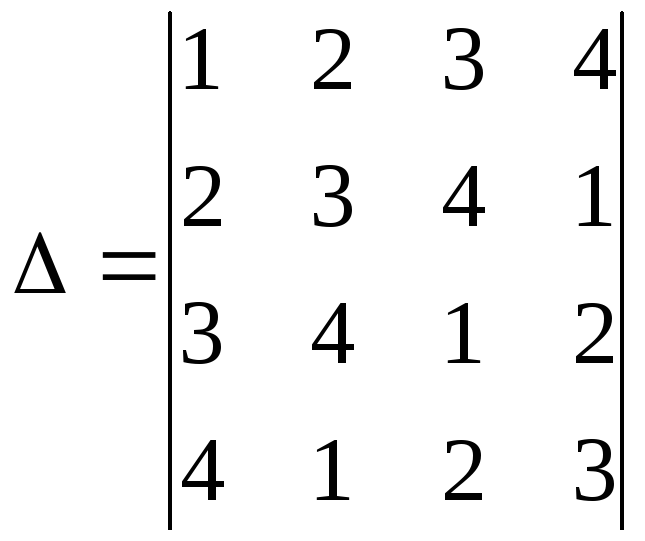
►Будем обращать в нуль все, кроме первого, элементы первой строки. С этой целью вычтем из второго, третьего и четвёртого столбцов первый столбец, умноженный соответственно на 2, 3 и 4. Получим

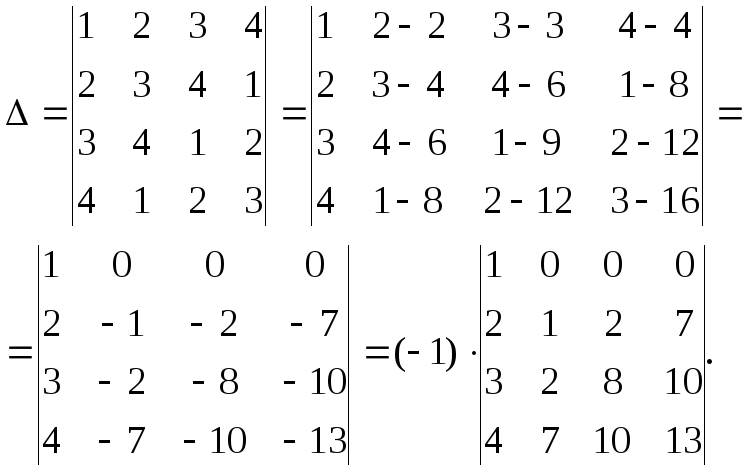
Представленный в таком виде определитель разложим по первой строке:

Определитель третьего порядка, к которому свёлся исходный определитель, будем вычислять тем же способом. Вычтем из второго и третьего столбцов первый столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)

◄

6. Используя метод приведения к треугольному виду вычислить определитель

►Воспользуемся видом определителя , который получился послепроцедуры обращения в нуль всех элементов (кроме первого) первой строки:

.

Далее с помощью второго столбца обратим в нуль элементы второй строки, кроме первых двух, для чего вычтем из третьего и четвёртого столбцов второй столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)

Наконец, вычтем третий столбец из четвёртого, в результате чего определитель сведётся к треугольному виду, величина которого равна произведению элементов главной диагонали:

.◄
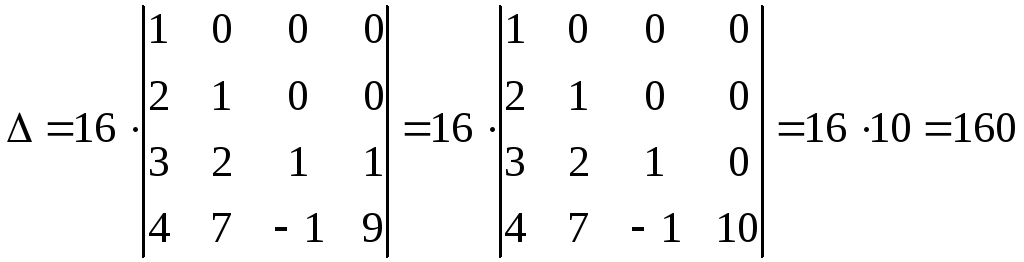