2. Базис и размерность линейного пространства

Фундаментальным вопросом теории линейных пространств является вопрос о том, можно ли, а если можно, то как, произвольный вектор пространства представить в виде линейной комбинации фиксированного набора векторов из этого пространства. Далее мы получим ответ на этот вопрос.

Система линейно независимых векторов векторного пространстваназываетсябазисом этого пространства, если любой вектор из может быть представлен в виде линейной комбинации векторов этой системы, т.е. для каждого векторасуществуют вещественные числатакие, что имеет место равенство

.

Это равенство называется разложением вектора по базису , а числаназываютсякоординатами вектора относительно базиса (или в базисе) .

Утверждение

Базисом линейного пространства решений одно­родной системы является ее фундаментальная система реше­ний.

ТЕОРЕМА (о единственности разложения по базису). Каждый вектор пространстваможет быть разложен по базису единственным образом, т.е. координаты каждого вектора в базисе определяются однозначно.

Главное значение базиса заключается в том, что операции сложения векторов и умножения их на числа при задании базиса превращаются в соответствующие операции над числами – координатами этих векторов. А именно, справедлива следующая

ТЕОРЕМА. При сложении двух любых векторов линейного пространства их координаты (относительно любого базиса пространства) складываются; при умножении произвольного вектора на любое число все координаты этого вектора умножаются на.

Типовой пример

Исследуем вопрос о базисе пространства , введенного ранее при рассмотрении Типовой примеров векторных пространств. Покажем, чтоэлементовуказанного пространства образуют базис.

►Во-первых, эти векторы линейно независимы. Проверка линейной независимости набора состоит в определении значений, при которых возможно равенство

.

Но в силу только что доказанной теоремы

,

а последний вектор является нулевым лишь при условии . Во-вторых, всякий векторзаведомо представим в виде линейной комбинации векторов:и, значит, наборобразует базис. ◄

Векторное пространство называется -мерным, если в нем существуютлинейно независимых векторов, а любыевекторов уже являются линейно зависимыми. При этом числоназываетсяразмерностьюпространства.

Размерность векторного пространства, состоящего из одного нулевого вектора, принимается равной нулю.

Размерность пространства обычно обозначают символом.

Векторное пространство называетсябесконечномерным, если в нем существует любое число линейно независимых векторов. В этом случае пишут.

Выясним связь между понятиями базиса и размерности пространства.

ТЕОРЕМА.Если – векторное пространство размерности, то любыелинейно независимых векторов этого пространства образуют его базис.

ТЕОРЕМА.Если векторное пространство имеет базис, состоящий извекторов, то.

Утверждение

Rⁿ=n.

Типовые примеры

1. Образуют ли базис в пространстве R³ векторы ?

►По определению базис составляют линейно независимые векторы. Линейная зависимость (или независимость) определяется исходя из анализа равенства нулю линейной комбинации этих векторов:

.

Последнее векторное уравнение после записи его по компонентам представляет собой систему трёх однородных уравнений относительно . Согласно схеме исследования линейной зависимости векторов вычислим определитель матрицы, составленной из координат векторов

Определитель системы равен нулю, следовательно, она имеет нетривиальное решение и это означает, что исходная группа векторов линейно зависима и не образует базис в R³. ◄

2.Найти размерность и один из базисов линейного пространства решений однородной системы:

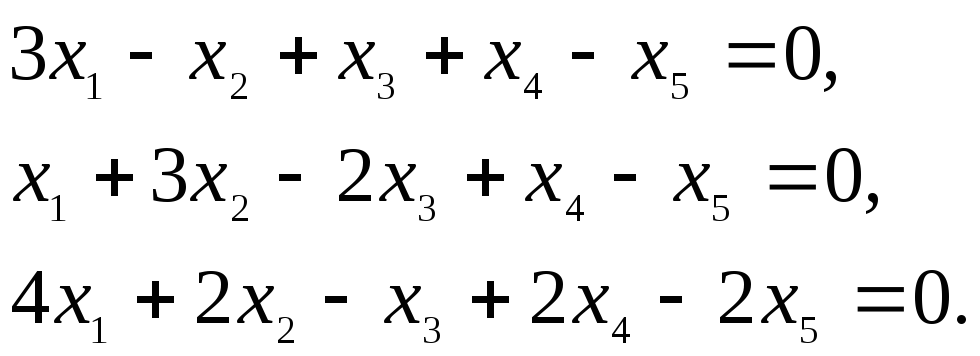
►Представленная система состоит из трёх уравнений и содержит 5 неизвестных. Выпишем матрицу системы и упростим её с помощью элементарных преобразований, сначала поменяв местами строки 1 и 2, а затем вычитая новую первую строку, умноженную на 3 и 4, соответственно из второй и третьей строк :

Видно, что ранг матрицы равен 2. Следовательно, две неизвестные являются главными, а три - свободными. Значит ФСР системы содержит 5-2=3 линейно независимых решения. Выберем в качестве главных. Это можно сделать, т.к. минор 2-го порядка, составленный из коэффициентов при этих неизвестных, отличен от нуля. Система, соответствующая преобразованной матрице, имеет вид

Отсюда, выражая главные неизвестные через свободные, получим общее решение

Или иначе:

.

Фундаментальная совокупность решений является базисом линейного пространства решений исходной системы и в данном случае имеет вид

Размерность искомого пространства равна 3.◄

Матрицей переходаот базисак базисуназывается матрица вида

где для каждого в -ом столбце стоят координатывекторав базисе.

Утверждение

Координаты векторав базисеи координатыэтого же вектора в базисесвязаны равенством

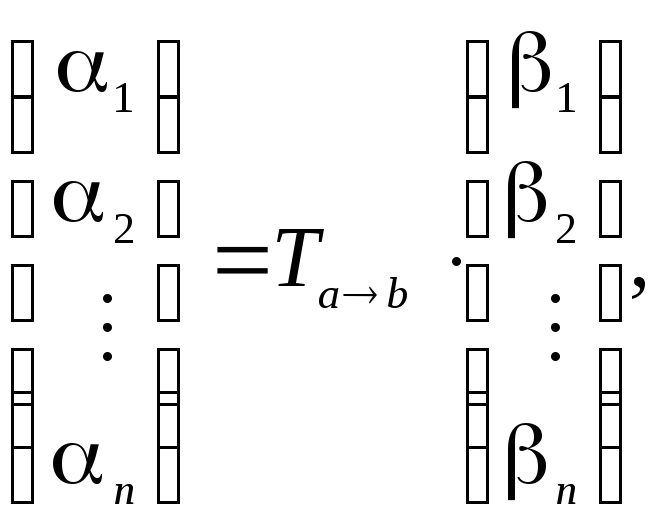
где - матрица перехода от базисак базису.

Утверждение. Матрица перехода от базисак бази­суи матрица обратного переходаот базисак базисусвязаны равенством=.

Типовые примеры

1.Найти координаты векторав базисе, если известно

►В соответствии с определением матрица перехода от базиса к базисуесть

.

Обозначим координаты вектора в базисечерез, а в базисечерез. Искомые координатысвязаны с известными координатамиследующим соотношением:

.

Видно, что для получения координат необходимо вычислить матрицу, обратную. Используя стандартную процедуру, имеем

.

Вычислим теперь координаты :

. ◄

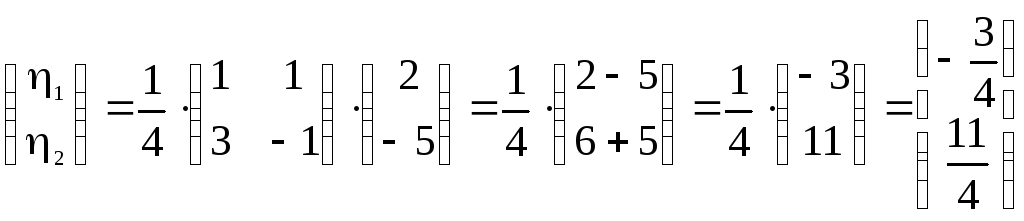2. Найти матрицу перехода от базиса 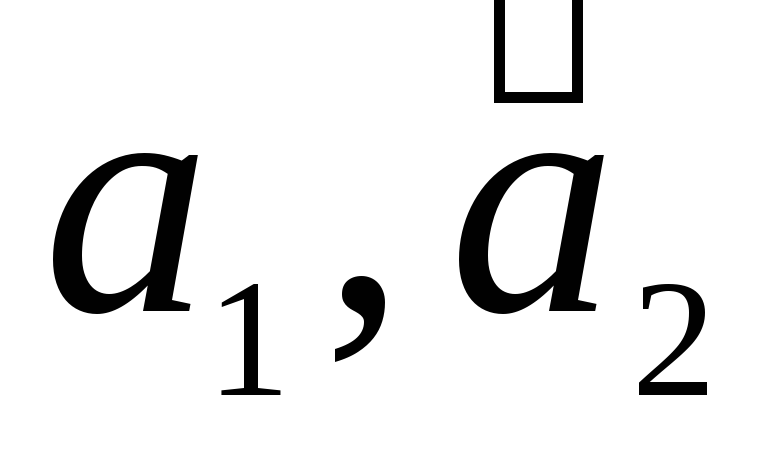к базису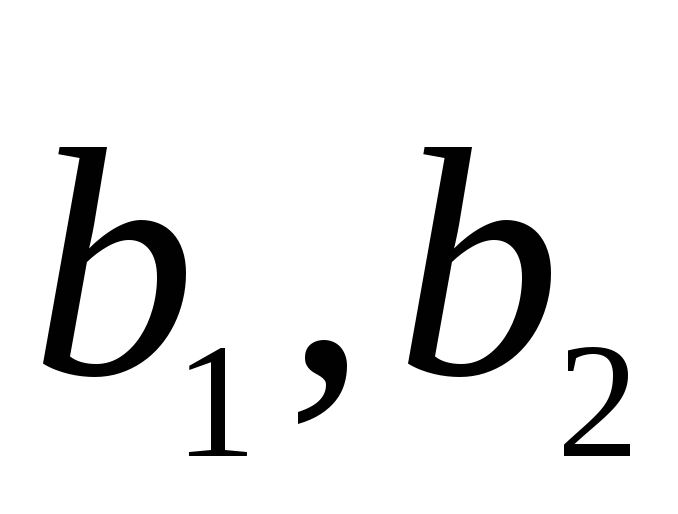по данным разложениям этих векторов в базисе:

.

►Чтобы построить матрицу перехода от базисак базису, необходимо найти разложение векторовпо базису. Сделаем это, представивв виде разложения пос неизвестными координатами, которые требуется определить:

,

или с учётом вида этих векторов в базисе

.

Откуда для координат имеем

Теперь, зная разложение по, выпишем матрицу:

.◄

5. Линейные оболочки и подпространства

Подпространством линейного пространстваназывается множество векторов изтакое, что для любых двух векторовиизи любых двух вещественных чиселилинейная комбинациятакже принадлежит.

Утверждение. Подпространство само является линейным про­странством.

Линейной оболочкойсистемы векторовназывается множество всех линейных комбинаций векторов. Обозначается.

Утверждение. Линейная оболочка системы векторов является подпространством.

Пересечениемдвух подпространстви на­зывается множество всех векторов, принадлежащих одновре­менно и, и . Обозначается .

Суммой двух подпространстви называется множество всех векторов, представимых в виде, где, . Обозначается .

Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством

+=+.

Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состо­ит только из нулевого вектора.

Типовой пример

Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами .

►Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства , порождённого векторами, равенство нулю линейной комбинации, эквивалентное системе уравнений, достигается лишь при условии. Следовательно, векторылинейно независимы и размерность подпространстваравна 2:. Для подпространства, порождённого векторами, проводя аналогичный анализ, получим.

Вычислим теперь размерность пересечения подпространств и. По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный векторподпространстваявляется линейной комбинацией базисных векторов:. Аналогично для подпространстваимеем, тогда условие принадлежности пересечению естьили.

Это условие представляет собой систему уравнений относительно коэффициентов . Составим матрицу системы и упростим её с помощью элементарных преобразований:

Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим ,

откуда .

Полагая свободное неизвестное , для остальных имеем

. Итак, пересечение подпространствимеет один базисный вектор

.

Размерность пересечения . Следовательно, в соответствии с равенством

размерность суммы подпространств . В качестве базиса суммы подпространств можно взять, например, векторы, дополненные вектором. В линейной независимости векторовубедиться нетрудно.◄