Глава 3. Линейные (векторные) пространства

§1. Понятие линейного пространства

1. Линейным (векторным) пространством называется множество элементов любой природы, если выполнены следующие три требования:

а) имеется правило, посредством которого любым двум элементам ставится в соответствие третий элемент этого множества, называемый суммой элементовии обозначаемый символом;

б) имеется правило, посредством которого любому элементу и любому числу() ставится в соответствие элемент этого множества, называемый произведением элементана числои обозначаемый символом;

в) для любых элементов и любых чиселивыполнены следующие аксиомы:

1. ;

2. ;

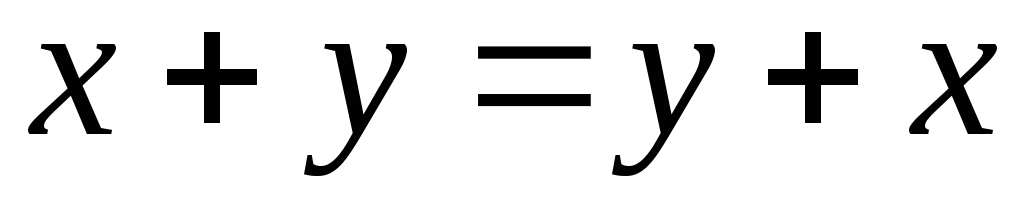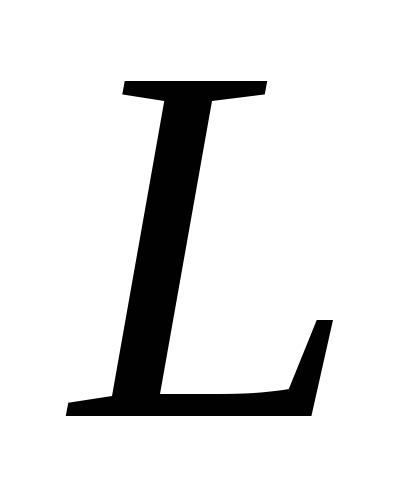3. . Этот элемент пространстваназывают нулевым (не путать с числом!);

4. . Такой элемент называют противоположным для;

5. ;

6. ;

7. ;

8. .

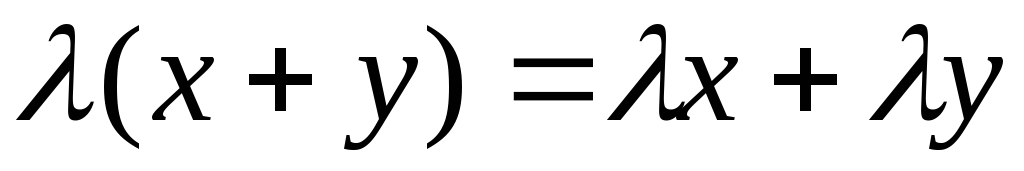Замечание 1. Если в пункте II мы ограничиваемся вещественными числами, то называется вещественным векторным пространством; если же определено умножение на любое комплексное число, то векторное пространство называется комплексным.

Замечание 2. Элементы произвольного векторного пространства принято называть векторами. То обстоятельство, что часто термин «вектор» употребляется в более узком смысле, при этом не приводит к недоразумениям, а, напротив, обращаясь к сложившимся геометрическим представлениям, можно уяснить, а зачастую и предвидеть ряд результатов, справедливых для векторных пространств произвольной природы.

При введении понятия векторного пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов и произведения элемента на число. Важно лишь, чтобы эти правила удовлетворяли аксиомам векторного пространства.

Примеры векторных пространств.

1. Пространство векторов на плоскости.

2. Пространство векторов в трехмерном пространстве.

3. Множество многочленов с вещественными коэффициентами степени не вышеобразует векторное пространство относительно операций сложения многочленов и умножения многочлена на вещественное число.

4. Множество матриц одинаковых размеров образуют векторное пространство относительно операций сложения матриц и умножения матрицы на число. В частности, часто встречается и используется векторное пространство матриц-строк(). Для него принято другое обозначение –(). Элементами этого векторного пространства служат упорядоченные совокупностипроизвольных вещественных (комплексных) чисел.

5. «Нестандартный» типовой пример. Рассмотрим множество всех положительных вещественных чисел. Определим «сумму» двух элементовкак произведение вещественных чисели(понимаемое в обычном смысле):. «Произведение» элементана вещественное числоопределим как возведение числав степень:. Нулевым элементом пространства будет служить вещественное число, а противоположным элементом (для данного элемента) будет число. Проверьте выполнение аксиом векторного пространства (которые в обычной записи принимают другой вид: вместомы имееми т.д.). В этом Типовой примере, быть может, для обозначения суммы элементов пространства и для произведения элемента пространства на число предпочтительнее другие обозначения (например,и).

Арифметическим пространством Rⁿ называется множество векторов , в котором операции сложения векторов и умножения вектора на число определены следующим образом: если,,, то

,.

Утверждение

Множество всех решений однородной системы об­разует

линейное пространство.

2. Некоторые свойства произвольных векторных пространств. Из определения векторного пространства следует ряд утверждений, справедливых для произвольных векторных пространств.

1. В векторном пространстве существует единственный нулевой элемент.

2. Для каждого элемента векторного пространства существует единственный противоположный элемент.

3. .

4. Для любого элемента противоположный ему элементравен произведению элементана число, т.е..

Отметим также, что из определения векторного пространства следует существование и единственность разности любых двух элементов векторного пространства и, которая определяется как элемент, удовлетворяющий условию. Этим элементом служит сумма.