§4. Теорема Гаусса в дифференциальной форме. Уравнения Пуассона и Лапласа

Запишем соотношение (2.7) выражающее теорему Гаусса

. (4.1)

Из векторного анализа известна теорема Остроградского–Гаусса, которая связывает поток какого-либо вектора через замкнутую поверхность с дивергенцией этого вектора, проинтегрированной по объему, заключенному внутри этой поверхности:

. (4.2)

Напомним, что дивергенция вектора Е:

.

Сравнивая уравнения (4.1) и (4.2) можно заключить, что

. (4.3)

Соотношение (4.3) представляет собой теорему Гаусса в дифференциальной форме и является одним из фундаментальных уравнений электродинамики.

Проведем вывод уравнения (4.3) без ссылки на теорему Остроградского-Гаусса (4.2). Пусть в пространстве распределен электрический заряд с плотностью(x,y,z). Выделим мысленно бесконечно малый элемент объема в виде параллелепипеда, ребра которого параллельны координатным осям и равныdx, dy, dzсоответственно.

Суммарный поток dФ_хчерез две грани, перпендикулярные осих, равен

.

Аналогичным образом определяются потоки dФ_y и dФ_zчерез грани, перпендикулярные осям y и z, соответственно.

Полный поток вектора Ечерез поверхность бесконечно малого параллелепипеда равен

. (4.4)

Соотношение (4.4) представляет теорему Остроградского-Гаусса (4.2) для бесконечно малого объема.

Согласно теореме Гаусса (2.7) поток dФвектораЕчерез поверхность бесконечно малого параллелепипеда равен заряду в объеме, ограниченном этой поверхностью, деленному на₀.

. (4.5)

Сравнивая (4.4) и (4.5) получаем (4.3).

Выразим Ечерез градиент потенциала

и подставим в (4.3)

.

Оператор называется оператором Лапласа.

Уравнение

(4.6)

называется уравнением Пуассона. В принципе, его можно решить при любом заданном распределении заряда(x,y,z).

В свободном пространстве правая часть уравнения (4.6) равна нулю, и мы получаем уравнение Лапласа:

. (4.7)

Уравнение Лапласа относится к числу основных уравнений математической физики.

Помимо самих уравнений Лапласа и Пуассона принципиальную важность имеют условия на границах той области, для которой ищется решение (граничные условия). Ими обычно и определяется физическая постановка задачи.

В дальнейшем мы рассмотрим граничные условия на поверхности проводников и диэлектриков.

§5. Электрический диполь. Поле диполя

Э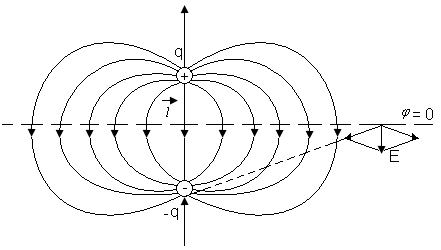лектрическим диполем называют систему из двух зарядов +qи –q, на расстоянииlдруг от друга. Прямая, проходящая через оба заряда, называется осью диполя.

Величина называется вектором дипольного момента, при этом векторl направлен от отрицательного заряда к положительному.

Найдем потенциал и напряженность электрического поля диполя.

Потенциал, создаваемый зарядами + qи –qв точке, находящейся на расстоянииRот положительного заряда +qи на расстоянии |R+l| от отрицательного заряда –qравен

. (5.1)

Расстояние |R+l| найдем по теореме косинусов (угол между векторомRи осью диполя).

. (5.2)

Будем рассматривать расстояния Rзначительно превышающие расстояниеlмежду зарядами () и использоватьдипольное приближение, в котором пренебрегается слагаемыми, содержащими (l/R)²по сравнению с (l/R).

Тогда можно приближенно считать

Пользуясь тем, что при , можно заменить, получим

.

Так как , то потенциал поля, создаваемого точечным диполем.

. (5.3)

Отметим, что если начало радиус-вектора Rпоместить в точку, где находится заряд –q, или в любую другую точку между зарядами, в дипольном приближении выражение для потенциала (5.3) не изменится.

Зная потенциал как функцию координат, можно найти напряженность Е.

Таким образом

. (5.4)

Как видно из (5.3) и (5.4), потенциал поля диполя пропорционален R^-2, а напряженность пропорциональнаR^-3. При этом, в отличие от точечного заряда, поле зависит от угла между радиусом и осью диполя.