1.3. Погрешности измерения физической величины

Истинное значение исследуемой физической величины экспериментально с помощью технических средств измерений определить невозможно. Всегда существует разница _Х между ее измеренным Х и истинным Х_и значениями

_Х = Х - Х_и,

величина которой определяется уровнем развития экспериментальной базы, совершенством методики измерения и суммой знаний об исследуемом объекте. Эта разница _Х называется погрешностью измерения физической величины.

Отсюда следует, что истинное значение физической величины в реальных условиях знать практически невозможно, поэтому в любом эксперименте при определении погрешности получения измерительной информации вместо нее принято использовать, так называемое, действительное значение Х_д измеряемой величины Х, т.е. искомую физическую величину определенную экспериментально с наивысшей точностью ^*.

Признание того, что информация, полученная экспериментальным путем, неизбежно содержит ту или иную ошибку, заставляет нас придерживаться правил, неукоснительное следование которым лежит в основе грамотности и профессионализма экспериментатора (неважно физика, химика, инженера и т. п.):

1) численное значение экспериментально полученной физической величины должно обязательно сопровождаться указанием величины возможной ошибки и если эта ошибка случайная вероятности ее проявления (доверительной вероятности или коэффициента надежности), с которой измеряемая величина попадает в диапазон, определяемый величиной указанной погрешности. Без такой информации о точности измере­ния его результат бесполезен;

2) единичные измерения недопустимы, достоверность измерительной информации, полученной в результате единичного измерения, должна обязательно проверяться на наличие грубых ошибок (промахов) путем проведения повторных измерений. На практике, если экспериментатор полностью доверяет измерительному устройству (установке), как правило, делается одно измерение. Основываясь на своем опыте и знании исследуемого явления, экспериментатор решает вопрос о необходимости повторения эксперимента. Если исследуемый процесс неизвестен, то для исключения грубой ошибки (промаха) проводится повторное измерение, точнее два измерения, которые позволят принять правильное решение.

О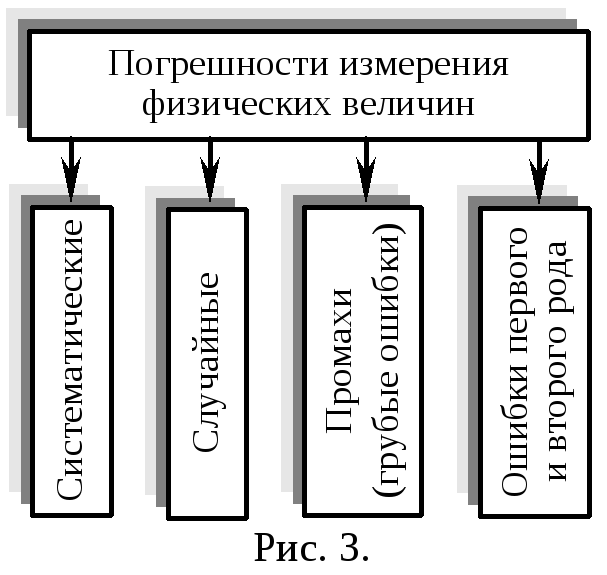тдельные, единичные измерения, не подтвержденные повторными измерениями, принято называтьнаблюдениями.

1.3.1. Виды погрешностей измерения физических величин

1.3.1.1. Классификация погрешностей по закономерности проявления

Погрешности измерения физических величин _Х всегда содержат систематическую и случайную составляющие (рис. 3), которые существуют совместно, внося то или иной вклад в общую величину ошибки. Первая составляющая получила название систематической _с погрешности, вторая случайной _сл погрешности.

Систематическая погрешность _с – это составляющая общей погрешности измерения физической величины, остающаяся постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины в одних и тех же условиях.

Пример:Погрешность градуировки измерительного прибора или погрешность влияния внешних факторов (например, температуры, давления, влажности и т.п.).

Анализ источников систематических погрешностей - одна из основных задач при точных измерениях. Как правило, найденная систематическая погрешность может быть исключена из результата измерения путем введения соответствующей поправки.

Случайная погрешность _сл – составляющая общей погрешности измерения, изменяющаяся случайным образом без видимой закономерности при повторных измерениях одной и той же величины в одних и тех же условиях. Случайные погрешности являются следствием наложения случайных процессов, сопровождающих любое физическое измерение и влияющих на его результат.

Случайную погрешность полностью нельзя исключить опытным путем. Случайную погрешность, в отличие от систематической, можно уменьшить до минимума путем многократных измерений одной и той же величины в одинаковых условиях. Наиболее достоверное значение измеряемой величины, полученное на основе многократных измерений – среднее арифметическое из ряда полученных измерений

, (7) .

где X₁,…, X_n – результаты отдельных измерений, а n – число измерений.

Систематические и случайные ошибки связаны между собой. Существует возможность построения эксперимента таким образом, что постоянный фактор, влияющий на результат измерений, в каждом из них действует разным образом, т.е. при необходимости систематическая ошибка может быть переведена в случайную. Этот прием используется при минимизации ошибок получения измерительной информации и носит название рандомизации. Рандомизация на практике позволяет исключать многие неизвестные систематические ошибки^*.

Особый вид ошибок это грубые ошибки (или промахи) - они возникают в результате невнимательности экспериментатора при отсчете по прибору, записи результатов, неправильном включении или расположении прибора.

Способ устранения грубых ошибок - правильное планирование эксперимента, внимательная и аккуратная работа при его проведении. Для устранения возможности появления промаха измерения в процессе выполнения эксперимента необходимо проводить несколько раз. Обнаруженные промахи следует всегда исключать из рассмотрения при обработке результатов измерений.

Ошибки первого и второго рода это специфический вид ошибок, как правило, возникающий при определении качества готовой продукции (при приемо-сдаточных испытаниях или разбраковке больших партий готовой продукции). Задача измерений контролируемой величины состоит в этом случае не в получении точного ее значения, а в необходимости определения утвержденного Техническими условиями (ТУ) параметра для которого определены допуски, установленные для данной продукции. Если измеренный параметр укладывается в эти допуски, изделие принято относить к годному, если не укладывается - к браку. Следствием таких ошибок измерений могут быть два результата: 1) хорошее изделие бракуется и 2) бракованное изделие считается годным. В первом случае мы делаем ошибку первого рода, во втором – ошибку второго рода.

Пример:Провести оценку качества (разбраковку) постоянных магнитов по величине индукции на торцевой поверхности. Интервал допустимых значений индукции на поверхности постоянного магнита 110 - 120 мТл. Класс точности измерителя магнитной индукции 1,5. При измерении на пределе 150 мТл абсолютная погрешность  не превышает 2,3 мТл.

При измерении получена величина 121,8 мТл. Мы бракуем этот магнит, хотя в действительности при данной точности измерений, нормируемая величина может находиться внутри интервала допустимых значений (121,8 – 2,3 = 119,5 мТл). Если мы бракуем годное изделие, мы совершаем ошибку первого рода.

Наоборот, если при той же точности измерений оказалось, что индукция на поверхности постоянного магнита 119,5 мТл., мы признаем этот магнит годным, хотя он мог иметь индукцию на поверхности 119,5 + 2,3 = 121,8 мТл, т.е. должен был считаться браком. В случае, когда годным признается бракованное изделие, мы совершаем ошибку второго рода.

Из сказанного выше ясно, что ошибку первого или второго рода сделать легче всего, когда измеряемая величина лежит вблизи границы интервала допустимых значений. Казалось бы, что наиболее неприятна ошибка второго рода - пропуск брака, однако это зависит от степени ответственности за качество изделия. Необходимо учитывать что выгоднее либо отбраковка некоторого количества годных изделий, либо возможность попадания в годные изделия некоторого количества, со свойствами хотя и меньшими, но близкими к граничным значениям. Поэтому при выборе системы измерений и отбраковки соображения экономической целесообразности во всех случаях являются важными.

Иногда бывает достаточным знание приближенного значения измеряемой величины, полученного по показаниям того или иного прибора. Если этого недостаточно и необходимо определение ее значения, приближающегося к истинному (обеспечение высокой точности результата), проводят обработку результатов наблюдений. Принято степень близости действительного значения измеренной физической величины к истинному ее значению оценивать с позиции теории вероятностей. Разработаны вероятностные методы оценки погрешности результатов измерений на основании ряда наблюдений [4].