4. Пример расчета плоской размерной цепи с параллельными линейными размерами

4.1. Исходные данные

4.1.1. Задача расчета

Рассчитать допуски на составляющие звенья размерной цепи, обеспечивающие величину зазора между торцом втулки (поз. 6) и подшипником (поз. 1) подшипниковой опоры конической передачи (рис. 2) в пределах от 0,1 до 0,4 мм. Расчеты провести методами полной взаимозаменяемости, неполной взаимозаменяемости и регулирования.

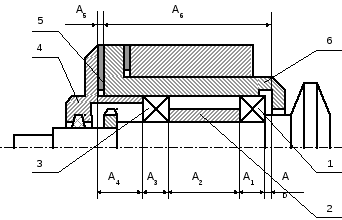
Рис. 2. Эскиз подшипниковой опоры конической передачи

4.1.2. Условия расчета

Средне-экономическую точность обработки деталей - звеньев размерной цепи принять по IT11.

При расчете вероятностным методом принять для всех составляющих звеньев размерной цепи относительное среднее квадратическое отклонение , коэффициент асимметрии кривой распределения _i=0, а риск Р=0,27%.

4.1.3 Расчет параметров исходного звена.

4.1.4. Составление эскиза сборочной единицы (рис. 2) и выявление, используя эскизы деталей (рис. 3), составляющих звеньев размерной цепи (табл. исх. данных).

Рис. 3. Эскизы деталей подшипниковой опоры конической передачи:

а) – втулка, б) – крышка, в) – стакан

4.1.5. Составление схемы размерной цепи и таблицы исходных данных

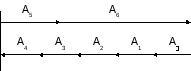
Таблица 1

Исходные данные для расчета размерной цепи

Обозначение состав-ляющего звена раз-мерной цепи	Наименование детали по специификации	Звено отнесено к отвер-стию или валу	Передаточное отношение 	Размеры стандартных со-ставляющих звеньев	Номинальные размеры по заданному варианту, мм	Номинальные размеры, округленные по ГОСТ 6636-69, мм	Единица допуска i, мкм
А	Исход-ное звено	–	–	–		–	–
А1 l1	Под-шипник	–	-1	18+0,1	–	–	1,08
А l2	Втулка	Вал	-1	–	140	140	2,52
А l3	Под-шипник	–	-1	18+0,1	–	–	1,08
А4 l4	Крыш-ка	Отв.	-1	–	27	24	1,31
А l5	Про-кладка	Вал	+1	–	0	0	–
А l9	Стакан	Вал	+1	–	200	200	2,9

Примечание: знак по гост 2.304-81 читается как «соответствует».

Единица допуска постоянна для каждого из интервалов размеров и определяется из прил.1. табл. 3.

4.1.6. Составление уравнения номинальных размеров

А_=А_+А_-А_-А_-А_-А₄

4.2. Решение прямой задачи методом полной взаимозаменяемости (расчеты ведутся методом максимума-минимума).

4.2.1. Решение уравнения номинальных размеров

Подставляя номинальные размеры составляющих звеньев размерной цепи по заданному варианту, получаем:

A_ = 200 – 27 – 18 – 18 – 140 = -3 мм.

Проверяем соответствие номинальных размеров составляющих звеньев рядам линейных размеров по ГОСТ 6636-69 (прил. 1, табл. 4). Размер А₄ l₄ = 27 мм не является стандартным. За счет этого размера, приняв стандартное значение А₄=24 мм, можно достичь требуемого A_ = 0.

A_= 200 – 24 – 18 – 18 – 140 = 0 мм.

4.2.2. Расчет допусков составляющих звеньев размерной цепи

Определим квалитет, одинаковый для всех составляющих звеньев:

По табл. 1 (прил. 1) принимаем 7 квалитет, для которого к =16.

Назначаем допуски по табл. 1, прил. 5 на все составляющие звенья по IT7 (кроме звеньев с заранее заданными допусками и звена А₆, принимаемого в качестве специального звена):

ТА₁ = 0,1 мм (задан);

ТА₂ = 0,040 мм;

ТА₃ = 0,1 мм (задан);

ТА₄ = 0,021 мм;

ТА₆ = ТА_{6 сп} = ?.

Определяем расчетный допуск на специальное звено:

Ближайший (меньший) стандартный допуск по по табл. 5 (прил. 1) IT6=0,029 мм, таким образом, для дальнейших расчетов принимаем ТА_{6 сп}=0,029 мм.

4.2.3. Определение предельных отклонений

Назначаем предельные отклонения на все размеры составляющих звеньев размерной цепи (кроме специального звена) как на основные валы или отверстия соответственно по h7 и H7:

А₁=18^+0,1 (задан);

А₂=140_-0,040;

А₃= 18^+0,1 (задан);

А₄=24^+0,021;

А₆= А_{6 сп}=?.

Определяем координаты середин полей допусков замыкающего и составляющих звеньев размерной цепи:

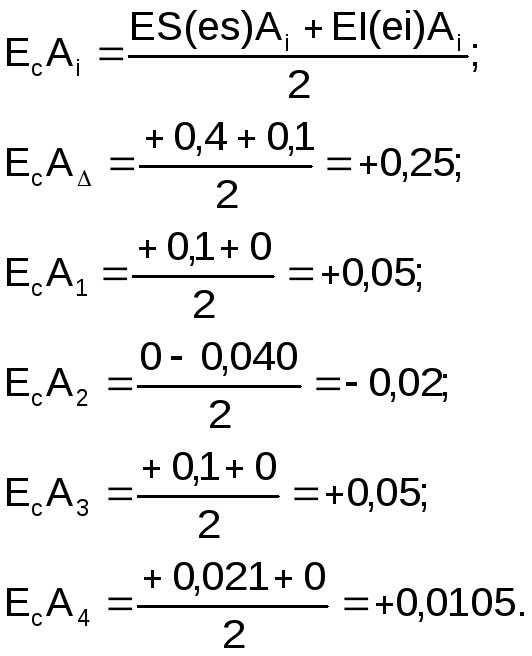
Определяем координату середины поля допуска специального звена:

Определяем предельные отклонения специального звена:

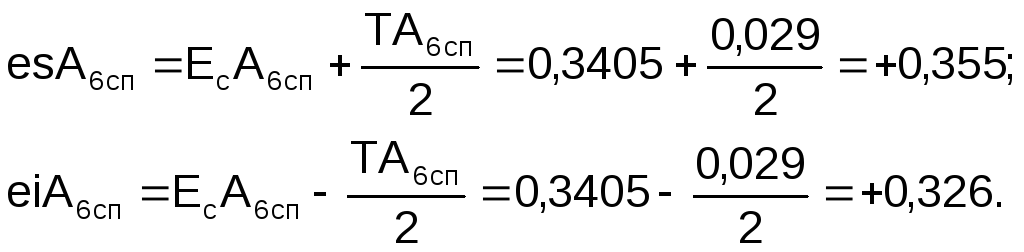
Таким образом, расчетное значение специального звена: .

Подбираем ближайшее стандартное значение основного отклонения специального звена. Расчетное основное отклонение специального звена – нижнее eiА_{6 сп}=+326 мкм. По таблице числовых значений основных отклонений ГОСТ 25346-89 (прил.1, табл. 6) выбираем два стандартных основных отклонения (так как расчетное значение расположено примерно посередине): v (eiА_{6 сп}=+284 мкм) – меньше расчетного и x (eiА_{6 сп}=+350 мкм) – больше расчетного.

Второе предельное отклонение рассчитываем по формуле

esА_{6 сп}=eiА_{6 сп}+ТА_{6 сп}.

Таким же образом далее рассматриваем два варианта стандартных значений специального звена:

Вариант І

Вариант ІІ