Мухамедзянов ТЛЭЦ / раздел 3 / 3-2

3.1.2 Свойства функций реактивных двухполюсников

Исследование функций Z и Y проводят с использованием следующих свойств:

1. Общее число нулей и полюсов на единицу больше числа элементов, число резонансов на единицу меньше числа элементов.

2. Нули и полюса функции Z , Y строго чередуются.

3. Функции Z, Y могут иметь асимптоты: вертикальную ось, горизонтальные асимптоты, наклонные асимптоты типа jωL_э.

4. Производная по частоте от сопротивления положитеоьна.

3.1.3 Формула Фостора

Формула Фостора позволяет нам записать аналитическое выражение Z двухполюсника без вывода

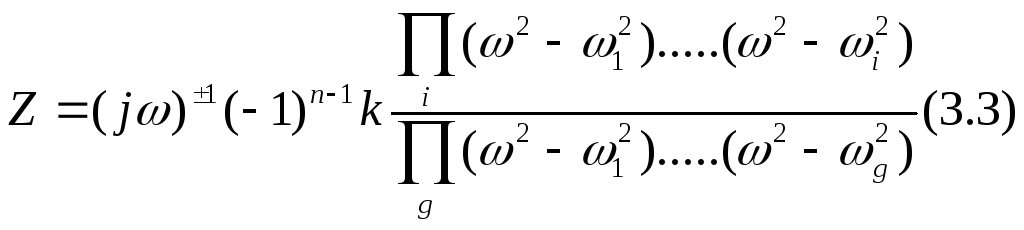
Примечание: +1 если схема пропускает постоянный ток и наоборот, n-1 число резонансов.

k- определяется следующим образом:

Коэффициент К определяется при ω=∞ путем разрыва индуктивностей, к. з. некоторых емкостей, но так чтобы цепь не размыкалась.

3.1.4 Обратные Двухполюсники

Обратные двухполюсники – такие Д у которых произведение сопротивлений Z₁*Z₂ на всех частотах величина постоянна Z₁*Z₂=R²=const (3.4)

Потенциально обратные двухполюсники таковы , что при изменении величин элементов одной из схем (без изменения самих схем) они станут обратными.

Они должны иметь противоположный характер Z при ω=0 и при ω→∞.

Рассмотрим расчет элементов обратного двухполюсника (На примере схем 1,3 в разделе 3.1.3):

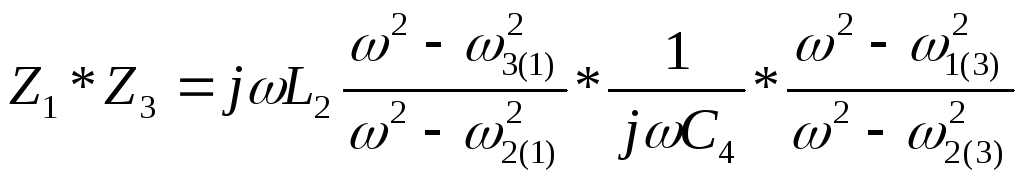
Последняя система определяет какими должны быт элементы схемы 1 чтобы быть обратной схеме 3.

Отсюда вытекают условия обратности схем:

(3.5)

3.1.5 Эквивалентный двухполюсники.

Эквивалентный двухполюсники такие что: Z₁=Z₂ на всех частотах.

Потенциально эквивалентные двухполюсники – такие, которые при изменении величин элементов одной схемы становятся эквивалентными.

Эквивалентные двухполюсники должны удовлетворять двум условиям:

1. Иметь одинаковое сопротивление при всех частотах.

2. Иметь одинаковый характер Z при ω→∞.

Рассмотрим на примере На примере схем 1,2 из разделе 3.1.3

где

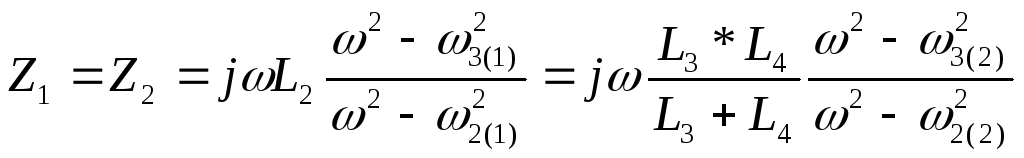
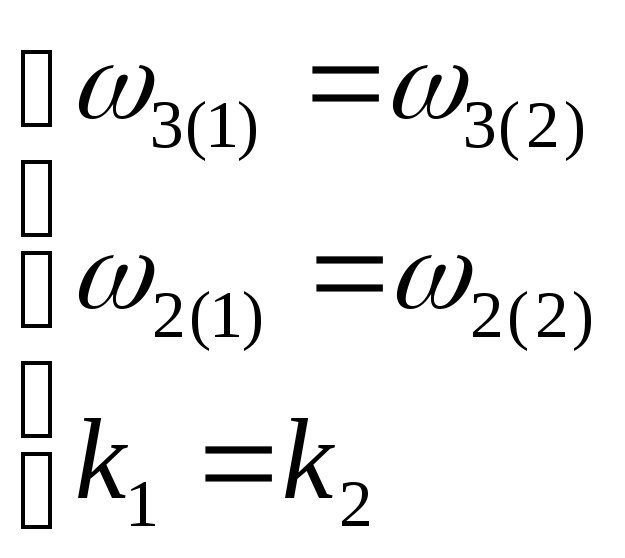(3.6) раскроем эту систему:

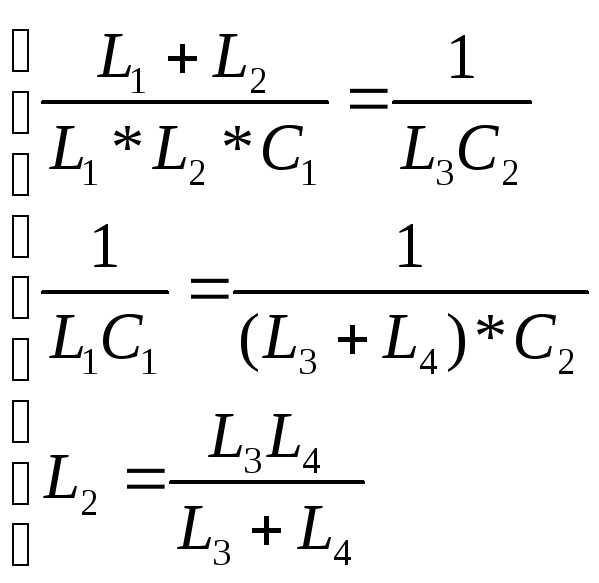
Последняя система определяет какими должны быт элементы схемы 1 чтобы быть эквивалентной схеме 2.

Система 3.6 –условия эквивалентности.

3.1.6 Сокращаемые Элементы двухполюсников.

Сокращаемые Элементы – такие элементы, добавление которых в схему не изменяет числа резонансов схемы.

Выявить являются те или иные элементы сокращаемыми или нет можно двумя способами:

1). Написать аналитическое выражение Z(P) или Z(ω) приравнять числитель и знаменатель, т.е. выяснить число резонансов и сравнить с числом элементов.

2). Графически построить зависимость сопротивления от частоты, выяснить число резонансов и сравнить с числом элементов.

Пример:

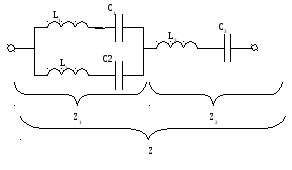
Возникло подозрение не являются ли элементы L₃ и C₃ сокращающимися.

Построим график.

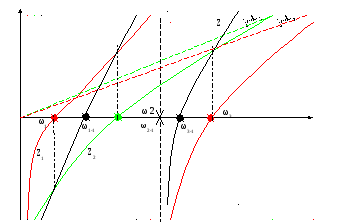
Из графика видно что он дважды пересекает ось Z=0 т.е. имеет два резонанса токов, соответственно данную схему можно представить в виде схемы имеющей 4 элемента.

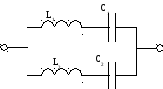
Добавление L_3, C₃ не изменило общего числа резонансов, а привело к сдвигу резонансов напряжений.

3.1.7 Синтез двухполюсников

Свойства входных функций

Критерии физической реализуемости

Предположим, что a_n ф-ии входного типа тогда:

Или в операторной форме:

(3.7)

A(P)

B(P)

A(P), B(P)- полиномы

Z(P) можно представить в виде:

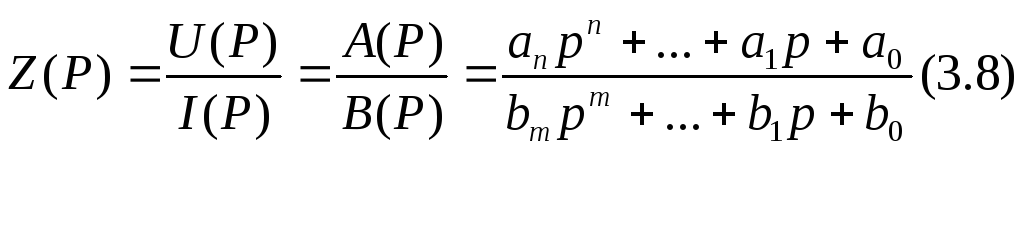
Каким условиям должна удовлетворять функциям 4.10, чтобы быть реализованной в виде схемы.

При ω→∞ чисто реактивное сопротивление ведет себя:

Следовательно

1). Высшая степень переменной числителя и высшая степень переменной знаменателя отличаются на 1

2). Критерии :все коэффициенты полиномов положительны и вещественны

3). Нули и полюса Z(P) находятся в левой полуплоскости комплексной частоты.

4). Нули и полюса Z(P) должны быть некратными, простыми.

5). Нули и полюса строго чередубтся.

3.1.8 Синтез по Фостеру.

Первая формула.

Дано аналитическое выражение Z(jω) – Z(P)

Требуется определить схему и величины элементов.

Первое : проверяем выражение по критериям физической реализуемости .

Второе: Задаемся следующей схемой:

Третье: Решаем заданное выражение

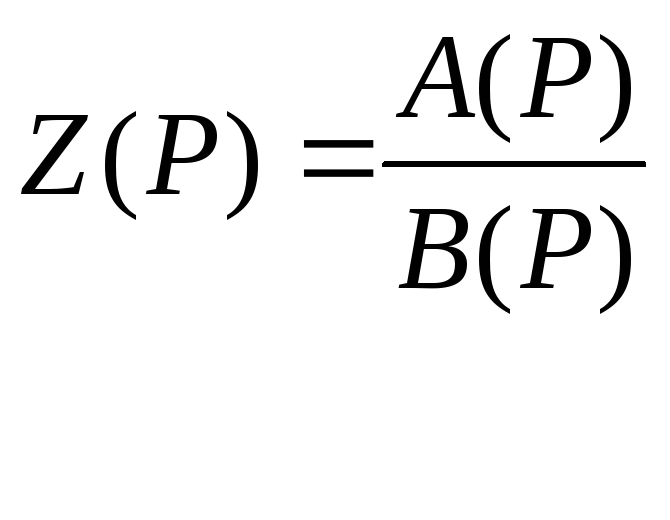, решая уравнение A(P)=0, находим нули решая B(P)=0.

Находим полюса Z(P).

Для определения величин элементов моно и не находить нули Z(P), достаточно найти полюса, т.к. такая функция полностью определяется вычитаниями полюсов.

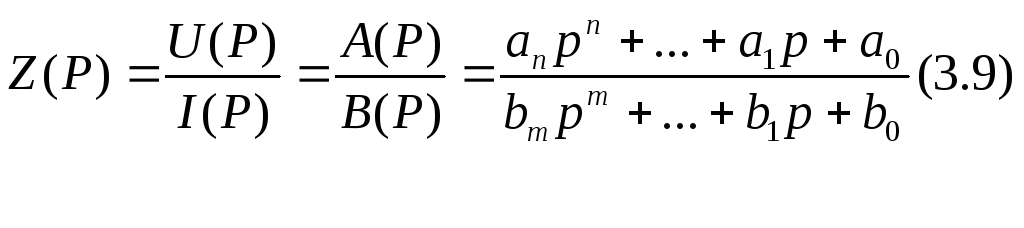Величина Z(P) при P→∞ стремится к pL₀.

Если от заданного аналитического выражения определить lim_P→∞ то этот дает L₀ в полюсе бесконечности.

Со определяет поведение Z(P) при P→0. Необходимость нахождения L₀ и Со обявлялась в пункте (3.1.1).

При

3.1.9 Синтез по второй формуле Фостера.

1). Проверяем выражение по критериям физической реализуемости.

2). Задаемся схемой:

3). В данном случае удобнее работать с проводимостью:

При A(P)=0 – находим все полюса Z(P)

Если в точке ω=0 есть полюс то есть С₀

При ω→0

3.1.10 Реализация по Кауэру.

(Схемы Кауэра)

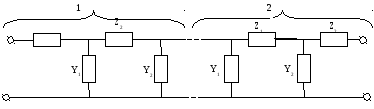
Запишем Z(P) и Y(P) соответственно для первой и второй схем.

1. 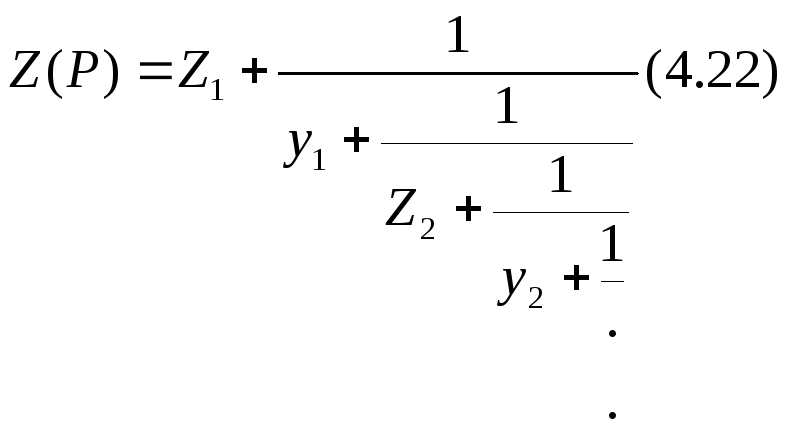2.

На элементной базе они будут выглядеть следующим образом.

1.

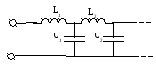
Найдем Z, K=L₁ тогда,

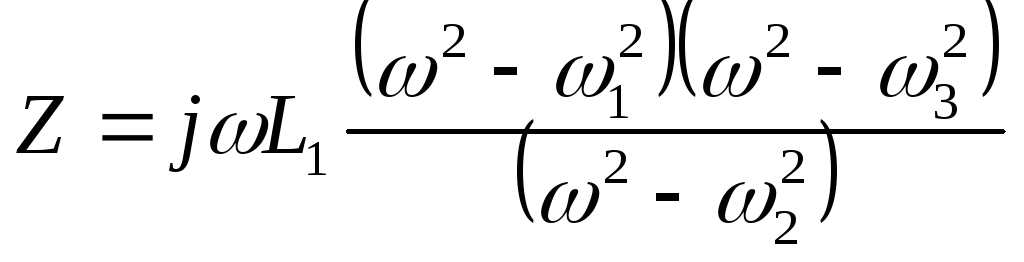
Пусть задано Z(P) выясним, что удовлетворяет ли оно преобразуемого по формуле Кауэра Запишем полиномы A(P) и B(P) по убывающим степеням. Последовательно делим числитель и знаменатель с понижением степени переменной так чтобы в конце получился 0. Получаем что степень числителя больше степени знаменателя.

1

A₁(P)

y₁

). 2). 3). И так далее.

Для второго случая.

Если в аналитическом выражении Z(P) старшая степень полинома В выше старшей

Степени полинома А то первое деление будет и результат первого деления будет Y₁ и схема будет выглядеть следующим образом:

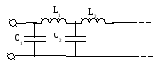
3.2. Двухполюсник с потерями.

При Z=R+jX придется рисовать два графика: Фазовый и сопротивлдений.

Цепи первого порядка (одноэлементные двухполюсники)

1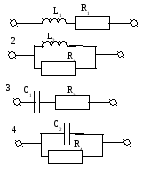

Основной характеристикой двухполюсника является частотное характеристика.

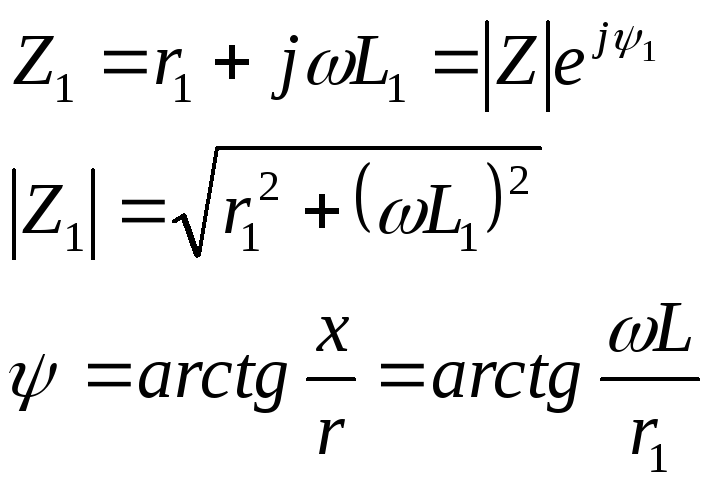
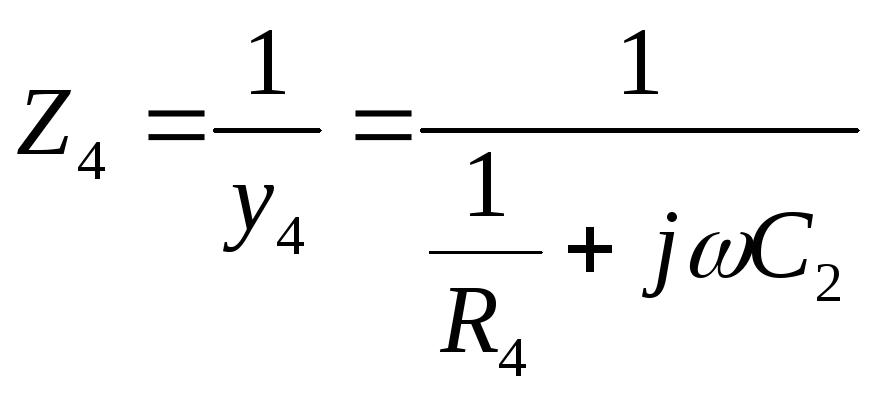
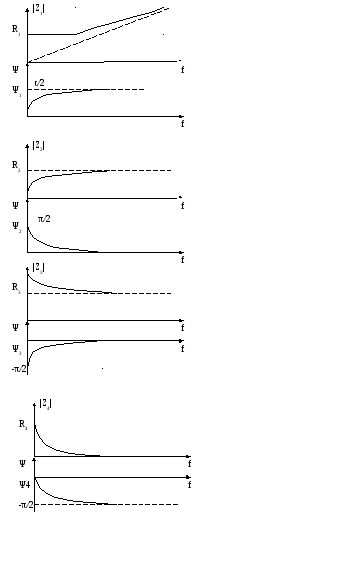
3.2.1 Двух элементный двухполюсник.

Последовательный контур.

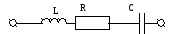
Параллельный Контур.

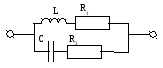
Re(y)

Im(y)

При резонансе Im(y)=0 т.е.

По формуле 3.15 делаем вывод:

1. Значение резонансной частоты зависит не только от величины реактивных элементов но и от активных сопротивлений.

2. При определении соотношениях параметров схемы резонансов нет мнимых резонансов.

Условия Резонансов:

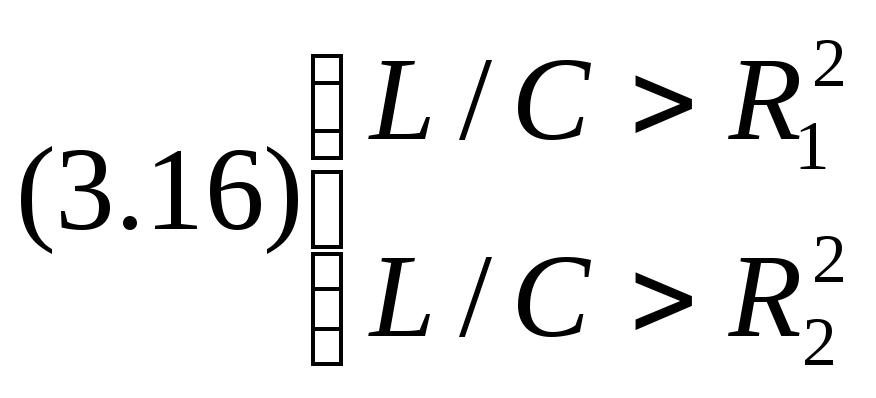
Примем в случае 3.17 резонансные св-ва выявлены слабо.

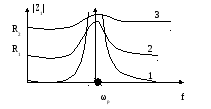
1. идеальная.

2. R₁<R₂

Для характеристики колебательной системы вводится понятие добротности.

(3.18)

При резонансе ω_РL=1/ ω_РC (3.19)

p- характеристическое сопротивление контура.

, например Q₂>Q₃

Кроме этого вводится понятие полосы пропускания

Полоса пропускания – это полоса частот в которых мощность снижается не более чем в два раза.

3.2.2 Использование колебательных систем в качестве фильтрующих цепей.

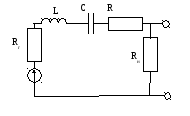
Такой контур будет давать сигналы близкие к резонансной частоте.

Степень подавления помехи :

Чем выше добротность контура тем лучше его избирательные свойства.

Здесь получаемые противоречия между требуемой полосой пропускания и избирательностью. Увеличение Q приводит к увеличению S, а с другой стороны уменьшает полосу пропускания. Полоса пропускания может оказаться уже чем требуется, что приведет к амплитудно-частотным искажениям. Следовательно необходимо улучшить прямоугольность АЧХ.