
- •1. Основы метрологии
- •Основные статьи фз рф «Об оеи» устанавливают:
- •Поверка средств измерений
- •Виды поверок:
- •Эталоны
- •Международная система единиц физических величин (си, si)
- •Преимущества системы si
- •Эталоны основных физических величин
- •Методы измерений
- •Классификация методов измерений
- •1. По характеру зависимости измеряемой величины от времени:
- •Классификация средств измерений
- •Метрологические характеристики средств измерений
- •Погрешности средств измерений
- •Классы точности средств измерений
- •Причины возникновения погрешностей измерения
Причины возникновения погрешностей измерения
Погрешности средств измерения.
Погрешности, зависящие от установочных мер.
Погрешности, зависящие от измерительного усилия.
Погрешности, происходящие от температурных деформаций
Погрешности, зависящие от оператора (субъективные погрешности):
погрешность отсчитывания;
погрешность присутствия (теплоизлучения оператора);
погрешность действия (вносится оператором при настройке прибора);
профессиональные погрешности.
6. Погрешности при отклонениях от правильной геометрической формы.
7. Дополнительные погрешности при измерении внутренних размеров.
Случайные погрешности измерений
Неизбежны при измерении и нет определенных закономерностей их проявления.
Случайные погрешности можно обнаружить только при многократных измерениях.
На практике случайные погрешности подчиняются закону нормального распределения: когда большинство результатов близки к номинальному размеру и лишь отдельные результаты существенно отличаются. Кривая, описывающая эти частоты, называется кривой нормального распределения, ее описывает математическое выражение:
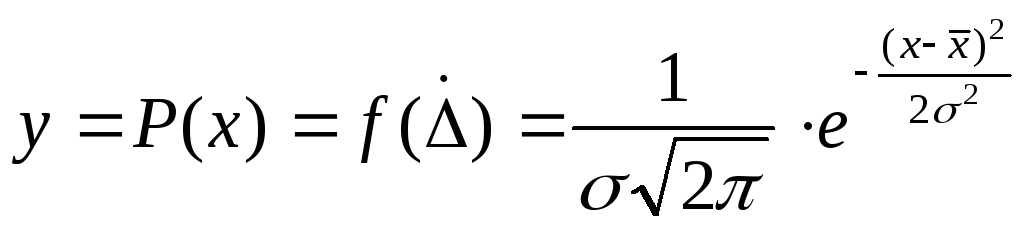
![]() -
среднеквадратичное отклонение (СКО);
-
среднеквадратичное отклонение (СКО);
![]() -
независимая переменная величина;
-
независимая переменная величина;
![]() -
плотность вероятности
-
плотность вероятности
![]() -
среднее арифметическое значение
(математическое ожидание случайной
величины)
-
среднее арифметическое значение
(математическое ожидание случайной
величины)
![]()
![]() -
основание натурального логарифма.
-
основание натурального логарифма.
![]()
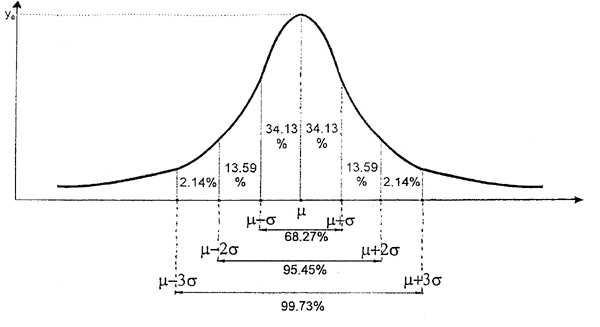
Нормальное
распределение определяется двумя
параметрами:
![]() и
и![]() ,
зная их можно задать нормальное
распределение:
,
зная их можно задать нормальное
распределение:
![]() ;
;
![]()
Среднее – арифметическое ряда значений:
![]()
Дисперсия (рассеивание), на практике берут СКО Погрешность среднего арифметического значения единичного результата измерений:
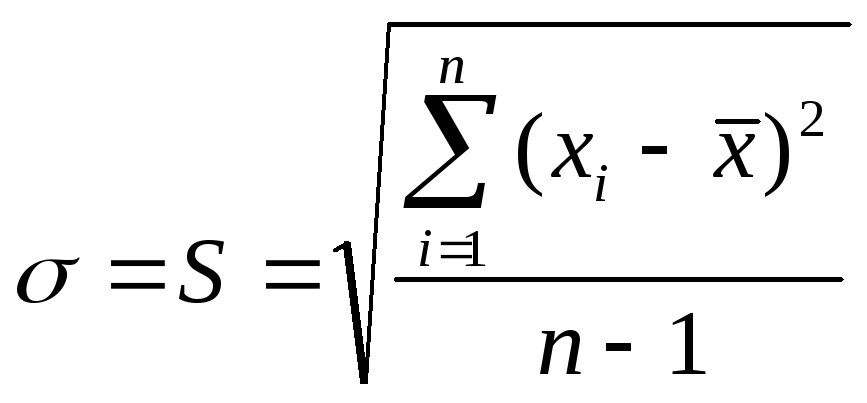
Погрешность среднего арифметического значения или оценка среднеквадратического отклонения результата измерений:
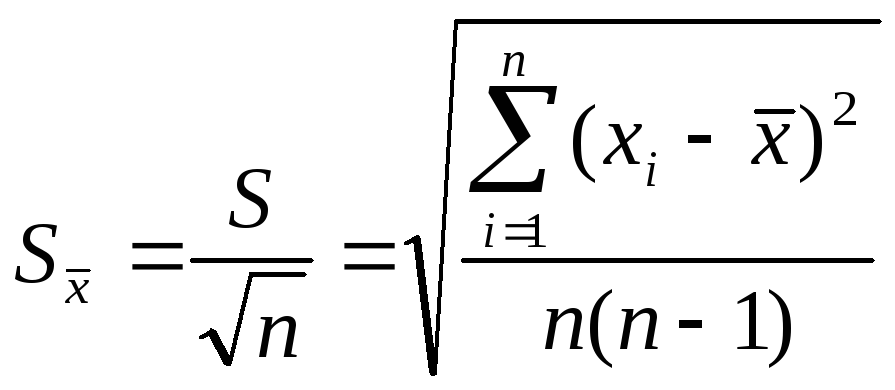
![]() -
точечные оценки случайной погрешности
-
точечные оценки случайной погрешности
Результат измерений
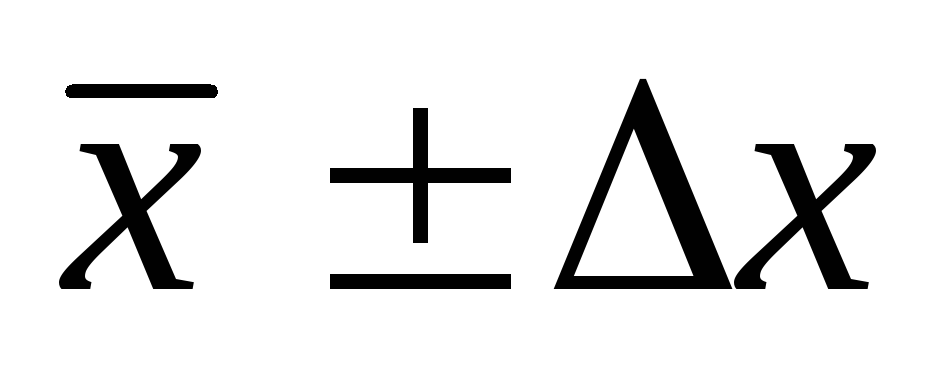
![]() -
среднее квадратическое отклонение
-
среднее квадратическое отклонение
![]() результата
измерения
результата
измерения
![]() -
i-ый
результат наблюдения;
-
i-ый
результат наблюдения;
![]() -
среднее арифметическое исправленных
результатов;
-
среднее арифметическое исправленных
результатов;
![]() -
число результатов наблюдений;
-
число результатов наблюдений;
![]() -
оценка среднеквадратического отклонения
результата измерения.
-
оценка среднеквадратического отклонения
результата измерения.
ВЫВОД: чтобы оценить случайную погрешность результатов измерений надо:
Получить как можно больше результатов измерений
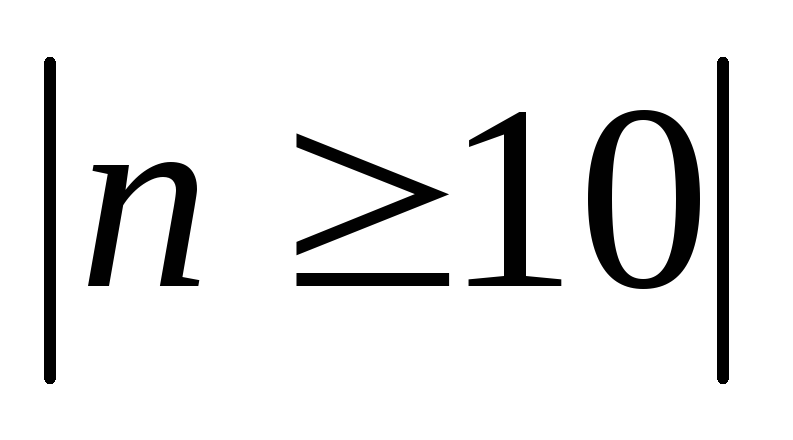 ;
;Рассчитать среднее арифметическое
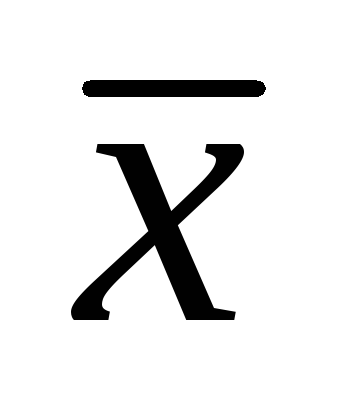 ;
;Рассчитать среднеквадратическое
 (СКО);
(СКО);Рассчитать погрешность среднего арифметического
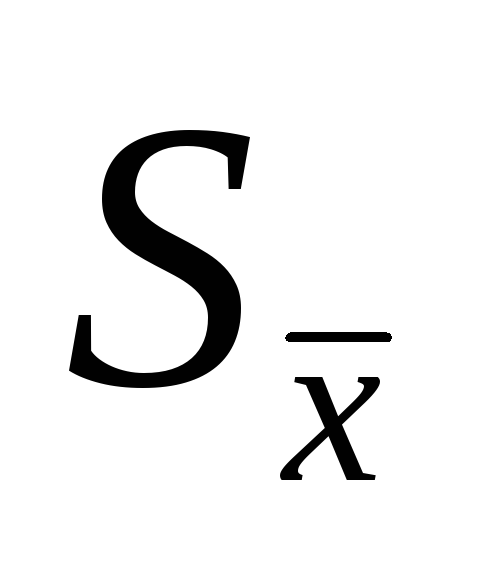 ;
;Вычисляем доверительные границы случайной погрешности:
![]() ,
где t
–коэффициент Стьюдента при P;
n;
,
где t
–коэффициент Стьюдента при P;
n;
Вычисляем доверительные границы неисключенной систематической погрешности результата измерений:
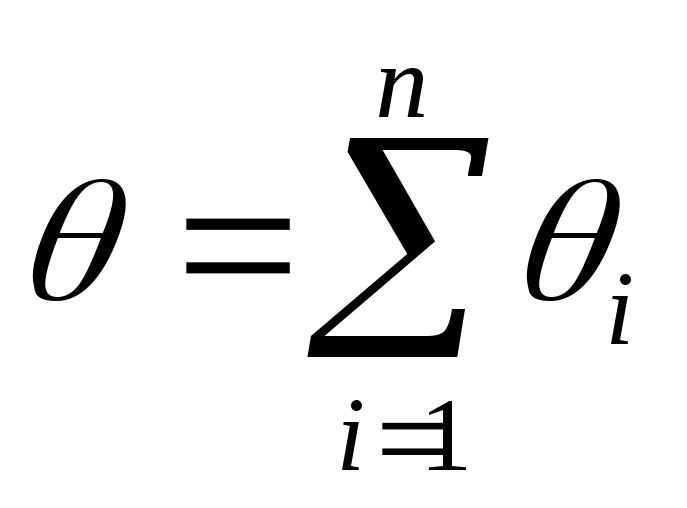 ,
при
,
при
 ;
; ,
при
,
при
 ,
,где N – число погрешностей; к = 1,1 Р = 0,95
Оценка суммарной погрешности:
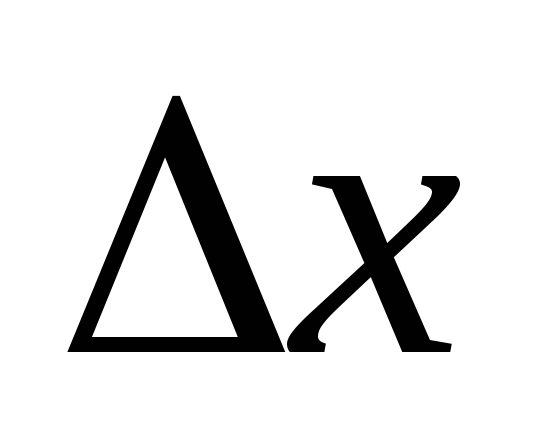
![]() ,
,
если
![]() в 3 и более раз, то
в 3 и более раз, то![]()
если
![]() в 3 и более раз, то
в 3 и более раз, то![]() ,
или:
,
или:
 -
то исключаем систематическую, т.е.
-
то исключаем систематическую, т.е.
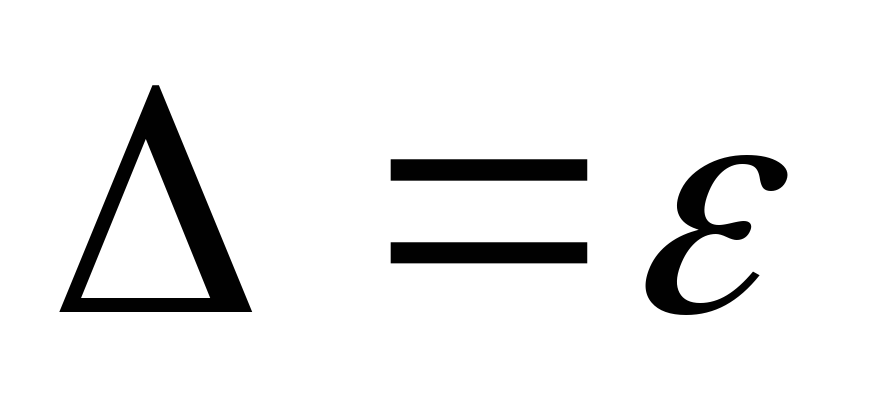
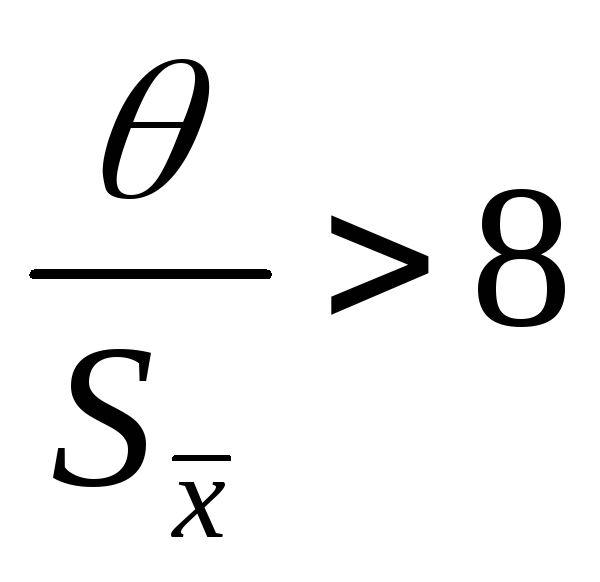 -
то исключаем случайную, т.е.
-
то исключаем случайную, т.е.
 ;
; -
то учитываем обе.
-
то учитываем обе.
ВЫВОД: погрешность любого результата состоит их систематических и случайных погрешностей, чтобы оценить систематические – нужно результат измерения сравнить с эталоном; чтобы оценить случайную – провести многократные измерения.
Обработка результатов прямых измерений
(ГОСТ 8,207-76) Прямые измерения с многократными наблюдениями
Методы обработки результатов наблюдения, т.е. найти истинное значение результата и погрешность: или когда нужно оценить погрешность прибора.
Порядок обработки:
(Имеем
ряд результатов:
![]() )
)
Исключаем известные систематические погрешности из результатов наблюдений (лучше поправками).
Проверяем результаты наблюдений на наличие грубых выбросов, промахов:
Располагаем результаты по возрастанию с min по max:
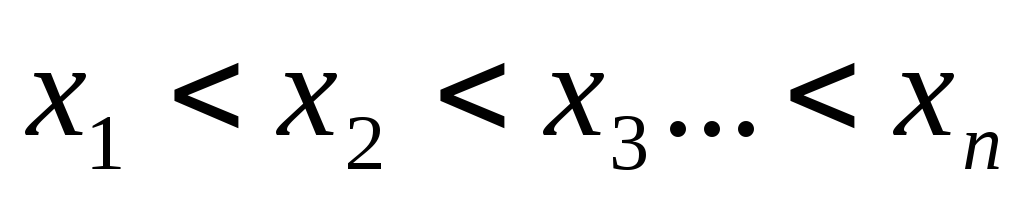 ;
;Находим среднее арифметическое значение:
 ;
;Находим среднеквадратическое отклонение:
 ;
;Находим соотношение для проверяемого результата
 :
:
![]() ,
если
,
если
![]() ,
то результат является анормальным и
подлежит исключению.
,
то результат является анормальным и
подлежит исключению.
Вычисляем СКО:
 ;
;Вычисляем погрешность среднего арифметического результата измерений:
 .
.
Вычисляем доверительные границы случайно составляющей погрешности измерения – определяем коэффициент Стьюдента t при P:
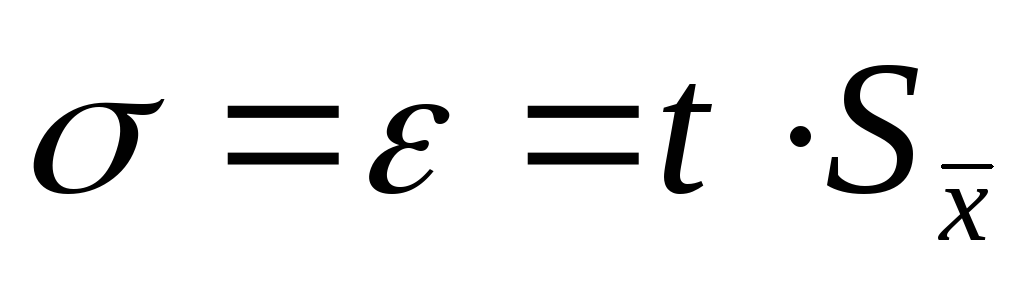 ,
,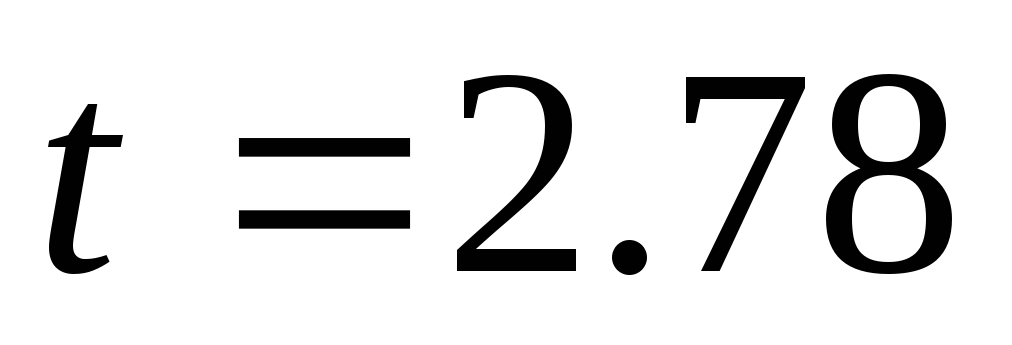 ,
, ,
, .
.Вычисляем доверительные границы не исключенной систематической погрешности результата измерений:
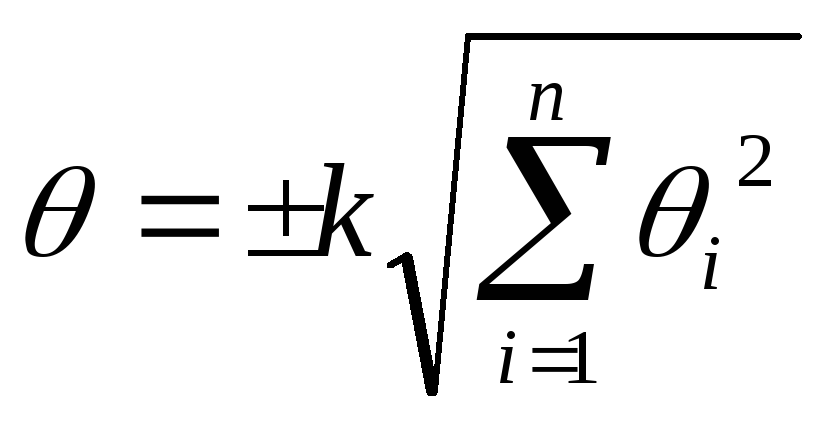 ;
; при
при
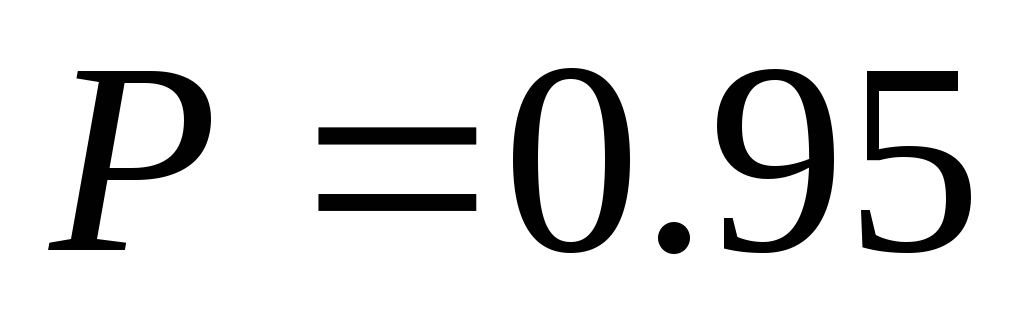 .
.Оценка суммарной погрешности результата измерений, т.е. границ погрешности. Чтобы оценить полную, нужно найти соотношение между случайной и систематической погрешностями:
Если
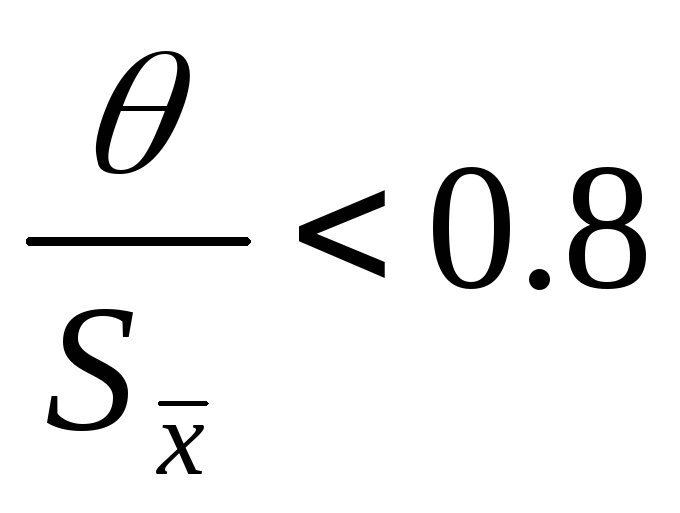 ,
то исключаем систематическую;
,
то исключаем систематическую;Если
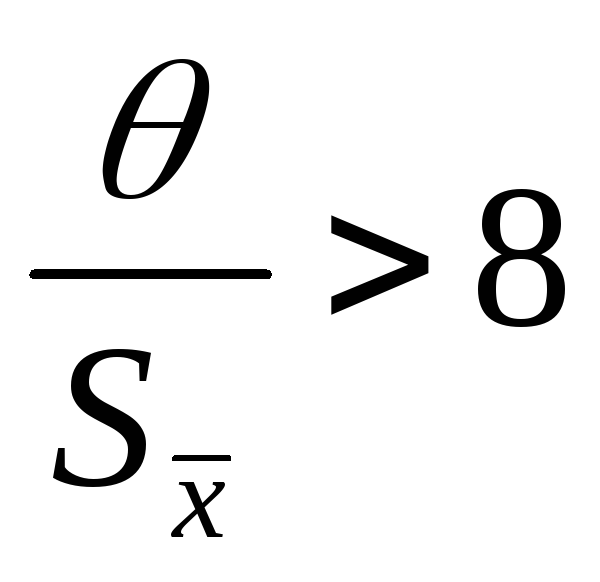 ,
то исключаем случайную;
,
то исключаем случайную;Если
 то учитываем обе.
то учитываем обе.
ИЛИ:
Вычисляем абсолютную погрешность
измерения
![]() .
Если случайная погрешность
.
Если случайная погрешность![]() сравнима с систематической
сравнима с систематической![]() ,
то ошибка измерения
,
то ошибка измерения![]() :
:![]() ,
,
если
![]() ,
то
,
то![]() ;
;
если
![]() ,
то
,
то![]() .
.
