
Сопромат сборник
.pdfФедеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения
Кафедра «Механика деформированного твердого тела, основания и фундаменты»
В. В. Орлов
Сопротивление материалов с основами строительной механики
Екатеринбург Издательство УрГУПС
2012
Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения
Кафедра «Механика деформированного твердого тела, основания и фундаменты»
В. В. Орлов
Сопротивление материалов с основами строительной механики
Сборник контрольных заданий с методическими указаниями для слушателей профессиональной переподготовки
по программе «Промышленное и гражданское строительство»
Екатеринбург Издательство УрГУПС
2012
УДК 539.3/6 O66
Орлов, В. В.
O66 Сопротивление материалов с основами строительной механики : сб. контр. заданий / В. В. Орлов. – Екатеринбург : Изд-во УрГУПС, 2012. – 14, [2] с.
Представлены контрольные задания для слушателей профессиональной переподготовки по программе «Промышленное и гражданское строительство».
Приведены примеры расчета для каждого задания с необходимыми пояснениями на каждой стадии расчета.
Выполнение заданий позволит закрепить теоретические знания и получить практические навыки расчета.
УДК 539.3/.6
Печатается по решению редакционно-издательского совета университета
Автор: В. В. Орлов – доцент кафедры «Механика деформируемого твёрдого тела, основания и фундаменты», УрГУПС
Рецензент: Н. Г. Горелов – доцент кафедры «Строительные конструкции и строительное производство», канд.техн. наук, УрГУПС
©Уральский государственный университет путей сообщения (УрГУПС), 2012
ОГЛАВЛЕНИЕ |
|
Задание № 1................................................................................................................................... |
4 |
Пример расчета статистически определяемой балки ................................................................... |
6 |
Задание № 2..................................................................................................................................... |
9 |
Пример расчета статистически определимой рамы .................................................................... |
10 |
3
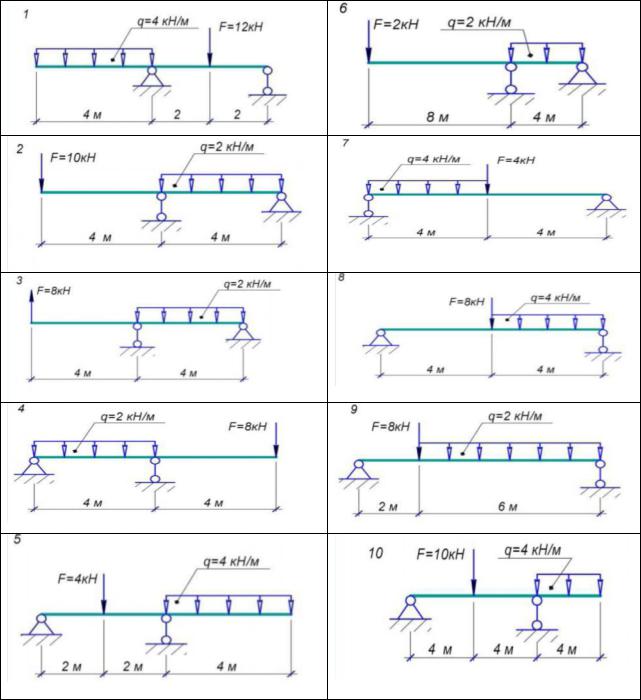
ЗАДАНИЕ № 1
Для заданной статически определяемой балки требуется:
1.Определить опорные реакции.
2.Вычислить значения поперечных сил в характерных точках и построить эпюру поперечных сил (Эп. «Q»).
3.Вычислить значения изгибающих моментов в характерных точках и построить эпюру изгибающих моментов (Эп. «М»).
4.Их условия прочности при изгибе по нормальным напряжениям подобрать сечение балки в виде двутавра, если R = 20 кН/см2.
4
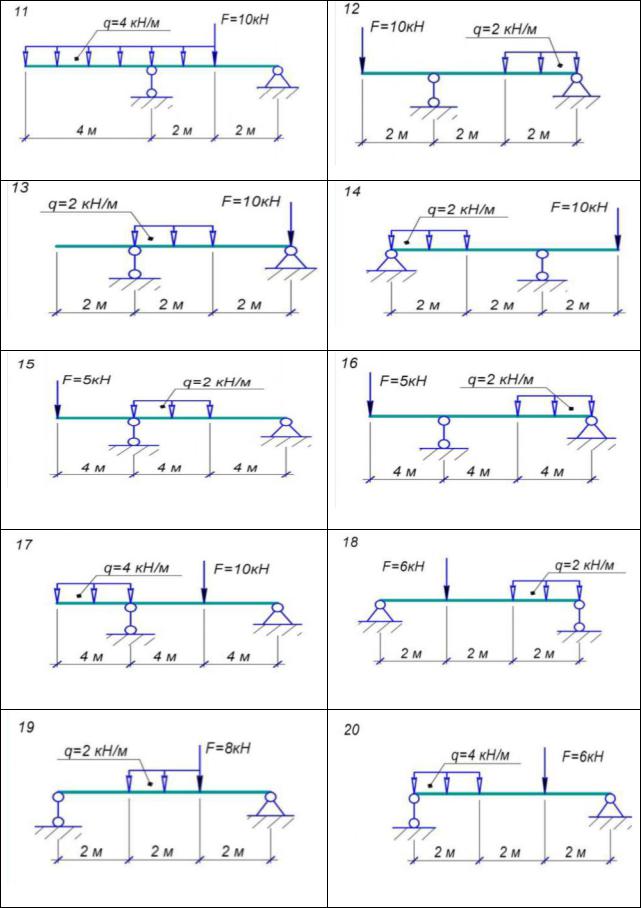
5
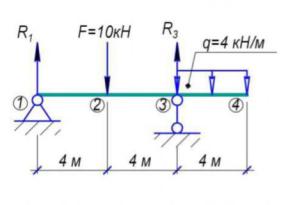
ПРИМЕР РАСЧЕТА СТАТИЧЕСКИ ОПРЕДЕЛЯЕМОЙ БАЛКИ
1.Определим в балке характерные точки.
Точки 1, 2, 3, 4 – характерные.
2.Определим опорные реакции (R1 и R2).
Для определения опорной реакции R1
составим уравнение моментов всех сил относительно точки «3».
R1` ´8 - F ´4 + q ´ 4´ 2 = 0
R = |
F ´ 4 - q ´8 |
= |
10 ´ 4 - 4 ´8 |
= 1 kH |
|
|
|||
1 |
8 |
8 |
|
|
|
|
|||
Для определения опорной реакции R3 составим уравнение моментов всех сил относительно точки «1».
- R3 ´ 8 + F ´ 4 + q ´ 4 ´ (8 + 2) = 0
R = |
F ´ 4 + q ´ 4 ´10 |
= |
40 +160 |
= 25 kH |
|
|
|||
3 |
8 |
8 |
|
|
|
|
|||
Проверка правильности определения опорных реакций: составим уравнение
–сумма проекций всех сил на ось Y.
åFy = 0 R1 + R2 - F - q ´ 4 = 0
1 + 25 -10 - 4 ´ 4 = 16 -16 = 0
Опорные реакции найдены верно.
3. Определение значений поперечных сил в характерных точках.
|
Q лев = 0; |
Q пр = R = 1 |
kH |
||
|
1 |
|
1 |
1 |
|
Q лев = R = 1 |
kH ; |
Qпр |
= R - F = 1 -10 = -9 kH |
||
2 |
1 |
|
2 |
2 |
|
|
Q лев |
= R - F = 1 -10 = -9 |
kH ; |
||
|
3 |
1 |
|
|
|
Q3пр = R1 - F + R2 = 1 -10 + 25 = 16 kH
Q4 = 0
6
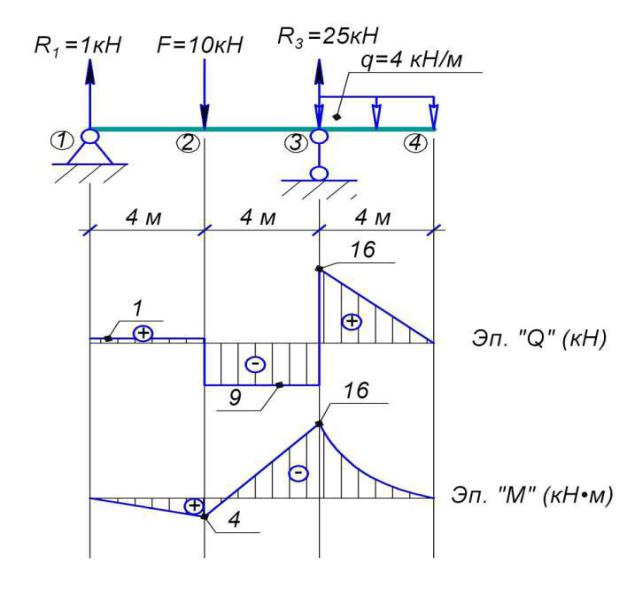
4. Определение значений изгибающих моментов в характерных точках.
M1 = 0
M 2 = R1 ´ 4 = 1´ 4 = 4 kH ´ м
M 3 = R1 ´8 - F ´ 4 = 1´8 -10 ´ 4 = -32 kH ´ м
M 4 = 0
5. Строим эпюры поперечных сил и изгибающих моментов в балке.
7
|
|
|
6. Подбор сечения балки в виде твутавра. |
||||||||||||||||
|
|
|
|
|
|
|
|
σ |
max |
= |
|
|
M max |
|
|
£ R |
– условие прочности при изгибе |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Wx |
|
|
|
|
n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где: σ – нормальное напряжение; |
|||||||||||||||||||
Rn |
= 20kH / см2 |
– расчетное сопротивление; |
|||||||||||||||||
M max = 16kH × м = 16 ´102 kH × см – берется с эпюры « М »; |
|||||||||||||||||||
Wx |
– момент сопротивления при изгибе – геометрическая характеристика сечения. |
||||||||||||||||||
Wx |
³ |
|
M max |
|
= |
16 ´102 |
= |
80 см |
2 |
. |
|
|
|||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
Rn |
|
|
|
20 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из сортамента по ГОСТ 8239-89 выбираем двутавр № 14 Wx = 81 см3 .
8
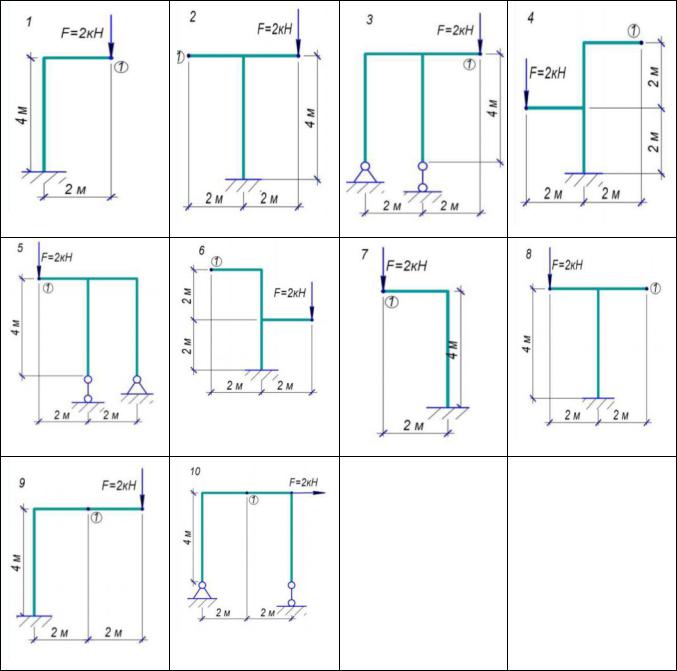
ЗАДАНИЕ № 2
Для заданной статически определяемой рамы требуется:
1.Определить опорные реакции.
2.Построить эпюры изгибающих моментов, поперечных сил и продольных усилий.
3.Определить вертикальный прогиб заданной точки (т. 1), если жесткости всех стержней постоянны (EJ – const).
9
