
Крат. и криволин. интегр
..pdf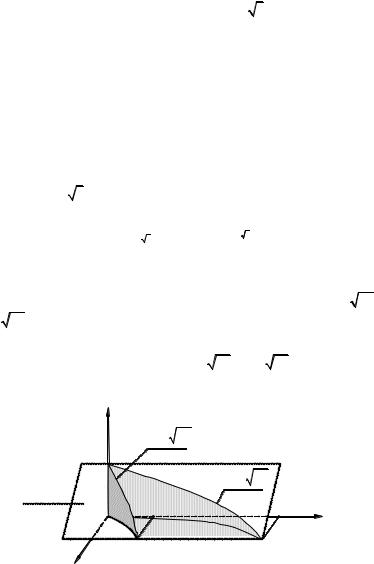
x2 |
+ |
y2 |
=1 →ρ2 =1 →ρ =1, |
||||||
4 |
|
|
|
||||||
|
|
|
16 |
|
|
|
|||
x2 |
|
|
+ |
y2 |
|
=1 →ρ2 =5 →ρ = 5 . |
|||
4 5 |
|
|
|||||||
|
16 |
5 |
|||||||
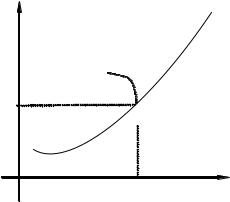
Из рисунка видно, что интервал изменения угла поворота луча
на заштрихованной области составляет |
π |
радиан. |
||||||||||
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, границы области D в полярной системе коорди- |
||||||||||||
нат определяются системой неравенств |
|
|
|
|
|
|
||||||
|
π |
≤ ϕ≤ |
π |
, |
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
||
|
|
Тогда площадь фигуры равна |
||||||||||
|
|
|
||||||||||
D : |
|
|
|
|||||||||
|
1 ≤ρ≤ |
5 . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
π |
|
|
|
|
5 |
π |
|
|
|
|
2 |
5 |
2 |
|
ρ2 |
|
2 |
||
|
|
|
|
|
||||||||
∫∫a bρdρdϕ = ∫2 4dϕ∫ρdρ =8∫dϕ |
2 |
|
|
=16∫dϕ = 4π. |
||||||||
|
D |
|
|
π |
1 |
π |
|
|
1 |
π |
||
|
|
|
|
4 |
|
4 |
|
|
|
|
|
4 |
4. Найти объем тела V, ограниченного поверхностями: y = 3x, y =3 3x, x + z = 3, z = 0.
Решение. Построим пространственную область V, ограниченную
цилиндрическими поверхностями: y = |
3x, y =3 3x и двумя плос- |
|
костями: x + z = 3, z = 0, (рис. 12). |
|
|
z |
|
|
|
y = 3 x |
|
3 |
|
|
|
|
y =3 3x |
z =3 −x |
3 |
9 |
0 |
||
3 |
|
y |
x
Рис. 12
21
Границы выделенной области определяются системой
|
0 ≤ x ≤3, |
|
|
|
||
|
3x ≤ y ≤3 3x, |
|
|
|||
V : |
|
|
||||
|
0 ≤ z ≤3 − x . |
|
|
|||
|
|
|
||||
|
|
|
|
|
||
Тогда объем тела равен |
|
|
|
|
|
|
V = ∫∫∫dxdydz = ∫3 dx3 ∫3x dy3∫−x dz = |
72 |
. |
||||
5 |
||||||
V |
0 |
3x |
0 |
|
||
|
|
|||||
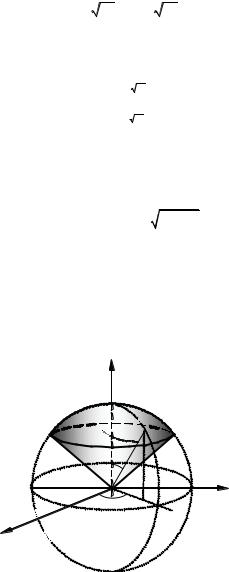
5.Найти объем тела V, ограниченного поверхностями: x 2 + y 2 + z 2 = = R 2, z2 = x 2 + y 2, (z ≥ 0).
Решение. Преобразуем второе уравнение:
z2 = x2 + y2 → z = ± x2 + y2 .
Это уравнение определяет поверхность конуса, образующие ко-
торой образуют осью Oz угол θ = π радиан.
4
Уравнение x 2 + y 2 + z 2 = R 2 определяет сферическую поверхность с центром в точке O(0; 0) и радиусом R . Построим пространственную область V (рис. 13) и перейдем в сферическую систему координат.
z
 R
R
ρ


 •
•



 θ
θ
0 
φ |
y |

 R x
R x 


Рис. 13
22
Используем соотношения: x = ρ sinθ cosφ, y = ρsinθsinφ, z = ρcosθ. Из рисунка можно определить систему неравенств, описывающих об-
|
0 |
≤ ϕ≤ 2π, |
||
|
|
|
π |
|
|
0 |
≤ θ≤ |
, |
|
ласть интегрирования V : |
4 |
|||
|
|
|
|
|
0 ≤ρ≤ R .
Составим тройной интеграл и вычислим объем тела
ππ
V = ∫∫∫ρ2 sin θdρdϕdθ = |
2∫πdϕ∫4 sin θdθ∫R ρ2dρ = |
2πR3 |
∫4 sin θdθ = |
2 − 2 |
πR3 . |
||
3 |
3 |
||||||
V |
0 0 |
0 |
0 |
|
|||
|
|
|
|||||
6. Найти массу плоской неоднородной пластинки, ограниченной линиями: y = x 2, x = 0, y = 1. Поверхностная плотность в каждой точке фигуры равна удвоенному расстоянию от оси Оy.
Решение
Построим чертеж фигуры D (рис. 14).
y 
1
2x
•
0 |
1 |
x |
Рис. 14
Границы заштрихованной области
0 ≤ x ≤1,
D :
2 ≤ ≤x y 1.
23
Из условия получим функциональное выражение для плотности γ = 2x.
Составим двойной интеграл и вычислим массу плоской пластинки
m = ∫∫γdxdy = 2∫1 dx ∫1 |
xdy = 2∫1 x(1 − x 2 )dx = |
1 |
. |
||
2 |
|||||
D |
0 x 2 |
0 |
|
||
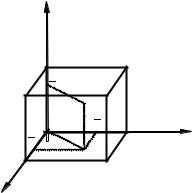
7. Найти массу, координаты центра тяжести неоднородного куба, моменты инерции относительно оси Ox и координатной плоскости xOy. Грани куба заданы координатными плоскостями и плоскостями x = 1, y = 1, z = 1. Объемная плотность куба в каждой точке равна произведению ее координат γ(x; y; z) = xyz.
Решение. Сделаем чертеж тела V (рис. 15), оно представляет собой куб, расположенный в первом октанте с ребром, длина которого равна единице.
z
1
|
2 |
С |
|
|
3 |
|
|
|
|
● |
|
|
0 |
2 |
1 |
2 |
3 |
||
|
|
y |
|
3 |
|
|
1
x
Рис. 15
Из рисунка видно, что все пределы интегрирования – постоянные. Найдем массу тела
|
1 |
1 |
1 |
1 |
|
|
m = ∫∫∫ γ(x; y;z )dxdydz = ∫dx ∫dy ∫ xyzdz = |
. |
|||||
8 |
||||||
V |
0 |
0 |
0 |
|
||
|
|
|||||
Определим координаты центра тяжести
|
1 |
|
1 |
1 |
1 |
2 |
|
|
xc = |
∫∫∫ γxdxdydz =8 ∫dx ∫dy ∫ x 2 yzdz = |
, |
||||||
m |
3 |
|||||||
|
V |
0 |
0 |
0 |
|
|||
|
|
|
|
|||||
24

|
|
|
1 |
|
|
|
1 |
|
1 |
1 |
|
|
2 |
|
||||
yc |
= |
|
∫∫∫ γydxdydz =8 ∫dx ∫dy ∫ xy 2 zdz = |
, |
||||||||||||||
m |
3 |
|||||||||||||||||
|
|
|
|
V |
|
0 |
0 |
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
m ∫∫∫ |
|
1 |
|
1 |
|
1 |
|
3 |
|
|
||||
|
|
|
|
|
∫ |
|
∫ |
|
∫ |
|
|
|
||||||
z |
|
= |
1 |
|
|
γzdxdydz =8 |
|
dx |
|
dy |
|
xyz 2dz = |
2 |
. |
||||
c |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
V |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
Момент инерции относительно оси Ox находим по формуле
1 1 1
J x = ∫∫∫( y 2 +z 2 )γdxdydz = ∫dx ∫dy ∫( y 2 +z 2 )xyzdz =
V |
|
0 0 0 |
|
|
|
1 |
1 |
1 |
1 |
|
|
= ∫ xdx ∫ ydy ∫( y 2 +z 2 )zdz = |
. |
||||
8 |
|||||
0 |
0 |
0 |
|
||
|
|
||||
Момент инерции относительно плоскости xOy находим по формуле
J xy = ∫∫∫z 2 γdxdydz = ∫1 dx ∫1 dy ∫1 xyz 3dz = ∫1 xdx ∫1 |
ydy ∫1 z 3dz = |
1 |
. |
||||||
|
|||||||||
V |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
|
|
|
|
|
|||||||
Задания для самостоятельной работы
1. Найти площадь плоской фигуры D, ограниченной линиями
y = 2x – x 2, y = x 2. |
(Ответ: |
|
1 |
|
.) |
|||||||
|
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Найти площадь области, ограниченной линиями: |
x2 |
+ |
y2 |
=1 , |
||||||||
|
|
|||||||||||
|
|
|
|
|
4 |
1 |
π |
|||||
|
|
1 |
|
|
|
|
|
|
|
|||
y ≤ |
x, y ≥ 0 |
(Ответ: |
|
|
.) |
|||||||
|
|
4 |
||||||||||
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|||
3. Найти объем тела V, ограниченного поверхностями: |
|
|
|
|
|
|
||||||
|
y2 |
|
|
|
|
|
|
|
|
|||
z = |
|
|
|
, 2x +3y =12 , x = 0 , y = 0 , z = 0 . |
(Ответ: 16.) |
|||||||
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
4. Найти массу однородной плоской пластинки, ограниченной
линиями: y = x 2, y = x . |
(Ответ: |
1 |
.) |
|
3
5. Найти координаты центра масс однородного тела, ограниченного координатными плоскостями и плоскостью x + y + z = 6.
(Ответ: C 3; 3; 3 .)2 2 2
25
ГЛАВА 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
2.1. Криволинейный интеграл 1-го рода
Определение
Пусть вдоль гладкой кривой L расположены массы с известной линейной плотностью (рис. 16). Определим массу m кривой L. Меж-
ду концами А и В кривой вставим произвольно ряд точек А = А0, А1,...
Аn–1, An = B. Возьмем какую-нибудь точку M [Ai, Ai+1], плотность
в этой точке γ(Mi). Приближенно считая, что плотность на участке
[Ai, Ai+1] равна γ(Mi) и обозначая длину дуги Ai, Ai+1 через li, для мас- |
|||
сы этой дуги получаем mi γ(Mi) li . |
|
|
|
y |
|
В● |
|
|
|
||
|
|
• |
ln |
|
γ (Mi ) |
• … |
|
ηi |
Mi |
• … |
|
● |
|
||
|
• |
li |
|
А |
• … |
|
|
● |
• l2 |
|
|
0 |
l1 |
ξi |
|
|
x |
||
Рис. 16
|
n |
Для массы всей кривой имеем m ∑γ(Mi ) li . Устремляя к нулю |
|
|
i =1 |
наибольшую из длин li , получаем точное равенство |
|
|
n |
m = liml →0 |
∑γ(Mi ) li . |
i |
i =1 |
|
|
Рассмотрим предел такого рода для произвольной функции f(M) = f(x; y), определенной на кривой L. Разобъем эту кривую L
26
на элементарные дуги, выберем на каждой из них некоторую точку
n |
|
Мi и составим интегральную сумму: I ( Ai ;Mi ) = ∑ f (ξi ;ηi ) |
li . |
i =1 |
|
Число I называется пределом интегральных сумм при |
l → 0, если |
ε > 0, δ > 0 и такое, что для любого разбиения кривой L, у которо- |
|
го l < δ, и для любого выбора промежуточных точек М выполняет-
ся неравенство WI(Ai; Mi) – I W < ε.
Если существует предел lim I ( Ai ;Mi ) = I , то число I называется
l →0
криволинейным интегралом первого рода от функции f(x; y) по кривой L и обозначается ∫ f (x; y)dl .
L
Если кривая L незамкнутая и точки А и В ее концы, то криволинейный интеграл первого рода обозначается следующим образом:
∫ f (x; y)dl .
AB
Из определения следует, что криволинейный интеграл первого рода не зависит от того, в каком направлении (от А до В или от В до А) пробегается кривая L:
∫ f (x; y)dl = ∫ f (x; y)dl.
AB BA
Криволинейные интегралы 1-го рода обладают всеми свойствами, аналогичными свойствам определенного интеграла: линейность, аддитивность, модуль интеграла не превосходит интеграла от модуля функции. Справедлива также формула среднего значения.
Вычисление криволинейного интеграла первого рода
Во многих случаях вычисление криволинейного интеграла 1-го рода сводится к нахождению некоторого обыкновенного определенного интеграла.
Если кривая L задана параметрическими уравнениями x = x(t) и y = y(t), где p ≤t ≤q, тогда длина dl элементарной дуги кривой равна
dl = (xt ')2 +( yt ')2 dt,
а криволинейный интеграл выражается обыкновенным определенным интегралом по следующей формуле:
q
∫ f (x; y)dl = ∫ f (x(t); y(t)) (xt ')2 +( yt ')2 dt.
L p
27
Если кривая L имеет явное задание y = y(x), где a ≤x ≤b, тогда криволинейный интеграл вычисляется по следующей формуле:
∫ f (x; y)dl = ∫b |
f (x; y(x)) 1 +( yx ')2 dx. |
|
L |
a |
|
Если кривая задана уравнением в полярных координатах ρ = ρ(φ), где α ≤ φ ≤ β, тогда криволинейный интеграл вычисляется по следующей формуле:
β
∫ f (x; y)dl = ∫ f (ρ;ρ(ϕ)) ρ2 +(ρϕ ')2 dϕ.
Lα
Для случая пространственной кривой L при параметрическом задании кривой уравнениями x = x(t), y = y(t), z = z(t) где p ≤ t ≤ q, длина dl элементарной дуги кривой равна
dl = (xt ')2 +( yt ')2 +(zt ')2 ,
а криволинейный интеграл выражается обыкновенным определенным интегралом по следующей формуле:
q
∫ f (x; y; z)dl = ∫ f (x(t); y(t); z(t)) (xt ')2 +( yt ')2 +(zt ')2 dt.
L p
Примеры
1. Вычислить криволинейный интеграл 1-го рода ∫ |
y |
dl , где L – уча- |
|||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
x |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|||
сток параболы y = |
|
|
x |
|
, лежащий между точками A 1; |
|
и B (2; 2). |
||||||||||
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
Решение. Найдем dl = |
1 +( yx′)2 dx = |
1 + x2 dx . Тогда наш интеграл |
|||||||||||||||
будет равен ∫ |
y |
dl = |
1 |
∫2 x |
1 + x2 dx = |
1 |
( |
125 − 8) . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
L |
x |
2 |
1 |
|
6 |
|
|
|
|
|
|
||||||
2. Вычислить криволинейный интеграл 1-го рода ∫ |
x2 + y2 dl , где |
||||||||||||||||
L – окружность x 2 + y 2 = ax(a > 0). |
|
|
L |
|
|
||||||||||||
Решение. Введем полярные координаты x = ρcosφ, y = ρsinφ. Тогда уравнение окружности примет вид x2 +y2 =ax →ρ2 =aρcosφ →ρ = acosφ, а элемент дуги dl = ρ2 +ρ′ϕ2 dϕ= a2 cos2 ϕ+a2 sin2 ϕdϕ= adϕ.
28
|
|
|
|
|
|
|
a |
|
|
|
|
Так как центр окружности имеет координаты C |
|
;0 |
|
, а радиус |
|||||||
|
|||||||||||
|
a |
|
π |
|
π |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
R = |
|
, то ϕ − |
2 |
; |
2 |
. |
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
Следовательно,
ππ
|
2 |
2 |
∫ |
x 2 + y 2 dl = ∫ ρ adϕ =a2 |
∫ cos ϕdϕ = 2a2 . |
L |
−π |
−π |
|
2 |
2 |
3. Вычислить криволинейный интеграл 1-го рода ∫ye−x dl , где L –
L
дуга линии x = ln(1 + t 2), y = 2arctgt – t, описываемая при изменении t от 0 до 1.
Решение. Будем использовать формулу для кривой, заданной па-
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
раметрически: ∫ f (x; y)dl = ∫ f (x(t ); y(t )) |
(xt′)2 +( yt′)2 dt . |
||||||||||||||||
L |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||
Найдем: xt′ = |
|
2t |
, |
y′ = |
1 −t 2 |
, |
e |
−x |
= e |
−ln(1+t2 ) |
= |
|
1 |
|
. |
||
|
+t 2 |
|
|
|
|
|
|
|
|||||||||
|
1 +t 2 |
|
|
|
|
+t 2 |
|||||||||||
1 |
|
t |
|
|
|
|
|
|
1 |
|
|||||||
Получим dl = |
(xt′)2 +( yt′)2 dt = dt , тогда наш интеграл будет равен |
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
dt |
= π |
2 |
|
ln 2 |
|
|
||
∫ ye x dl = ∫(2arctgt −t ) |
− |
. |
|||||||||||||||
2 |
|
||||||||||||||||
L |
|
|
0 |
|
|
|
|
1 +t |
16 |
|
2 |
|
|
||||
Задачи для самостоятельной работы
1. Вычислить криволинейный интеграл 1-го рода ∫(4 3 x −3 y )dl :
|
L |
|
|
|
a) на отрезке между точками A(–1; 0) и В (0; 1). |
(Ответ: −5 |
2.) |
||
|
46 |
|
||
б) по дуге астроиды x = cos3t, y = sin3t. |
(Ответ: – |
|
|
.) |
|
7 |
|||
|
|
|
|
|
2. Вычислить криволинейный интеграл 1-го рода ∫(x − y)dl меж-
|
L |
5 |
|
|
ду точками A(0; 0) и B(4; 3). |
(Ответ: |
.). |
||
|
||||
2 |
||||
|
|
|
29
2.2. Криволинейный интеграл 2-го рода
Определение
Пусть функция f(x; y) определена на кривой L, имеющей концы А и В. В отличие от криволинейных интегралов 1-го рода кривая АВ рассматривается как направленная линия (рис. 17).
y |
|
|
В |
|
Q(Mi ) |
|
● |
|
• |
ln |
|
|
|
||
|
P (Mi) |
… |
|
|
• |
|
|
yi |
|
• … |
|
Mi |
● |
|
|
|
• |
li |
|
А |
• … |
|
|
● |
• l2 |
|
|
|
l1 |
|
|
0 |
|
х i |
x |
|
Рис. 17 |
|
|
Пусть А – начало, а В – конец этой кривой. Разобьем кривую L
точками A = A0, A1,...An–1, An = B в направлении от А к В. На каждой дуге AkAk–1 выберем по точке (xk; yk) и составим сумму:
n
∑ f (xk ; yk )(xk − xk −1 ).
k =1
Предел этой суммы при стремлении к нулю наибольшей из дуг AkAk–1 называется криволинейным интегралом второго рода по координате x и обозначается через ∫ f (x; y)dy .
AB
Здесь в отличие от криволинейного интеграла 1-го рода важен по-
рядок букв А и В, поскольку ∫ |
f (x; y)dx = − ∫ f (x; y)dx , т. е. при пе- |
AB |
BA |
ремене направления линии, криволинейный интеграл второго рода меняет знак.
30
