Vse_lektsii_TPR_MARK

С математической точки зрения равносилен выбору во множестве векторов и все определения и результаты можно формулировать как в терминах решений, так и в терминах векторов.

Задачу выбора, которая включает множество допустимых решений X и

векторный критерий f , обычно называют многокритериальной задачей или задачей многокритериальной оптимизации.

Отношения предпочтения

Рассмотрим две допустимых альтернативы x1и x2. Допустим, что ЛПР выбирает первое решение. В этом случае пишут

x1 >X x2

Знак >X выражает отношение предпочтения.

Теперь можно сформулировать все основные компоненты задачи много-

критериального выбора.

Постановка всякой задачи многокритериального выбора включает

1)множество возможных решений X ,

2)векторный критерий f вида ,

3) отношение предпочтения >X.

Бинарные отношения

Для описания отношения предпочтения, которым ЛПР руководствуется в процессе выбора, используется понятие бинарного отношения.

Множество Парето

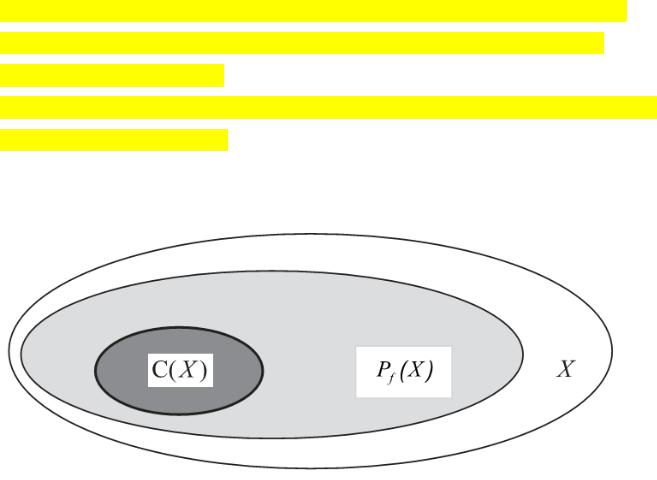
Множество Парето имеет большое значение для решения многокритериальных задач.

Множество Парето образуют все парето-оптимальные решения Парето-оптимальное решение – это такое допустимое решение, которое не может быть улучшено (увеличено) ни по одному из имеющихся критериев без ухудшения ( уменьшения ) по какому-то хотя бы одному другому критерию .

Иначе говоря, предпочитая одному парето-оптимальному решению другое парето-оптимальное решение, ЛПР вынуждено идти на определенный компромисс, соглашаясь на некоторую потерю хотя бы по одному критерию

(получая, разумеется, определенный выигрыш, по крайней мере, по какому-то

другому критерию). По этой причине множество Парето нередко называют

множеством компромиссов.

Если ЛПР ведет себя «разумно», то выбираемые им решения обязательно должны

быть парето-оптимальными.

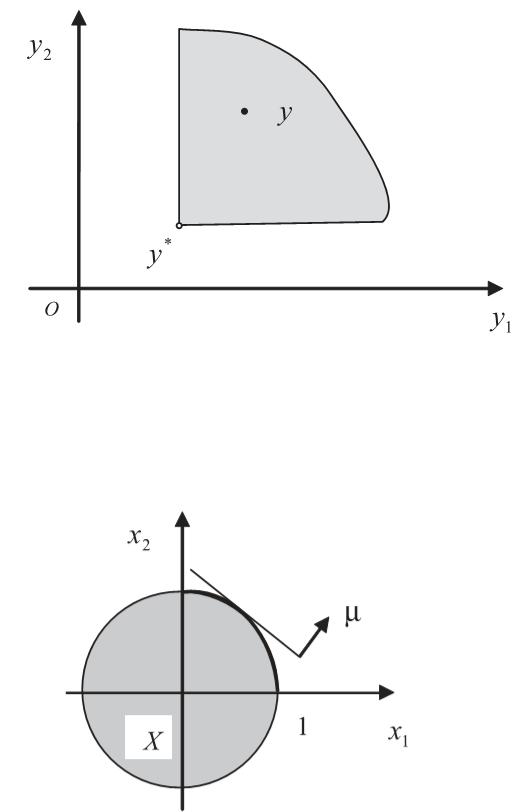
Согласно определению множества Парето вектор y* будет парето-оптимальным,

если для него не существует другого такого вектора y Y , что имеет место неравенство y ≥ y*.

На транспорте возможно принятие решений, которые основаны на многих критериях, при этом для различных решений одни критерии лучше, а другие

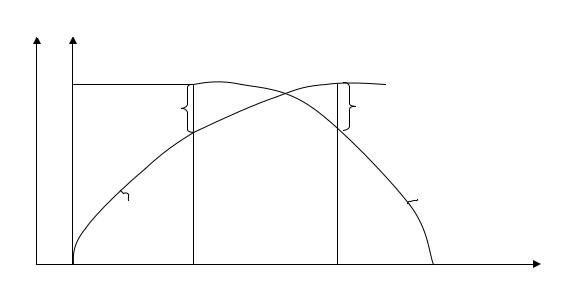
хуже. Если не известно как соотносятся между собой критерии, то грамотное решение принять невозможно. Поэтому необходимо знать хотя бы приблизительно относительную важность критерия.

ПРИМЕР. Имеется сортировочная станция, на которой работают 5 маневровых локомотивов, при этом выходные параметры системы это:

1.Количество расформированных вагонов (составов).

2.Количество сформированных вагонов (составов), переставленных в парк

отправления.

Влияющие на решение средства – это расстановка маневровых локомотивов по маневровым районам.

Имеется 6 вариантов решения.

Изобразим их графически.

4/1 - горочный локомотив / маневровый локомотив y1 – расформирование, y1 = f (x);

y2 - формирование, y2 = f (x).

y1 y2

y1

y2

x2

Принципы выбора решения в условиях многокритериальности

1. Принцип жесткого приоритета

Устанавливаем относительную важность приоритета.

y1 < y3 < y2

Решение в начале оцениваем только по критерию y2, т. е. самому важному, при

этом наибольшему значению критерия y2 может соответствовать несколько

решений. Из решения, которое соответствует max значения y2, выбираем то

значение, которое соответствует максимальному значению y3.

2. Справедливый компромисс

Предполагаем, что все критерии являются приблизительно одинакого важными. Для того, чтобы найти решение соответствующее справедливому компромиссу, вводятся относительные критерии. Например, имеем два параметра y1 и y2 –

характеризующих решения. Причем в области допустимых решений они имеют максимальные значения max y1 и max y2.

Вводим относительные критерии:

y*1 = y1/max y1; y*2 = y2/max y2

Вводится новый глобальный критерий F, который является произведением относительных критериев:

F = y*1 × y*2 → max

3.Скалярная свертка

Вэтом случае необходимо знать количественное соотношение важности критериев. Вводится глобальный критерии F и коэффициенты важности λ частных критериев. Глобальный критерий максимизируется в следующем виде.

λ1 , λ2 – соответственно относительная важность критериев y1 и y2.

9. Подходы к формированию множества возможных альтернатив и способы

сужения множества возможных решений

Существует ли проблема на самом дел?

Вопросы, которые необходимо проверить для определения существования самой

проблемы:

1.Проблема исходной ситуации (граничных условий), необходимо проверить определены ли исходные условия по решаемому вопросу.

2.К кажущимся (иллюзорным) проблемам относятся и такие, решение которых зависит от личных взглядов.

3.Существуют альтернативы (решения), оказывающиеся неправомерными,

поскольку в действительности выбора нет, а существует только жесткая обусловленность.

4. Логические ловушки, т.е. при ближайшем рассмотрении эти задачи открывают противоречия в логике (парадокс Брадобрея).

Проблема формирования исходного множества решений.

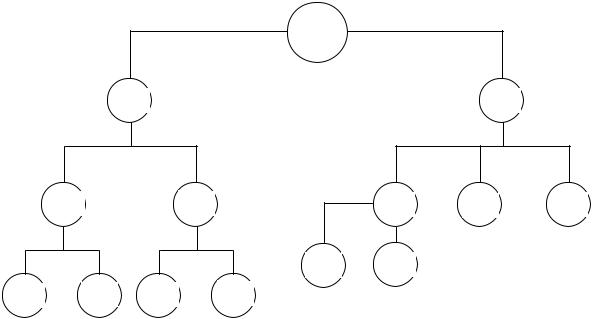
Одним из хороших способов формирования поля решений и проверки этого поля на формульную полноту является метод построения дерева решений.

ПРИМЕР: Проблема Нового года.

Дерево решений проблемы встречи Нового года.

А – проблема встречи Нового Года;

В1 – встречать дома;

В2 – встречать не дома;

С1 – с гостями;

С2 – один;

С3 – с родственниками;

С4 – обратиться в бюро путешествий;

С5 – ресторан или другое место увеселений;

Д1 –за ужином;

Д2 – за дружеской беседой;

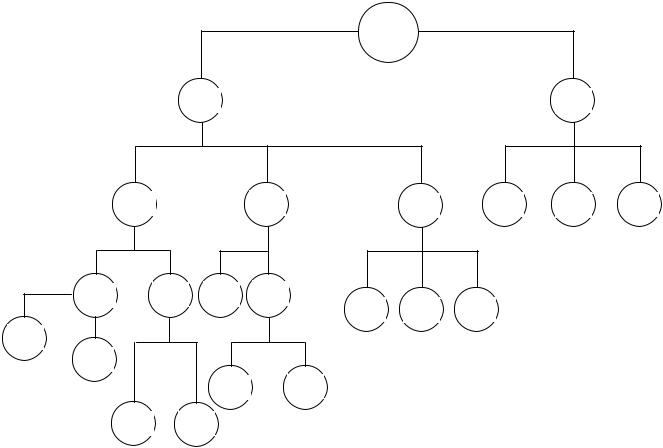
Д7 – использование накопленного тепла;

Е1 – покрытие пленкой в один слой;

Е2 – в 2 слоя;

Е3 – обрызгивание вагона щелочью;

Е4 – обрызгивание вагона маслом;

Е5 – водные растворы;

Е6 – поверхностно-активные вещества.

А

Е3

Е4

Е1 Е2

Укрупненная схема выделения уровней решения проблемы

А – цель решения, главная проблема;

В – стратегия решения;

С – группы методов;

Д – собственно методы;

Е – варианты решения.

При таком подходе единичные варианты на каждом иерархическом уровне в зависимости от решаемой проблемы можно изучать, исследовать и обобщать с помощью математических, естественнонаучных принципов, методов и структур.

Конференция идей

Эффективным способом расширить поле возможных решений и охватить как можно больше вариантов, служит конференция идей. Во время К. И. вокруг одной проблемы в короткий промежуток времени группируется множество идей. Это происходит от того, что большое количество людей обсуждают одновременно одну и ту же проблему, увлекают друг друга обсуждением этой проблемы. К. И.

отличается от обычного заседания, рабочего обсуждения, деловой дискуссии и т.

п. Отличие состоит в творческой атмосфере, которая создается и обеспечивается определенными правилами:

1. Вопрос об участниках.

К. И. – это не опрос экспертов, здесь присутствие непрофессионалов очень даже желательно, желательно привлечь людей, которые собственно к решению данной проблемы не имеют отношения, но в это же время это должны быть люди способные вдуматься в новую для них проблематику.

При проведении таких конференций, важно устранить отношение подчиненности между ее участниками, это гарантирует независимость предложений от мнения руководителей. Круг участников должен быть не менее 4 и не более 12 человек.

2. Вопрос о помещении.

Не рекомендуется проводить К. И. в служебно-административном помещении на рабочем месте. Комната должна быть приветливой,

изолированной от шума. Круглый стол усиливает ощущение равноправия среди участников.

3. Вопрос о длительности.

Мнения по этому вопросу сильно расходятся. Идеальной можно считать «мозговую атаку» в течение 15 мин. Следует помнить, что через 40

минут может наступить равнодушие к принимаемым решениям.проблемы.

4. Проблема правил поведения.

Всякая критика строго запрещена. Поощрения поддерживаются. Как только кто-то позволит себе дать низкую оценку идеи другого участника,

творческая атмосфера в этом кругу нарушается, генерация идей прекращается, метод не работает.

5. Фиксация идей.

Высказывание идей фиксируется без оглядки на их реализуемость,

оценка и отбор проводятся позднее, после конференции. В ходе конференции собирается все: все мнения, предложения, идеи. Постановка проблемы.

Задачу лучше всего выразить в виде краткого точного вопроса (какие возможности есть для…?, что нужно сделать чтобы…?).

Интересной разновидностью К. И. является моноконференция, т. е. это сознательное обсуждение проблемы с самим собой, важно помнить при этом, что задача состоит в генерации максимального числа решений проблемы, а не в их оценке и анализе.

После конференции идей необходимо провести дискуссию, посвященную оценке предложенных решений.