
РАСЧЕТ ШПРЕНГЕЛЬНЫХ ФЕРМ
.pdfСтроительный факультет |
85 |
M4 = M3к − N3к x4 =30 кН м .
Как и следовало ожидать, эпюры внутренних усилий, построенные по предложенному способу (рис. 1, е), не отличаются от эпюр, построенных традиционным способом.
Нами проверена возможность строить таким же способом эпюры внутренних усилий в колонне при центральном растяжении–сжатии и в изгибаемой балке (результаты этих расчетов здесь не приводятся).
Нам кажется, что этот способ расчета имеет право на существование, ведь в ряде случаев решение получается быстрее и проще. Правда, ошибка в усилиях на одном участке испортит все последующие. В этом случае рекомендуем после расчета очередного участка строить эпюры и проверять выполнение свойств эпюр [1]. Кроме того, этот способ можно запрограммировать на компьютере, а уж он-то в расчетах не ошибается.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Александров, А.В. Основы теории упругости и пластичности / А.В. Александров, В.Д. Потапов. − М. : Высшая школа, 2007. − 400 с.
2.Строительная механика. Статика упругих систем /В.Д. Потапов, А.В. Александров
[и др.]. – М. : Высшая школа, 2007. – 511 с.
УДК 624.04(075.8)
А.А. ЛЮХТА, Е.А. ЕФИМОВА, Н.А. КИРЕЕВА, студенты 3 курса, Научный руководитель:
Б.А. ТУХФАТУЛЛИН, канд. техн. наук, доцент
РАСЧЕТ ШПРЕНГЕЛЬНЫХ ФЕРМ
Для перекрытия больших пролетов зданий, мостов используются шар- нирно-стержневые системы (фермы), элементы которых работают на растяже- ние-сжатие. В ряде случаев расчет ферм на постоянную и подвижную нагрузку представляет собой непростую задачу. В первую очередь к таким системам относятся шпренгельные фермы, в которых для создания дополнительных узлов на грузовом поясе и для уменьшения расчетной длины сжатых раскосов устанавливаются дополнительные стержни – шпренгели. В учебной литературе [1] традиционно излагается прием разделенияисходной фермы на основную ферму и шпренгели. При этом необходимо перераспределять нагрузку в узлы основной фермы, суммировать усилия, полученные при расчете стержней различных категорий, строить две линии влияния для стоек в ферме с двухъярусными шпренгелями. Такое разделение на одного стержня на два является, на наш взгляд, искусственным приемом, ведь в реальной конструкции стержень является единым.
С другой стороны, особенность шпренгеля заключается в том, что усилия в дополнительных стержнях решетки (стойки, раскоса шпренгеля) возни-
86 |
Материалы 57-й научно-технической конференции |
кают только при загружении узла грузового пояса и не зависят от распределения усилий в остальных стержнях фермы. Таким образом, следует предварительно определить усилия в этих стержнях от узловой нагрузки (эта элементарная задача будет решена ниже), а затем убрать мешающий для расчета стержень и приложить взамен найденное в нем усилие. Такой же прием можно использовать для построения линий влияния, особенно для стержней фермы с двухъярусными шпренгелями.
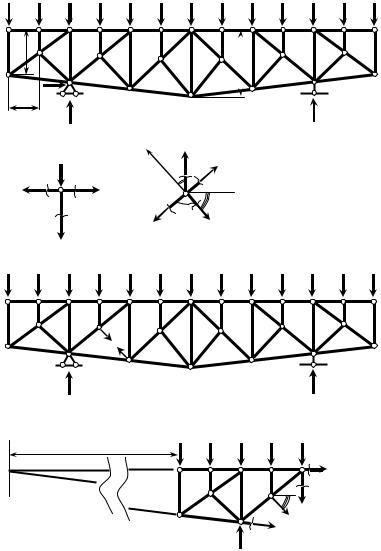
Проиллюстрируем предложенный способ расчета шпренгельной фермы на конкретном примере (рис. 1, а).
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
7 |
|
3 м |
1 |
|
1 |
1 |
|
|
1 |
4,5 м |
1 |
|
|
2 |
|
2 |
|
2 |
|
|
2 |
2 |
|
2 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
8 |
|
|
9 |
|
|
|
|
|
|
|
1 |
1 |
|
HA |
|
|
|
|
|
|
|
|
|
|||
|
2 м |
|
|
1 |
|
1 |
|
1 |
|
|
VB |
|
|
б |
|
|
|
VA |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
y |
|
N16-22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N16-2 |
|
N16-3 |
|
α |
|
|
N22-3 |
cos α = sin β = 0,752 |
||||
|
|
|
|
|
|
|
|
|
sin α = cos β = 0,658 |
||||
|
|
|
|
|
|
|
|
β |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N16-22 |
|
|
N22-9 |
|
90º |
N22-10 |
|
|
|
|
||
в |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F |
F |
F |
F |
F |
F |
F |
F |
F |
F |
F |
F |
F |
2 |
|
|
N22-10 |
|
|
N22-10 |
1 |
VB |
VA |
|
|
|
|
г
F |
F |
F |
F |
F |
24 м |
|
|
|
|
0 |
|
|
|
N3-17 |
|
|
|
|
|
|
|
|
β |
N3-10 |
|
|
|
N22-10 |
|
|
|
VA |
N9-10 |
|
|
|
|
|
|
Рис. 1
|
|
|
Строительный факультет |
|
|
87 |
|||||
Определим продольное усилие в стойке |
N3−10 . |
Предварительно найдем |
|||||||||
усилиев двух стержнях – стойке N16−22 |
и раскосе N22−10 |
(рис. 1, б) поформулам: |
|||||||||
N16−22 |
= −F = −10 кН; N22−10 = N16−22 cosα = −F cosα = −7,52 кН. |
||||||||||
Приложим теперь усилие N22−10 |
к узлам 10 и 22 (рис. 1, в). Рассматривая |
||||||||||
левую отсеченную часть фермы (рис. 1, г), определим усилие N3−10 |
из условия |
||||||||||
равновесия |
|
|
|
|
|
|
|
|
|
|
|
|
∑m(0) = −F (24 +26 + 28 +30 +32) +VA 28 − N3−10 32 − |
|
|||||||||
|
|
−N22−10 sinβ 30 + N22−10 cosβ 1,75 =0; N3−10 |
=18,16 кН. |
(1) |
|||||||
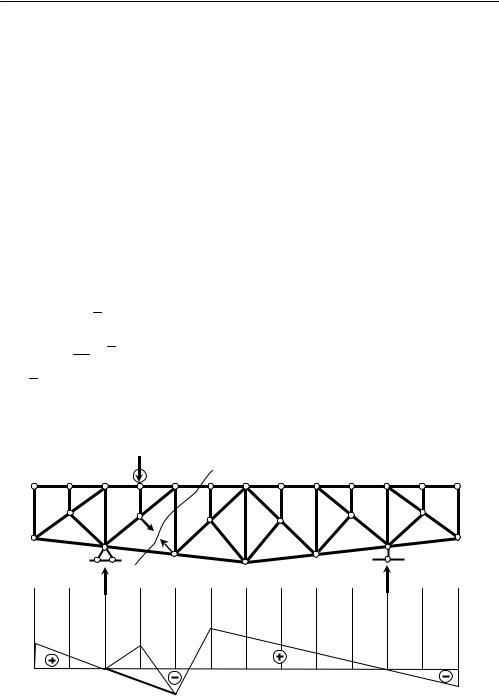
Для построения линии влияния усилия в стойке |
N3−10 поступим анало- |
||||||||||
гичным образом. Проведем сечение I-I (рис. 2). При составлении уравнений |
|||||||||||
равновесия для левой и правой частей фермы относительно моментной точки |
|||||||||||
O , усилие в стержне N22−10 |
не учитываем, |
т. к. оно отлично от нуля только |
|||||||||
при положении единичной силы в узле 16 грузового пояса. Из уравнения рав- |
|||||||||||
новесия (1) находим ординату линии влияния под узлом 16: |
|
||||||||||
∑m(0) =− F 30 +VA 28 − N3−10 32 − N22−10 sinβ 30 + N22−10 cosβ 1,75 =0; |
|||||||||||
N3−10 = |
|
1 |
(−F 30 +VA 28 − N22−10 sinβ 30 + N22−10 cosβ 1,75) = |
0,329, |
|||||||
|
32 |
|
|
|
|
|
|
|
|
|
|
где F =1 – величина подвижной силы; N22−10 = −0,752 – усилие в стержне при |
|||||||||||
загружении узла 16; VA =0,875 |
– ордината под узлом 16 на линии влияния |
||||||||||
опорной реакции (на рис. 2 не показана). |
|
|
|
|
|
||||||
|
|
|
F = 1 |
|
I |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
N22-10 |
10 |
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N22-10 |
|
|
Линия влияния N3- |
VB |
|
|||
|
|
|
VA |
|
|
|
|
|
|
|
|
|
|
|
|
0,547 |
|
|
|
|
|
|
|
0,344 |
|
0,172 |
0,329 |
|
0,438 |
0,328 |
0,219 |
|
0,109 |
|
|
|
|
|
|
0,344 |
|
|
|
|
|
0,109 |
0,219 |
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
Для проверки определим усилие в стержне от постоянной нагрузки по |
|||||||||||
построенной линии влияния |
|
|
|
|
|
|
|
|
|||
88 |
Материалы 57-й научно-технической конференции |
N3−10 = F(0,344 +0,172 +0,329 −0,344 +0,547 +0,438 +0,329 +0,219 − +0,109 −0,109 −0,219) =10 1,815 =18,15 кН.
Таким образом, предложен способ расчета шпренгельных ферм, не требующий разделения фермы на основную ферму и шпренгели.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Строительная механика. Статика упругих систем : учеб. для вузов /В.Д. Потапов, А.В. Александров [и др.]. – М. : Высшая школа, 2007. – 511 с.
УДК 666.97.031:66.093+537.84
Е.Ю. ЩЕПТИНОВ, студент гр. 136/2 Научный руководитель:
В.Н. САФРОНОВ, канд. техн. наук, профессор
КАЧЕСТВО БЕТОННОЙ СМЕСИ И МЕЛКОЗЕРНИСТОГО БЕТОНА
ПРИ ПРИМЕНЕНИИ ЦИКЛОВОЙ МАГНИТНОЙ АКТИВАЦИИ ВОДЫ ЗАТВОРЕНИЯ С ДОБАВКОЙ НА ОСНОВЕ ЛИГНОСУЛЬФОНАТА
Впоследнее время развитие бетоноведения стремится к получению высококачественных конкурентноспособных бетонов, таким образом происходит постепенное замещение обычных бетонов многокомпонентными. В таких бетонах используется как индивидуальные химические модификаторы, улучшающие удобоукладываемость бетонных смесей и, способствующих повышению физико-механических показателей бетона, так и комплексные добавки, включающие зачастую до нескольких десятков индивидуальных химических добавок различного функционального назначения. Параллельно с этим, широкое развитие получают электрофизические технологии активации компонентов бетона, связанные с совершенствованием как отдельных составляющих бетона, так и бетонной смеси и самого бетона.
ВТГАСУ на кафедре СМиТ разработана технология цикловой магнитной обработки воды затворения и для повышения эффективности магнитной активации была предложена технология, включающая в себя магнитную обработку воды с разбавленным в ней суперпластификатором. В качестве суперпластификатора использовалась водная суспензия на основе лигносульфоната в количестве 0,8 % от массы цемента. Проведены экспериментальные исследования прочности цементного камня при использовании данной технологии на цементе М500-Д0, результаты приведены в табл. 1.
При принятом водоцементном отношении равном 0,3, наблюдалось хорошая удобоукладываемость цементного теста, не требующее дополнительного уплотнения. Максимум прочности активированных образцов составлял 91,8 МПа при количестве циклов активации равном 20. Контрольный состав
