Зубчатые передачи Общие положения

Зубчатые передачи предназначены для передачи вращательного движения от одного вала к другому, а также для изменения величины и направления угловой скорости валов. Пару зубчатых колес, находящихся в зацеплении друг с другом, называют ступенью.

Все зубчатые одноступенчатые передачи можно разделить на цилиндрические, конические и гиперболоидные.

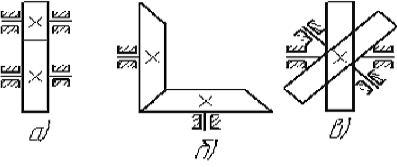
Кинематические схемы зубчатых передач: а – цилиндрическая;

б – коническая; в – гиперболоидная

По характеру расположения осей вращения передачи бывают с параллельными, пересекающимися и перекрещивающимися осями.

В цилиндрических передачах оси валов параллельны. По характеру расположения зубьев на зацепляющихся колесах они разделяются на прямозубые, косозубые и шевронные.

В конических передачах оси валов пересекаются. Наиболее распространены конические передачи с прямым углом между осями валов.

В гиперболоидных передачах оси валов перекрещиваются. В свою очередь эти передачи подразделяются на гипоидные, винтовые и червячные. Последние являются частным случаем винтовых передач и состоят из червяка и червячного колеса.

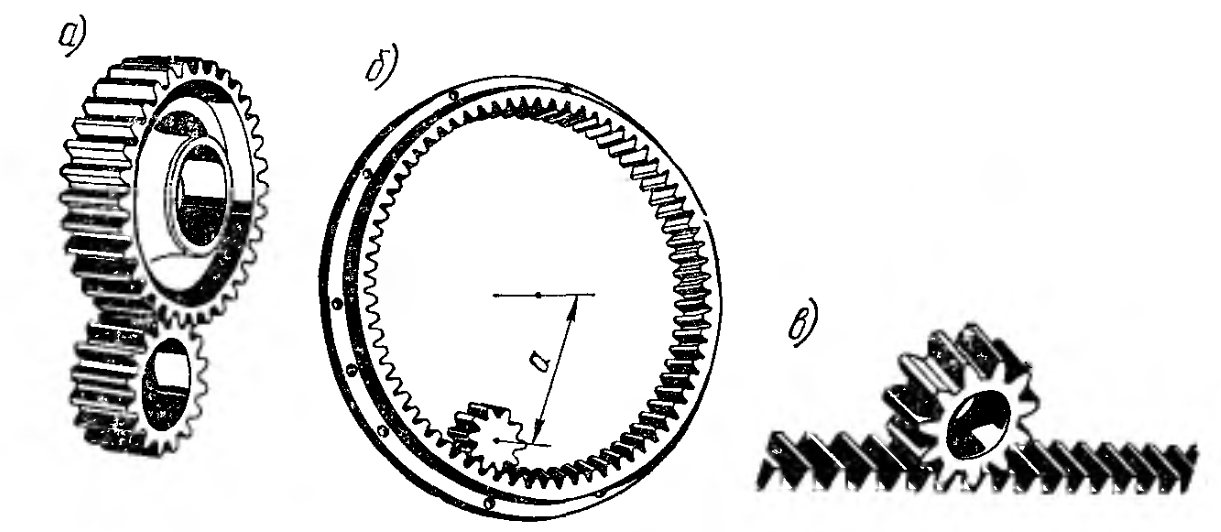
Прямозубые передачи

а – с наружным зацеплением

б – с внутренним зацеплением

в – реечная передача

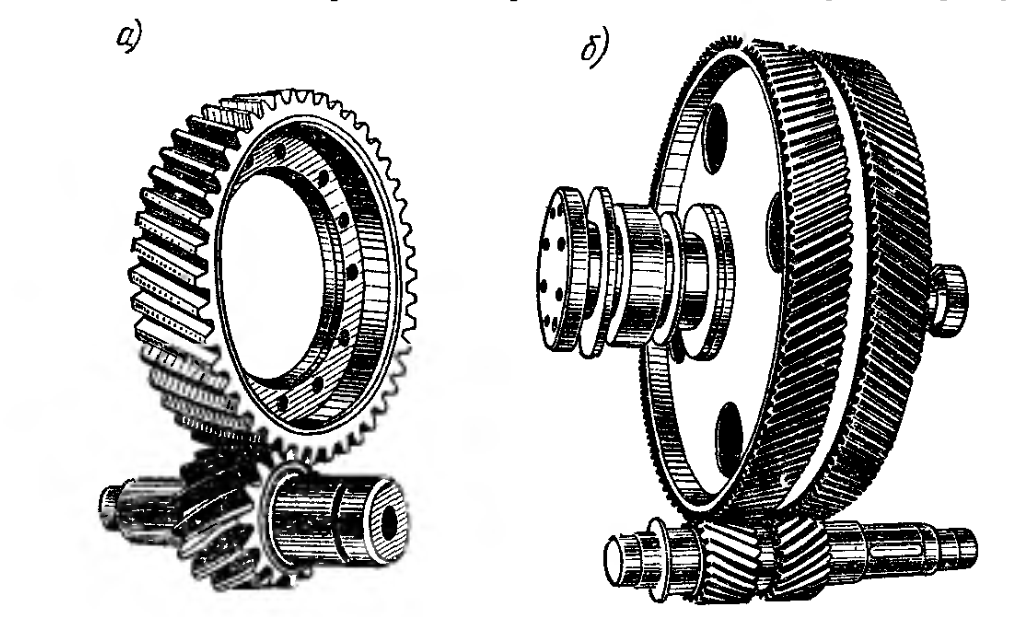
а – косозубая передача

б – шевронная передача

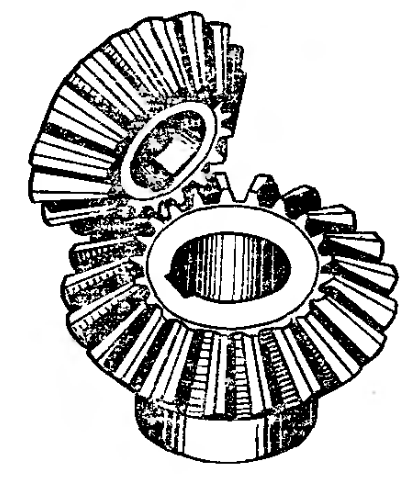
Коническая передача

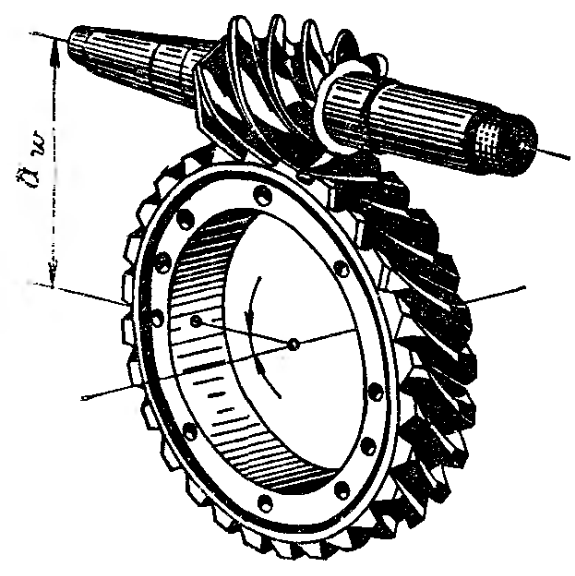
Червячная передача

Преимуществами зубчатых передач перед другими (фрикционными, ременными, цепными) являются постоянство передаточного отношения, высокий механический кпд, долговечность и компактность.

Недостатком является то, что наличие высшей кинематической пары в месте контакта зубьев приводит к большим контактным напряжениям, тем самым при их эксплуатации приходится ограничивать величину передаваемых усилий, упрочнять поверхности зубьев в зоне их контакта, применять систему смазки колес.

Передаточное отношение

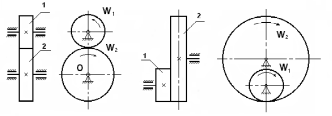
Передаточное отношение – это отношение угловых скоростей взаимодействующих (зацепляющихся) зубчатых колес. Если взаимо-действие колес внешнее, то их передаточное отношение отрицательно (U_1-2 < 0), (рис. 5.2), если взаимодействие внутреннее, то U_1-2 > 0 (рис. 5.3). Знак «+» указывает на совпадение векторов угловых скоростей (направлений вращения колес).

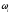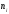Численно величина передаточного отношения ступени равна отношению угловых скоростей , (1/с), частот вращений, (об/мин), или обратному отношению количества зубьев колес: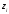

.

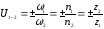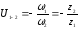
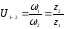
Пара зубчатых колес с внешним зацеплением: 1, 2 – зубчатые колеса

Пара зубчатых колес с внутренним зацеплением: 1, 2 – зубчатые колеса

Передаточное отношение сложных (многоступенчатых) зубчатых передач (рис. 5.4) равно произведению передаточных отношений ступеней:

,

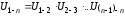где 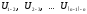– передаточные отношения ступеней.

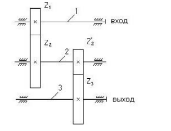
Двухступенчатая зубчатая передача

Например, для двухступенчатой зубчатой передачи, кинематическая схема которой представлена на рис. величина передаточного отношения

.

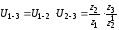Основные геометрические параметры зубчатого колеса цилиндрической передачи

Рассмотрим геометрические параметры зубчатого колеса цилиндрической передачи в плоскости, перпендикулярной оси его вращения.

Каждый зуб колеса имеет ось симметрии, проходящую через ось вращения колеса О. Угол между осями симметрии называется угловым шагом τ. Число зубьев колеса z=2π/τ (если τ измеряется в радианах) или z=360º/ τ (если τ измеряется в угловых градусах). Внешняя граница зуба очерчивается окружностью выступов радиусом r_a, а внутренняя часть впадины – окружностью впадин радиусом r_f.

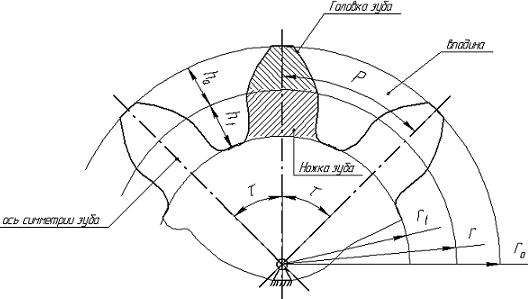
Геометрические параметры зубчатого колеса

Окружность радиусом r делит зуб по высоте на головку и ножку. Расстояние между одноименными профилями соседних зубьев по дуге этой окружности (или между соседними осями симметрии зубьев) называется окружным шагом P.

Длина окружности диаметром d=2 π r

L=Pz= πd,

откуда

d=(P/π)×z.

Величину P/π = m называют модулем. На него введен ГОСТ 9563-60, в соответствии с которым при расчетах геометрических параметров зуб-чатых колес его выбирают из стандартного ряда в пределах m = 0,05…100 мм.

Окружность, по которой модуль m является стандартной величиной, называется делительной окружностью с диаметром d = m×z или радиусом r = (m×z)/2.

Все остальные геометрические параметры зубчатого колеса в соответствии с ГОСТом пропорциональны модулю m:

высота головки зуба h_a = m;

высота ножки зуба h_f = 1,25 m;

высота зуба h = h_a+h_f = 2,25 m;

радиус окружности выступов

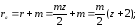
радиус окружности впадин

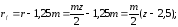
окружной шаг P=π×m;

толщина зуба по делительной окружности

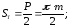
ширина впадин по делительной окружности

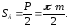
Ширину колеса принимают в пределах в = (10…30)m. Межосевое расстояние двух зацепляющихся колес нулевого зацепления

,

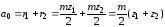где r₁ и r₂ – радиусы делительных окружностей зацепляющих колес; z₁ и z₂ – число их зубьев.

В зацепление друг с другом могут входить только зубчатые колеса, имеющие одинаковый модуль m и окружной шаг P.

29