Задача 3.1.

Задана структурная схема для расчёта надёжности системы, по известным интенсивностям отказов её элементов (таблица 1) предполагая, что отказы элементов распределены по экспоненциальному закону. Определить:

• вероятность безотказной работы системы;

• интенсивность отказа узла системы;

• среднее время наработки до первого отказа узла системы.

Таблица 1-Интенсивности отказов элементов

номер варианта	интенсивность отказа элементов
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
24	3,19	5,25	4,61	1,88	1,88	0,78	1,87	6,52	0,98	0,85	4,35	4,35	1,89	1,89	-

t=2 года=17520ч

Узлы в системе можно представить, с точки зрения надежности, как последовательно так и параллельно соединенные элементы.

Так, например вероятность безотказной работы последовательно соединенных элементов можно определить как произведение вероятностей безотказной работы каждого элемента:

P_c(t)=P₁(t)*P₂(t) а вероятность отказа q_c(t)=1-P_c(t) = 1- P₁(t)*P₂(t)

А вероятность безотказной работы параллельно соединенных элементов можно найти так:

q_c(t)= q₁(t)*q₂(t); P_c(t)=1- q_c(t); P_c(t)=1- (1- P₁(t))(1- P₂(t))

Вероятность безотказной работы i элемента можно найти по формуле:

Если воспользоваться вышеуказанными правилами вычисления вероятностей безотказной работы для последовательно и параллельно соединенных элементов, то вероятность безотказной работы узла системы (обведенного пунктиром) можно найти по формуле:

,где - вероятности безотказной работы 10-14 элементов соответственно.

Для верхней ветви системы:

В узле «с» кратность общего резервирования замещением m=1, тогда используем следующую формулу:

, где - интенсивность отказов основной системы;-интенсивность отказов резервной системы.

В данном случае:

Вероятность безотказной работы системы:

Среднее время работы до первого отказа узла системы:

(если время возникновения отказов подчиненного экспоненциальному закону).

Упростим выражение:

Упростим следующее выражение:

Интеграл принимает вид:

Продолжим преобразование подынтегрального выражения:

Интеграл вида имеет первообразную:

Учитывая полученный результат определим :

Определим интенсивность отказов узла I:

Частота отказов узла системы может быть найдена по формуле:

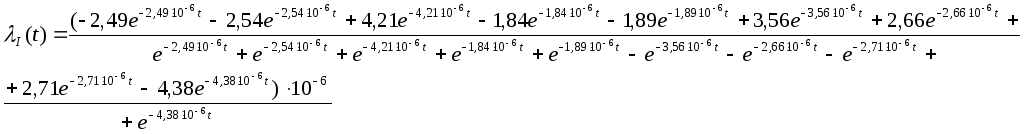
Задача №3.2.

Система содержит n групп элементов, каждая j – группа, в свою очередь, содержит N_j элементов, причем λ_j – интенсивность отказов элементов j – группы. Вероятность безотказной работы системы за время t равна Р_к(t). Требуется определить число элементов ЗИПа. Исходные данные приведены в таблице.

№ Вар	Рк(t)	t,ч	n	Реле		Резисторы		Конденсаторы		Диоды		Транзисторы
				N1	λ1*10-5	N2	λ2*10-5	N3	λ3*10-6	N4	λ4*10-6	N5	λ5*10-6
22	0,92	17000	5	20	1,4	36	0,2	36	1,6	28	2,5	40	0,95

Определим интенсивности отказов групп элементов:

Определим вероятность безотказной работы групп элементов:

Определим вероятность безотказной работы системы при последовательном соединении без ЗИПа:

Определим коэффициент ЗИПа:

Для холодного ЗИПа справедливо выражение:

_{Число запасных элементов m определяется подбором, при условии}

Определим число элементов ЗИПа для реле:

Подбором установлено m≥8

Определим число элементов ЗИПа для резисторов:

Подбором установлено m≥3

Определим число элементов ЗИПа для конденсаторов:

Подбором установлено m≥2

Определим число элементов ЗИПа для диодов:

Подбором установлено m≥3

Определим число элементов ЗИПа для транзисторов:

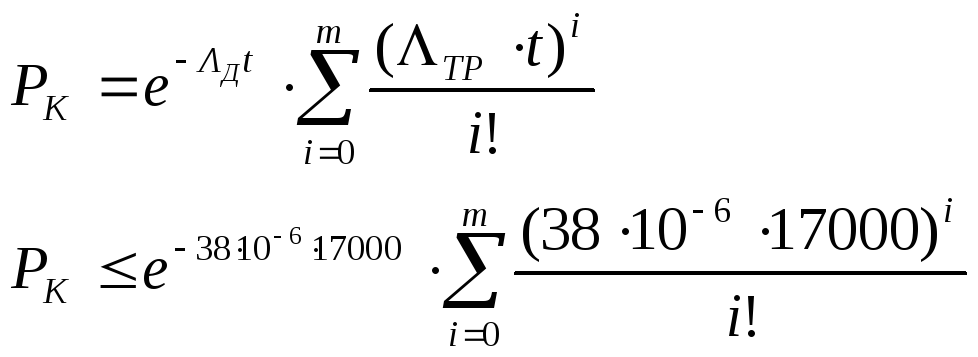
Подбором установлено m≥2