
- •Теория автоматического управления и регулирования
- •2005 Введение
- •1. Общие сведения о системах автоматического регулирования
- •1.1. Основные задачи
- •1.2. Понятие об автоматическом регулировании
- •1.3. Разомкнутые и замкнутые системы автоматического регулирования
- •1.4. Системы автоматической стабилизации
- •1.5. Следящие системы
- •1.6. Понятие о непрерывных и прерывистых системах
- •Контрольные вопросы
- •2. Линейные и нелинейные системы автоматического регулирования. Общий метод линеаризации
- •2.1. Общие положения
- •2.2. Общий метод линеаризации
- •Контрольные вопросы
- •3. Динамические звенья и их характеристики
- •3.1. Общие положения
- •3.2. Временные характеристики звеньев
- •3.3. Частотные характеристики звеньев
- •3.4. Логарифмические частотные характеристики звеньев
- •3.5. Безынерционное звено
- •3.6. Апериодическое звено первого порядка
- •3.7. Апериодическое звено второго порядка
- •3.8. Идеальное интегрирующее звено
- •3.9. Инерционное интегрирующее звено
- •3.10. Идеальное дифференцирующее звено
- •3.11. Реальное дифференцирующее звено
- •3.12. Неустойчивые звенья
- •Контрольные вопросы
- •4. Составление и анализ исходных дифференциальных уравнений Систем Автоматического регулирования
- •4.1. Общий метод составления исходных уравнений
- •4.2. Передаточные функции систем автоматического регулирования
- •4.3. Составление уравнений на основе типовых звеньев
- •Контрольные вопросы
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Понятие об устойчивости линейных систем
- •5.2. Алгебраический критерий устойчивости
- •1. Уравнение первого порядка
- •2. Уравнение второго порядка
- •3. Уравнение третьего порядка
- •4. Уравнение четвертого порядка
- •5.3. Критерий устойчивости Михайлова
- •5.4. Определение устойчивости по логарифмическим характеристикам
- •Контрольные вопросы
- •6. Построение кривой переходного процесса в системе автоматического регулирования
- •6.1. Общие положения
- •6.2. Классический метод
- •6.3. Метод трапецеидальных вещественных характеристик
- •Контрольные вопросы
- •7. Оценка качества регулирования
- •7.1. Общие положения
- •7.2. Точность в типовых режимах
- •7.3. Определение показателей качества регулирования по переходной характеристике
- •7.4. Приближенная оценка вида переходного процесса по вещественной частотной характеристике
- •7.5. Корневые методы
- •7.6. Частотные критерии качества
- •Контрольные вопросы
- •8. Элементы синтеза систем автоматического регулирования
- •8.1. Общие положения
- •8.2. Метод логарифмических амплитудных характеристик
- •8.3. Синтез последовательного корректирующего устройства
- •Контрольные вопросы
- •9. Нелинейные Системы автоматического регулирования
- •9.1. Методы исследования процессов в нелинейных системах
- •9.2. Метод фазовой плоскости
- •Контрольные вопросы
- •Заключение
- •Рекомендуемый Библиографический список
2. Линейные и нелинейные системы автоматического регулирования. Общий метод линеаризации
2.1. Общие положения
Динамические процессы в системах регулирования описываются дифференциальными уравнениями.
В линейных системах процессы описываются при помощи линейных дифференциальных уравнений. В нелинейных системах процессы описываются уравнениями, содержащими какие-либонелинейности. Расчеты линейных систем хорошо разработаны и более просты для практического применения. Расчеты же нелинейных систем часто связаны с большими трудностями.
Чтобы система регулирования была линейной, необходимо (но недостаточно) иметь статические характеристики всех звеньев в виде прямых линий. В действительности реальные статические характеристики в большинстве случаев не являются прямолинейными. Поэтому, чтобы рассчитать реальную систему как линейную, необходимо все криволинейные статические характеристики звеньев на рабочих участках, которые используются в данном процессе регулирования, заменить прямолинейными отрезками. Это называется линеаризацией. Большинство систем непрерывного регулирования поддаётся такой линеаризации.
Линейные системы разделяются на обыкновенные линейные системыи наособые линейные системы.К первым относятся такие системы, все звенья которых описываются обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами.
К особым линейным системам относятся:
а) системы с переменными по времени параметрами, которые описываются линейными дифференциальными уравнениями с переменными коэффициентами;
б) системы с распределёнными параметрами, где приходится иметь дело с уравнениями в частных производных, и системы с временным запаздыванием, описываемые уравнениями с запаздывающим аргументом;
в) импульсные системы, где приходится иметь дело с разностными уравнениями.
В нелинейных системах при анализе процесса регулирования приходится учитывать нелинейность статической характеристики хотя бы в одном её звене или какие-то нелинейные дифференциальные зависимости в уравнениях динамики системы. Иногда нелинейные звенья специально вводятся в систему для обеспечения наибольшего быстродействия или других желаемых качеств.
К нелинейным системам относятся прежде всего релейные системы, так как релейная характеристика(рис. 2.1,аиб) не может быть заменена одной прямой линией. Нелинейным будет звено, в характеристике которого имеетсязона нечувствительности(рис. 2.1,в).
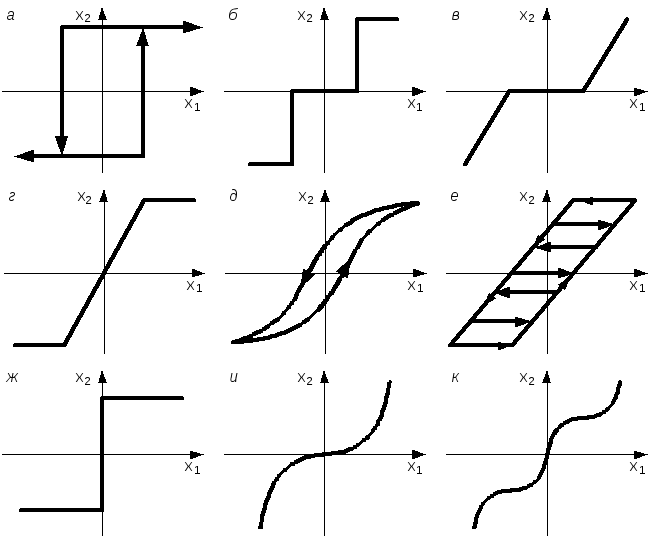
Рис. 2.1. Характеристики нелинейных элементов
Явления насыщенияилимеханического ограничения ходаприводят кхарактеристике с ограничением линейной зависимости на концах (рис. 2.1, г).Эта характеристика также должна считаться нелинейной, если рассматриваются такие процессы, когда рабочая точка выходит за пределы линейного участка характеристики.
К нелинейным зависимостям относятся также гистерезисная кривая(рис. 2.1,д), характеристиказазора в механической передаче(рис. 2.1, е),сухое трение(рис. 2.1,ж),квадратичное трение(рис. 2.1,и) и др. В последних двух характеристиках x1обозначает скорость перемещения, а x2– силу или момент трения.
Нелинейной является вообще любая криволинейная зависимость между выходной и входной величинами звена (рис. 2.1, к). Это нелинейности простейшего типа. Кроме того, нелинейности могут входить в дифференциальные уравнения в виде произведения переменных величин и их производных, а также в виде более сложных функциональных зависимостей.
Не все нелинейные зависимости поддаются простой линеаризации. Так, например, линеаризация не может быть сделана для характеристик, изображенных на рис. 2.1, а или на рис. 2.1, е. Подобные сложные случаи будут рассмотрены в разд. 9.
