
- •Теория автоматического управления и регулирования
- •2005 Введение
- •1. Общие сведения о системах автоматического регулирования
- •1.1. Основные задачи
- •1.2. Понятие об автоматическом регулировании
- •1.3. Разомкнутые и замкнутые системы автоматического регулирования
- •1.4. Системы автоматической стабилизации
- •1.5. Следящие системы
- •1.6. Понятие о непрерывных и прерывистых системах
- •Контрольные вопросы
- •2. Линейные и нелинейные системы автоматического регулирования. Общий метод линеаризации
- •2.1. Общие положения
- •2.2. Общий метод линеаризации
- •Контрольные вопросы
- •3. Динамические звенья и их характеристики
- •3.1. Общие положения
- •3.2. Временные характеристики звеньев
- •3.3. Частотные характеристики звеньев
- •3.4. Логарифмические частотные характеристики звеньев
- •3.5. Безынерционное звено
- •3.6. Апериодическое звено первого порядка
- •3.7. Апериодическое звено второго порядка
- •3.8. Идеальное интегрирующее звено
- •3.9. Инерционное интегрирующее звено
- •3.10. Идеальное дифференцирующее звено
- •3.11. Реальное дифференцирующее звено
- •3.12. Неустойчивые звенья
- •Контрольные вопросы
- •4. Составление и анализ исходных дифференциальных уравнений Систем Автоматического регулирования
- •4.1. Общий метод составления исходных уравнений
- •4.2. Передаточные функции систем автоматического регулирования
- •4.3. Составление уравнений на основе типовых звеньев
- •Контрольные вопросы
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Понятие об устойчивости линейных систем
- •5.2. Алгебраический критерий устойчивости
- •1. Уравнение первого порядка
- •2. Уравнение второго порядка
- •3. Уравнение третьего порядка
- •4. Уравнение четвертого порядка
- •5.3. Критерий устойчивости Михайлова
- •5.4. Определение устойчивости по логарифмическим характеристикам
- •Контрольные вопросы
- •6. Построение кривой переходного процесса в системе автоматического регулирования
- •6.1. Общие положения
- •6.2. Классический метод
- •6.3. Метод трапецеидальных вещественных характеристик
- •Контрольные вопросы
- •7. Оценка качества регулирования
- •7.1. Общие положения
- •7.2. Точность в типовых режимах
- •7.3. Определение показателей качества регулирования по переходной характеристике
- •7.4. Приближенная оценка вида переходного процесса по вещественной частотной характеристике
- •7.5. Корневые методы
- •7.6. Частотные критерии качества
- •Контрольные вопросы
- •8. Элементы синтеза систем автоматического регулирования
- •8.1. Общие положения
- •8.2. Метод логарифмических амплитудных характеристик
- •8.3. Синтез последовательного корректирующего устройства
- •Контрольные вопросы
- •9. Нелинейные Системы автоматического регулирования
- •9.1. Методы исследования процессов в нелинейных системах
- •9.2. Метод фазовой плоскости
- •Контрольные вопросы
- •Заключение
- •Рекомендуемый Библиографический список
3.10. Идеальное дифференцирующее звено
Звено описывается уравнением
![]() (3.74)
(3.74)
или в операторной форме
![]() .
(3.75)
.
(3.75)
Передаточная функция
![]() .
(3.76)
.
(3.76)
Примеры идеальных дифференцирующих звеньев изображены на рис. 3.25. Единственным идеальным дифференцирующим звеном, которое точно описывается уравнением (3.74), является тахогенератор постоянного тока (рис. 3.25, а), если в качестве входной величины рассматривать угол поворота его ротора, а в качестве выходной – напряжение якоря U. Приближенно в качестве идеального дифференцирующего звена может рассматриваться операционный усилитель в режиме дифференцирования (рис. 3.25,б).
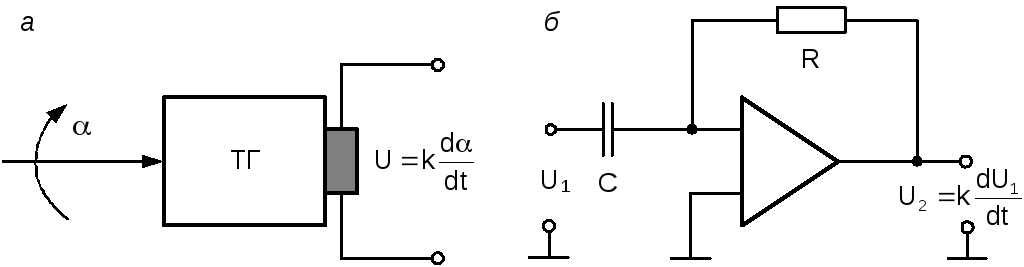
Рис. 3.25. Идеальные дифференцирующие звенья
Рис. 3.26. Переходная
функция идеального дифференцирующего
звена 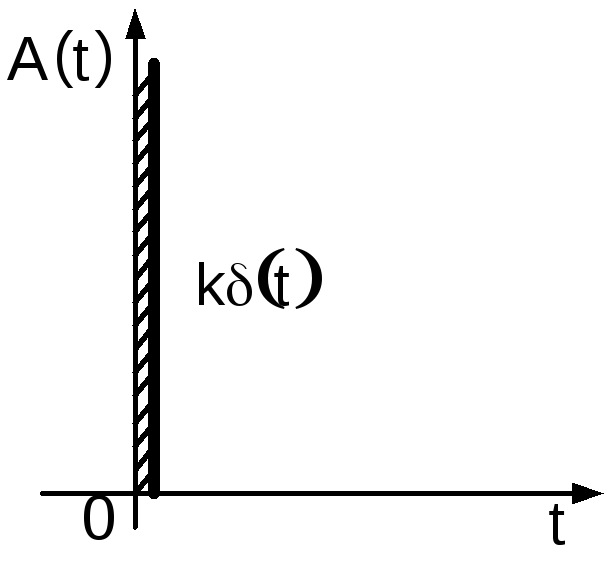
Переходная функция звена при х1= 1(t);A(t) = k 1’(t) = k (t) представляет собой импульсную функцию, площадь которой равнаk(рис. 3.26). Функция веса представляет собой импульсную функцию второго порядка.
Частотная передаточная функция, её модуль и фаза соответственно равны
w(j) = kj;(3.77)
A() = k; = +900при > 0; = -900при < 0. (3.78)
Частотные характеристики изображены на рис. 3.27.
Из амплитудной характеристики видно, что звено пропускает сигнал тем сильнее, чем выше его частота. Это свойство является в автоматических системах часто нежелательным, так как звено может в значительной степени повышать уровень действующих в системе помех, которые, как правило, являются высокочастотными.
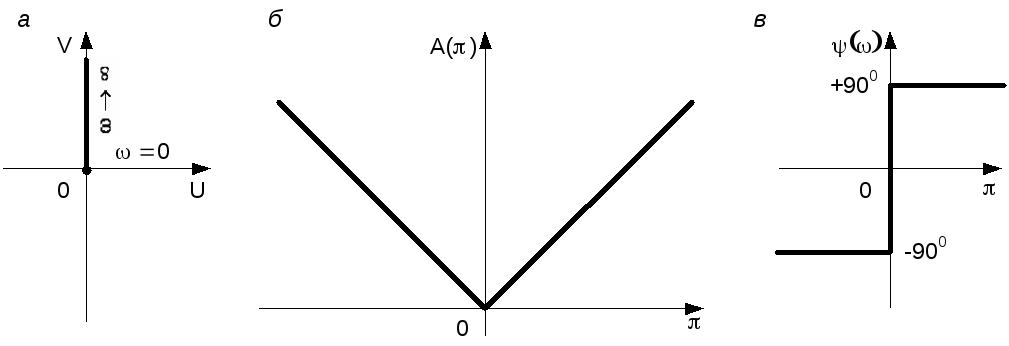
Рис. 3.27. АФЧХ (а), АЧХ (б) и ФЧХ (в) идеального дифференцирующего звена
Амплитудно-фазовая характеристика для положительных частот сливается с положительным направлением оси мнимых.
ЛАХ строится по выражению
![]() . (3.79)
. (3.79)
Нетрудно видеть, что ЛАХ представляет
собой прямую с положительным наклоном
20 дБ/дек (рис. 3.28). Эта прямая пересекает
ось нуля децибел при частоте среза
![]() .
.
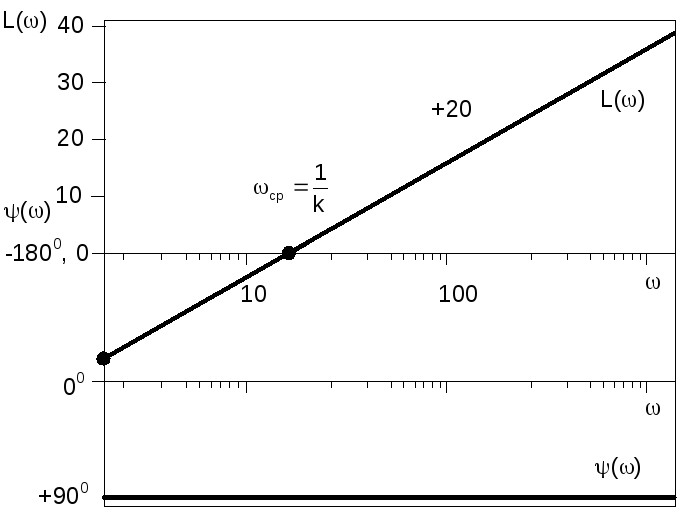
Рис. 3.28. ЛАХ и ЛФХ идеального дифференцирующего звена
ЛФХ представляет собой прямую линию = +900, параллельную оси частот.
3.11. Реальное дифференцирующее звено
Звено описывается уравнением
![]() . (3.80)
. (3.80)
Передаточная функция звена
![]() .
(3.81)
.
(3.81)
Звено условно можно представить в виде двух включенных последовательно звеньев – идеального дифференцирующего звена и апериодического звена первого порядка.
На рис. 3.29 изображены примеры реальных дифференцирующих звеньев: дифференцирующая RC-цепь (рис. 3.29, а), RL-цепь (рис. 3.29,б) и дифференцирующий трансформатор (рис. 3.29,в).
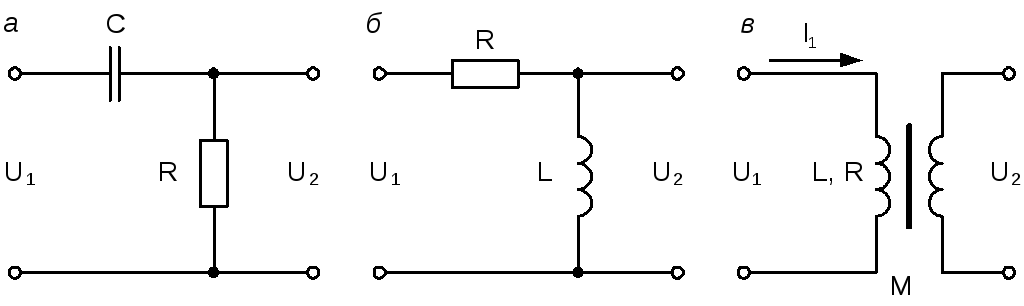
Рис. 3.29. Реальные дифференцирующие звенья
Переходная функция определяется решением (3.80) при х1 = 1(t) и нулевых начальных условиях
![]() .
(3.82)
.
(3.82)
Функция веса
![]() .
(3.83)
.
(3.83)
Временные характеристики изображены на рис. 3.30. Там же показаны построения, позволяющие по экспериментальным характеристикам определять параметры звена.
Частотная передаточная функция, её модуль и фаза соответственно равны:
![]() ; (3.84)
; (3.84)
![]() (3.85)
(3.85)
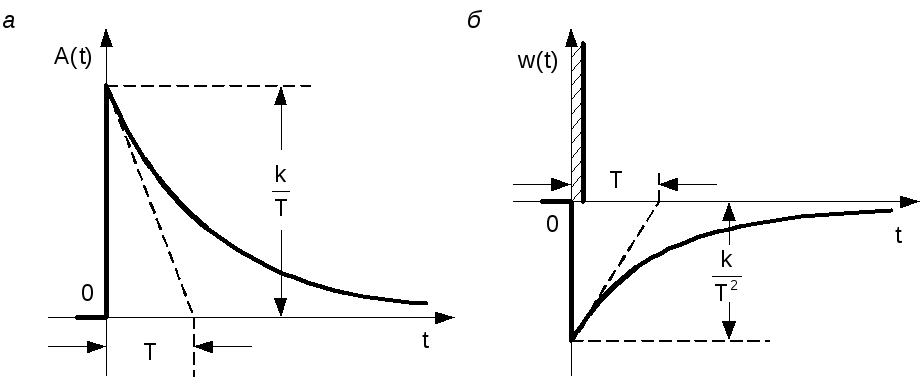
Рис. 3.30. Переходная функция (а) и дельта-функция (б) реального дифференцирующего звена
Амплитудная, фазовая и амплитудно-фазовая характеристики звена изображены на рис. 3.31.
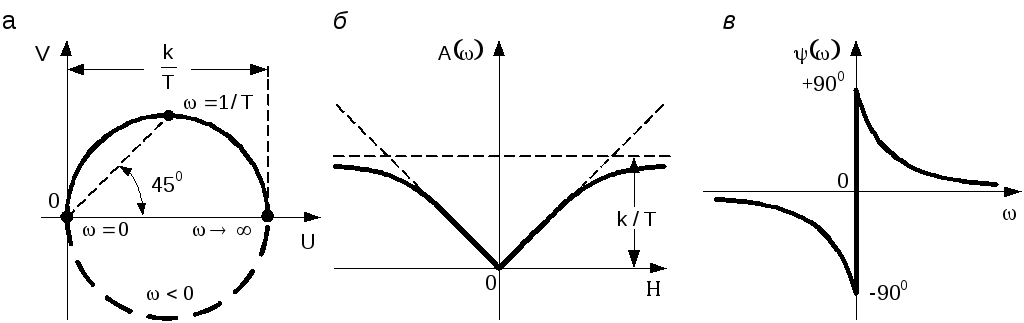
Рис. 3.31. АФЧХ (а), АЧХ (б) и ФЧХ (в) реального дифференцирующего звена
Амплитудная
характеристика реального звена отличается
от амплитудной характеристики идеального
дифференцирующего звена (показана
пунктиром). Характеристики совпадают
в области низких частот. В области
высоких частот реальное звено пропускает
сигнал хуже, чем идеальное звено.
Коэффициент передачи стремится к
значению k / T
при
![]() .
Для звеньев, представляющих собой RC-
или RL-цепь (см. рис. 3.29), коэффициент k / T
= 1, и на высоких частотах коэффициент
передачи стремится к единице.
.
Для звеньев, представляющих собой RC-
или RL-цепь (см. рис. 3.29), коэффициент k / T
= 1, и на высоких частотах коэффициент
передачи стремится к единице.
Это означает, что в дифференцирующей RC-цепи конденсатор имеет сопротивление, стремящееся к нулю, а в дифференцирующей RL-цепи индуктивность имеет сопротивление, стремящееся к бесконечности. И в том, и в другом случаях напряжение на выходе будет равно напряжению на входе.
Фазовые сдвиги, вносимые звеном, являются
наибольшими при низких частотах. На
высоких частотах фазовый сдвиг постепенно
уменьшается, стремясь в пределе к нулю
при
![]() .
Здесь также видно, что реальное звено
ведет себя подобно идеальному только
в области низких частот.
.
Здесь также видно, что реальное звено
ведет себя подобно идеальному только
в области низких частот.
Амплитудно-фазовая характеристика для
положительных частот представляет
собой полуокружность с диаметром, равным
k/T. На
полуокружности нанесены характерные
точки:![]() .
Дополнив эту полуокружность её зеркальным
изображением относительно вещественной
оси, получим полную амплитудно-фазовую
характеристику для всех частот, лежащих
в пределах
.
Дополнив эту полуокружность её зеркальным
изображением относительно вещественной
оси, получим полную амплитудно-фазовую
характеристику для всех частот, лежащих
в пределах![]() .
.
ЛАХ строится по выражению
![]() .
(3.86)
.
(3.86)
Для построения асимптотической ЛАХ
(рис. 3.32) проведем вертикальную линию
при сопрягающей частоте
![]() .
.
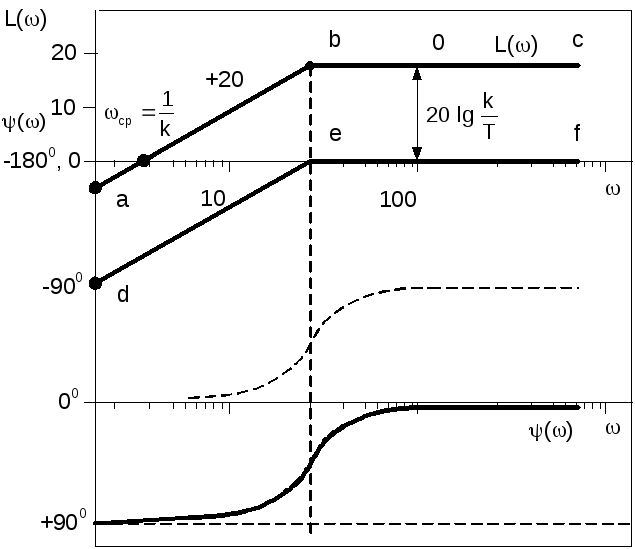
Рис. 3.32. ЛАХ и ЛФХ реального дифференцирующего звена
Левее этой линии, то есть при
![]() ,
можно воспользоваться приближенным
выражением
,
можно воспользоваться приближенным
выражением![]() .
Этому выражению соответствует прямая
линия с положительным наклоном 20 дБ/дек
(прямая а–b). Она может
быть построена, например, по частоте
среза
.
Этому выражению соответствует прямая
линия с положительным наклоном 20 дБ/дек
(прямая а–b). Она может
быть построена, например, по частоте
среза![]() .
.
Для частот
![]() можно пользоваться приближенным
выражением
можно пользоваться приближенным
выражением![]() .
Этому выражению соответствует прямая,
параллельная оси частот (b– с). Действительная ЛАХ отличается от
асимптотической в точке излома «b»
на величину 3 дБ.
.
Этому выражению соответствует прямая,
параллельная оси частот (b– с). Действительная ЛАХ отличается от
асимптотической в точке излома «b»
на величину 3 дБ.
На рис. 3.32 показана асимптотическая ЛАХ для случая k = 1 (ломаная прямая d–e–f).
ЛФХ строится по второму уравнению
системы (3.85). Для этого сначала строится
первое слагаемое 1= +900,
а затем второе2= –аrctg ωТ.
Результирующая ЛФХ показана сплошной
линией. При![]() фазовый сдвиг равен +450.
фазовый сдвиг равен +450.
