- •4. Полярная система координат на плоскости.
- •5. Прямоугольные декартовые координаты пространств.
- •9. Угол между двумя прямыми. Расстояние от точки до прямой.
- •10. Линии второго порядка. Окружность.
- •11.Линии второго порядка.Эллипс
- •12. Линии второго порядка.Гипербола.
- •13 Линии второго порядка. Парабола
- •14 .Основные понятия и определения. Теория матрицы
- •15. Линейные действия над матрицами
- •16.Произведение матриц
- •17.Транспонировние матрицы
- •18. Определители 2-ого и 3-ого порядков.
- •19. Обратная матрица
- •20. Ранг матрицы
- •21. Система линейных уравнений. Основные понятия
- •22.Решение систем линейных уравнений с помощью определителя(теорема Крамера)
- •23. Исследование систем линейных уравнений (теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)
- •24.Матричный метод решения систем линейных уравнений
- •25)Метод Гаусса решения систем линейных уравнений.
- •29.Умножение вектора на число. Свойства линейных операций над векторами.
- •31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
- •Вопрос32. Разложение вектора по базису
- •Вопрос33.Прямоугольные декартовы координаты в пространстве
- •34. Длина вектора. Линейные операции над векторами в прямоугольных координатах: сумма, разность, умножение на число. Признак коллинеарности двух векторов в прямоугольных координатах.
- •35. Скалярное произведение векторов
- •37.Смешанное произведение 3 векторов.
- •38. Линейная зависимость векторов
- •39.Уравнение поверхности и линии
- •Уравнение плоскости, проходящей через три точки
- •41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки
- •44. Понятие сложной функции. Четные и нечетные функции, переодические функции.Основные элементарные функции.
- •45. Функция натурального аргументы и ее предел.
- •47. Предел функции в точке и на бескон. Определение
- •49. Основныесв-ва пределов функций.
- •50.Замечательные пределы
- •51. Непрерывные ф-ции.Точки разрыва ,их классификация.
34. Длина вектора. Линейные операции над векторами в прямоугольных координатах: сумма, разность, умножение на число. Признак коллинеарности двух векторов в прямоугольных координатах.
Длина
a
вектора
 (а1,
а2,
а3)
вычисляется,
(а1,
а2,
а3)
вычисляется,

Пусть в пространстве
введена прямоугольная система координат в которой векторы
в которой векторы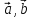 имеют координаты
имеют координаты (1),тогда
(1),тогда
Признаком
коллинеарности векторов является
пропорционально их координат, при этом
 ,
имеем
,
имеем ,
,
Сложение векторов
По правилу
треугольника: если данный два вектора
 ,
то вектор
,
то вектор откладываем
от любой точки А пространства
откладываем
от любой точки А пространства .
Затем от конца В вектора
.
Затем от конца В вектора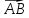 откладываем вектор
откладываем вектор .
Суммой
.
Суммой векторов
векторов и
и будет
вектор
будет
вектор .
Итак
.
Итак .
.



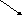

Суммой векторов
 называется третий вектор
называется третий вектор ,
начало которого совпадает с началом
вектора
,
начало которого совпадает с началом
вектора ,
а конец – с началом вектора
,
а конец – с началом вектора ,
отложен из конца вектора
,
отложен из конца вектора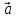 .
.
Правило
параллелограмма: если даны два
неколлинеарных вектора
 ,
то откладываем их от одной произвольным
образом выбранной точки А пространства
,
то откладываем их от одной произвольным
образом выбранной точки А пространства .
Затем строим на отрезках АВ иAD
параллелограмм ABCD.
Вектор
.
Затем строим на отрезках АВ иAD
параллелограмм ABCD.
Вектор







Естественно, что
сумма
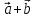 векторов
векторов ,
найденная по правилу параллелограмма
не зависит от выбора точки А и совпадает
с суммой
,
найденная по правилу параллелограмма
не зависит от выбора точки А и совпадает
с суммой векторов
векторов ,
найденной по правилу треугольника.
,
найденной по правилу треугольника.
Правило
параллелепипеда: если даны три
некомпланарных вектора
 ,
то откладываем их от одной произвольным
образом выбранной точки А пространства
,
то откладываем их от одной произвольным
образом выбранной точки А пространства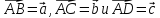 .
Затем строим на отрезках АВ, АС иAD,
как на рёбрах, параллелепипед. Вектор
.
Затем строим на отрезках АВ, АС иAD,
как на рёбрах, параллелепипед. Вектор
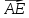 ,
где
,
где – диагональ на рёбрах параллелепипеда,
есть сумма
– диагональ на рёбрах параллелепипеда,
есть сумма векторов
векторов ,
то есть.
,
то есть.




Вычитание векторов.
Вычесть из вектора
 вектор
вектор –
значит найти такой вектор
–
значит найти такой вектор ,
который в сумме с вектором
,
который в сумме с вектором даст вектор
даст вектор .
если из вектора
.
если из вектора ,вычитается
вектор
,вычитается
вектор ,
то будем писать
,
то будем писать .
Вектор
.
Вектор будем называть разнице векторов
будем называть разнице векторов .
Итак,
.
Итак, двух векторов
двух векторов ,
необходимо их одной произвольным образом
выбранной точки А пространства отложить
векторы
,
необходимо их одной произвольным образом
выбранной точки А пространства отложить
векторы .
затем конец С вектора
.
затем конец С вектора соединить с концом В вектора
соединить с концом В вектора .
Получим вектор
.
Получим вектор ,
который и будет разностью
,
который и будет разностью векторов
векторов .
.




Умножение вектора на число.
Пусть дан вектор
 и действительное числоβ≠0
и действительное числоβ≠0
Произведением
вектора
 на
числоβ≠0
называется вектор
на
числоβ≠0
называется вектор
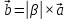 такой,
что
такой,
что
Модуль

Вектор
 сонаправлен
с вектором
сонаправлен
с вектором ,
если числоβ
>0; вектор
,
если числоβ
>0; вектор
 направлен противоположно вектору
направлен противоположно вектору ,
если числоβ<
0.
,
если числоβ<
0.
Если
 илиβ = 0, то
полагаем, что β×
илиβ = 0, то
полагаем, что β× =
= и 0×
и 0× =
=





35. Скалярное произведение векторов
 ,
,
 ортогонален
ортогонален (
( )
) .
Длины
.
Длины
 ;
; .
.
Угол
между векторами

36.
Векторным
произведением векторовa
и b
называется вектор c
, который определяется следующими
условиями:1) Его модуль равен a*b*sin![]() где
где
![]() - угол между векторами .
- угол между векторами .
2) Вектор cперпенд к плоскости, опр-мой перемнож векторами a и b .
3) Вектор c направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы a и b, кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать противчасовой стрелки (см. рисунок).

Основные свойства векторного произведения
1) Векторное произведение a*b=0 , если векторы a и bколлинеарны или какой-либо из перемножаемых векторов является нулевым.
2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный вектора a*b=-b*a .Векторное произведение не обладает свойством переместительности.