
- •4. Полярная система координат на плоскости.
- •5. Прямоугольные декартовые координаты пространств.
- •9. Угол между двумя прямыми. Расстояние от точки до прямой.
- •10. Линии второго порядка. Окружность.
- •11.Линии второго порядка.Эллипс
- •12. Линии второго порядка.Гипербола.
- •13 Линии второго порядка. Парабола
- •14 .Основные понятия и определения. Теория матрицы
- •15. Линейные действия над матрицами
- •16.Произведение матриц
- •17.Транспонировние матрицы
- •18. Определители 2-ого и 3-ого порядков.
- •19. Обратная матрица
- •20. Ранг матрицы
- •21. Система линейных уравнений. Основные понятия
- •22.Решение систем линейных уравнений с помощью определителя(теорема Крамера)
- •23. Исследование систем линейных уравнений (теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)
- •24.Матричный метод решения систем линейных уравнений
- •25)Метод Гаусса решения систем линейных уравнений.
- •29.Умножение вектора на число. Свойства линейных операций над векторами.
- •31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
- •Вопрос32. Разложение вектора по базису
- •Вопрос33.Прямоугольные декартовы координаты в пространстве
- •34. Длина вектора. Линейные операции над векторами в прямоугольных координатах: сумма, разность, умножение на число. Признак коллинеарности двух векторов в прямоугольных координатах.
- •35. Скалярное произведение векторов
- •37.Смешанное произведение 3 векторов.
- •38. Линейная зависимость векторов
- •39.Уравнение поверхности и линии
- •Уравнение плоскости, проходящей через три точки
- •41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки
- •44. Понятие сложной функции. Четные и нечетные функции, переодические функции.Основные элементарные функции.
- •45. Функция натурального аргументы и ее предел.
- •47. Предел функции в точке и на бескон. Определение
- •49. Основныесв-ва пределов функций.
- •50.Замечательные пределы
- •51. Непрерывные ф-ции.Точки разрыва ,их классификация.
29.Умножение вектора на число. Свойства линейных операций над векторами.
Произведением
ненулевого вектора ![]() на
действительное число
на
действительное число![]() называется
вектор
называется
вектор![]() ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
1) длина
вектора ![]() равна
равна![]() ,
т.е.
,
т.е.![]() ;
;
2)
векторы ![]() и
и![]() коллинеарные
коллинеарные![]() ;
;
3)
векторы ![]() и
и![]() одинаково
направлены, если
одинаково
направлены, если![]() ,
и противоположно направлены, если
,
и противоположно направлены, если![]() .
(рис. 9). Если среди сомножителей
.
(рис. 9). Если среди сомножителей
 есть 0, то под произведением
есть 0, то под произведением понимается нулевой вектор.
понимается нулевой вектор.
Геометрический
смысл операции умножения вектора на
число следующий: если
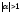 ,
то при умножении вектора
,
то при умножении вектора на число
на число вектор
вектор «растягивается» в
«растягивается» в раз, а если
раз, а если – «сжимается» в
– «сжимается» в раз. На рис. 9 изображен случай
раз. На рис. 9 изображен случай .
.
Утверждение
1. Если
векторы
 и
и коллинеарны
и
коллинеарны
и ,
то существует единственное число
,
то существует единственное число ,
что
,
что .
.
Свойства линейных операций над векторами
Сложение
векторов и умножение вектора на число
называются линейными
операциями над векторами.
Для любых векторов ![]() ,
,![]() ,
,![]() и
любых действительных чисел
и
любых действительных чисел![]() справедливы
равенства:
справедливы
равенства:

30.Угол между векторами. Скалярное произведение векторов

Скалярным
произведением двух
ненулевых векторов ![]() и
и ![]() называется
число, равное произведению длин этих
векторов на косинус угла между ними:
называется
число, равное произведению длин этих
векторов на косинус угла между ними:
![]()

31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
Проведём
a
и b, ,
,
 ,a
,a b,
b,
 .
Из точки О
отложим
.
Из точки О
отложим
 .По
правилу парал. сложения векторов устанав,
что
.По
правилу парал. сложения векторов устанав,
что ,
где
,
где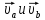 сост
вектора
сост
вектора
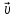 ,
леж на прямыхa
и b,
соответственно. Предст вектора
,
леж на прямыхa
и b,
соответственно. Предст вектора равенством назразлож
вектора
равенством назразлож
вектора
 на
состав
на
состав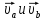 ,
леж на прямых a
и b.Заданы
прямая
,
леж на прямых a
и b.Заданы
прямая
 и плоскость
и плоскость
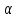 ,
причём
,
причём не лежит в
не лежит в и не паралл
и не паралл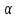 .
. .
.


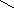
Возьмём
 и отложим его от О. Получим
и отложим его от О. Получим .
Пусть точка
.
Пусть точка – проекцияV
на
– проекцияV
на
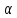 в направлении в направлении
в направлении в направлении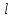 ,
то есть
,
то есть .
. на
на выбрана так, что
выбрана так, что
Тогда (1)
(1)
или (2),где
(2),где явл сост
явл сост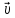 ,
леж на
,
леж на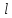 и на
и на .Представление
.Представление равенствами(1) или(2) назывразлож
равенствами(1) или(2) назывразлож на
составл
на
составл ,
леж на
,
леж на
 и на
и на .Пусть
заданы три прямые a,
b,
c,
пересек в O
и не леж в одной плоскости.
.Пусть
заданы три прямые a,
b,
c,
пересек в O
и не леж в одной плоскости.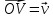 .
Разлаживаем
.
Разлаживаем
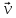 по прямa
и плосa:
по прямa
и плосa:

на
составляющие
 Теперь
Теперь
 разложим на составляющие
разложим на составляющие
 , леж наb
и c,
в a
:
, леж наb
и c,
в a
: В
итоге имеем, что
В
итоге имеем, что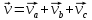 .где
.где
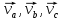 составляющиеv,леж
на a,
b,
c,соответственно.Представление
составляющиеv,леж
на a,
b,
c,соответственно.Представление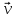 назыв разлож
назыв разлож
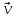 на сост
на сост ,
леж наa,
b,
c.
,
леж наa,
b,
c.
Вопрос32. Разложение вектора по базису
Разложить
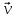 по базису
по базису
 – это значит представить его
– это значит представить его .Числкоэфx,
y,
zв
правой части равенства – координаты
.Числкоэфx,
y,
zв
правой части равенства – координаты
 в базисе
в базисе
 .Координаты
векторов (как и их сост.) обладают
след.св-ми (операции слож. векторов и
умн. на число):
При
слож векторов их координаты
складываются.
Разл.
вектора
.Координаты
векторов (как и их сост.) обладают
след.св-ми (операции слож. векторов и
умн. на число):
При
слож векторов их координаты
складываются.
Разл.
вектора
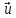 по базису
по базису имеет вид
имеет вид
 ,
где
,
где
 – действ.числа. Тогда сум.
– действ.числа. Тогда сум. ,
и предст. вектор
,
и предст. вектор с координатами
с координатами ,
, ,
,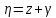 в базисе
в базисе
При
умнож.вектора на число его координаты
умнож. на это число. - действ. число. Разлож
- действ. число. Разлож по базису
по базису
 имеет вид
имеет вид .
Тогда
.
Тогда .Тройка
базисных векторов в пространстве наз.
Правой (левой), если эти векторы, отлож.
от одной точки, распол. так, как распол.
большой, указательный и средний пальцы
правой (левой) руки.
.Тройка
базисных векторов в пространстве наз.
Правой (левой), если эти векторы, отлож.
от одной точки, распол. так, как распол.
большой, указательный и средний пальцы
правой (левой) руки.
Вопрос33.Прямоугольные декартовы координаты в пространстве
Координатами
вектора
 ,
начало кот. Точка А(
,
начало кот. Точка А( ),
а конец В(
),
а конец В( )
в прям. дек. системе координатOxyz
наз. числа
)
в прям. дек. системе координатOxyz
наз. числа
 ,
, ,
, . Сначала фикс. в прям. дек. сист. координат
Охуz
точку А(х, у, z).
Потом строят точку В(х+
. Сначала фикс. в прям. дек. сист. координат
Охуz
точку А(х, у, z).
Потом строят точку В(х+ ,
у+
,
у+ ,
z+
,
z+ ).
Получаем
).
Получаем равн.
равн. .
Радиусом-вектором – наз. вектор
.
Радиусом-вектором – наз. вектор с точкой прилож. в нач. координат О, а
конец - в А.
с точкой прилож. в нач. координат О, а
конец - в А. .
.
