
- •4. Полярная система координат на плоскости.
- •5. Прямоугольные декартовые координаты пространств.
- •9. Угол между двумя прямыми. Расстояние от точки до прямой.
- •10. Линии второго порядка. Окружность.
- •11.Линии второго порядка.Эллипс
- •12. Линии второго порядка.Гипербола.
- •13 Линии второго порядка. Парабола
- •14 .Основные понятия и определения. Теория матрицы
- •15. Линейные действия над матрицами
- •16.Произведение матриц
- •17.Транспонировние матрицы
- •18. Определители 2-ого и 3-ого порядков.
- •19. Обратная матрица
- •20. Ранг матрицы
- •21. Система линейных уравнений. Основные понятия
- •22.Решение систем линейных уравнений с помощью определителя(теорема Крамера)
- •23. Исследование систем линейных уравнений (теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)
- •24.Матричный метод решения систем линейных уравнений
- •25)Метод Гаусса решения систем линейных уравнений.
- •29.Умножение вектора на число. Свойства линейных операций над векторами.
- •31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
- •Вопрос32. Разложение вектора по базису
- •Вопрос33.Прямоугольные декартовы координаты в пространстве
- •34. Длина вектора. Линейные операции над векторами в прямоугольных координатах: сумма, разность, умножение на число. Признак коллинеарности двух векторов в прямоугольных координатах.
- •35. Скалярное произведение векторов
- •37.Смешанное произведение 3 векторов.
- •38. Линейная зависимость векторов
- •39.Уравнение поверхности и линии
- •Уравнение плоскости, проходящей через три точки
- •41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки
- •44. Понятие сложной функции. Четные и нечетные функции, переодические функции.Основные элементарные функции.
- •45. Функция натурального аргументы и ее предел.
- •47. Предел функции в точке и на бескон. Определение
- •49. Основныесв-ва пределов функций.
- •50.Замечательные пределы
- •51. Непрерывные ф-ции.Точки разрыва ,их классификация.
15. Линейные действия над матрицами
Линейные действия наматрицами – сложение и вычитание матриц, умножение матриц на число. Сложение и вычитание матриц определяется только для матриц одинаковой размерности.
Суммой(разностью)
матриц А и В
одинаковой размерности m*n
называется матрица С, элементы которой
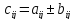 (
(
Произведение
матрицы А на число
 называется матрица αА, полученный из
данной матрицы А умножением всех
ее
элементов на число α
называется матрица αА, полученный из
данной матрицы А умножением всех
ее
элементов на число α
Матрицу (-1)А называют противоположной матрице А и обозначают –А
Свойства линейных операций над матрицами
А+В=В+А
(А+В)+С=А+(В+С)
А+0=А
А+(-А)=0
1(А)=А
α(βА)=(αβ)А
α(А+В)=αА+αВ
(α+β)А=αА+βА
16.Произведение матриц
Произведением
матрицы А=(аij),(m×n)
на матрицу В(bij),(n×k)называется
матрица C=(cij),(n×k)
у которой каждый элемент( Cij)вычисляется
по формуле Cij=aij*bij+ai2*b2j+…+ain*bnj= ailblj,
i=1,m,
j=1,n
ailblj,
i=1,m,
j=1,n
Произведение матрицы А на матрицу В обозначают АВ
Умножение матрицы А на матрицу В можно лишь тогда, когда число столбцов матрицы А= числу строк матрицы В
Свойства умножения матриц:
(АВ)*С = А*(ВС)
Α*(АВ)=(αА)В=А(αВ)
(А+В)*С=АС+ВС
С*(А+В)=СА+СВ
А*Е=Е*А=А
А*0=0*А=0
17.Транспонировние матрицы
Матрица
полученная из данной матрицы заменой
каждой её строки столбцом с тем же
номером называется транспонированной
относительно данной обозначают: АТ,
так по определению транспонированная
матрица к матрице A=(
 )
имеет вид АТ=
)
имеет вид АТ=
Свойства операции транспонирования:
(АТ)Т=А
(А+В)Т=АТ+ВТ
(α*А)Т=α*АТ
(АВ)Т=ВТ*АТ
18. Определители 2-ого и 3-ого порядков.
Определителем
квадратной матрицы 2-ого порядка А= );
(1)
);
(1)
а11* а22 – а21*а12
Определитель
называют так же детерминантом, обозначают:
lAl,
∆,
detA,
det(aij)
значит по определению: lAl=
 =
=
Элементы, строки, столбцы, диагонали и порядок матриц называют соответственно элементами, строками, столбцами, диагоналями и порядками.
Определителем
квадратной матрицы 3-ого порядка
 ;(2)
называется числоlAl=
;(2)
называется числоlAl=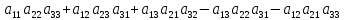 (3) .
(3) .
заметим
что каждое слагаемое алгебраической
суммы(3) представляет собой произведение
элементов определителя взятых по одному
и только по одному из каждой строки и
каждого столбца. Этому произведению
приписывается соответственный знак
для запоминания которого используют
схему.
Минором
какого-либо элемента определителя
называют определитель полученный из
данного определителя вычёркиванием
строки и столбца которым принадлежит
данный элемент. Минор элемент
 ,
обозначают
,
обозначают .
Минором определителя 3-ого порядка
является определитель 2-ого порядка.
.
Минором определителя 3-ого порядка
является определитель 2-ого порядка.
Алгебраическим
дополнением элемента определителя называют его минором
взятый со знаком
определителя называют его минором
взятый со знаком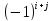

Свойство определителей:
Определитель не изменится при заме всех его соответствующим столбцам,т.е. detA = detAT
При перестановке 2 строк(столбцов) определитель меняет знак
Определитель с двумя одинаковыми строками (столбцами) равен 0
Множитель общий для некоторой строки (столбца) можно выносить за знак определителя
Определитель равен 0, если все элементы некоторой строки (столбца) равен 0
Определитель не изменится если к элементам некоторой строки (столбца) прибавить соответственные элементы другой строки (столбца) предварительно умножив их на один и тот же множитель
Теорема Лапласа: определитель равен сумме произведения элементов любой строки (столбца) на их алгебраические дополнения.
 =
=
 , где
, где j–пробегает
всё множество j=1,n
j–пробегает
всё множество j=1,n
Определитель равен 0 если элементы некоторых двух строк (столбцов) пропорциональны
Если элементы некоторой строки (столбца) представляет собой сумму двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых соответствует строка (столбец) состоит из первых слагаемых, а во втором из вторых слагаемых.
