47. Предел функции в точке и на бескон. Определение

1) Число Аназыв. Пределом функции у=f(x), в точке Xo, если для любой последоват.(Хn) принадлежащие D(y), n принадлежит Nимеющ.в своих пределах точку Хо, то есть предел числа Хn и стремящееся к бесконечности равно Хo, последоват.(f(Xn)) имеет в своих пределах большое число A, то есть . Еслии А- дейсвит.число, то говорят, что в точке Хо функция у=f(x) имеет конечный предел равный А. Пусть функция у=f(x) определена в нек. ε-окрестности точки Хо, за исключением Хо. Сформулируем определ. предела ф-ции в терминах окрестности и называемым определение предела ф-ции по Коши. Определение 2 Число А-предел функции у=f(x) в точке Хо (при x→x₀), где x₀R, если для любого ε˃0 сущ. δ=δ(ε)˃0, для всех x, ˂δ→˂ε,

Геометрический 8предел А функции у=f(x) при Х стремящейся к Хо означает, что какую бы горизонтальную Е полосу мы не взяли симметричную вдоль прамой у=А, всегда найдется дельта полоса симметричная прямой Х=Хо, такая что все точки графика функции расположенные в вертикальной полосе, кроме точки наход.на прямой Х=Хо обязательно попадет в горизонтальную полосу. При изучении ф-ций иногда оказывается полезным рассмотреть пределы на мн-вах являющихся частями множеств определенияф-ций и лежащими по одну сторону от точки в кот.рассм. предел. Такие пределы назыв. односторонними. Это понятие содержательно лишь тогда, когда x₀R. . Односторонние пределы. В определении предела функции считается, чтох стремится к а любым способом: оставаясь меньше, чем а (слева от а) или больше, чем а (справа от а).

Бывают случаи, когда способ приближения аргумента хка существенно влияет на значение предела функции. Поэтому вводят понятие односторонних пределов.

Число b называется правым пределом (пределом справа) в точке , если для любой сходящейся ка последовательности , члены которой больше или равныа (), соответствующая последовательностьсходится кb; обозначается: .

Аналогично, число b называется левым пределом (слева) в точке , если,, соответствующая последовательностьсходится кb; обозначается: .

Естественно, что можно сформулировать эти определения «на языке ».

Правый и левый пределы функций в точке называются односторонними. В случае, когда , используются обозначения:,.

Коротко предел слева и справа обозначают .

Очевидно, если существует 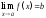, то существуют и оба односторонних предела, причемсовпадает с ними. Справедливо и обратное утверждение: если существуют оба предела,, и они равны, то существует предели.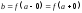

Если же  , то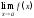не существует.

48. БМ и ББ фу-ции. Определение и основные свойства.Функция 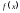называетсябесконечно малойпр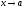и, если.Функцияназываетсябесконечно большой при , если.Например, функцияесть бесконечно большая функция при.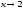

Имеет место следующее утверждение, характеризующее связь между б. м. функциями б.б функциями.

Утверждение 1. Для того, чтобы функция прибыла б.м.функцией, необходимо и достаточно, чтобы функциябылаб. б. функцией при .

Для б. м. функции выполняются те же свойства, что и для б. м.последовательностей.

Пример 1. Показать, что функция прих  1 является б. м.

Решение. Т.к. , то функцияестьб. м.прих  1. Функция ,х  1, ограничена: . Функцияпредставляет собой произведение ограниченной функции наб. м.. Значит –б. м. при х  1 Основные св-ва пределов функций.

₁.если ф-я f(х) имеет в т.x_{0,то он единственный}

_{2.если ф-я f(х)імеет в т. x0предел,то сущ. окресность в т. х0,в кот. Ф-я f(х) ограничена}

_{3.если у=С-пост. Ф-я,то}

_{4.если,,то а)lim(f±g)=A+B; б)(f*g)=A*B; в)f/g=A/B, B≠0}

_{5.если в окрестности в т. х0 выполняются нер-ваf1(x)≤f(x)≤f2(x) и} , то и

_{6.сохранение знака предела. Если ,то сущ. окрестность в т.x0 такая, что f(х)>0 (f(x) <0)при всех х из этой окрестности.}