
- •4. Полярная система координат на плоскости.
- •5. Прямоугольные декартовые координаты пространств.
- •9. Угол между двумя прямыми. Расстояние от точки до прямой.
- •10. Линии второго порядка. Окружность.
- •11.Линии второго порядка.Эллипс
- •12. Линии второго порядка.Гипербола.
- •13 Линии второго порядка. Парабола
- •14 .Основные понятия и определения. Теория матрицы
- •15. Линейные действия над матрицами
- •16.Произведение матриц
- •17.Транспонировние матрицы
- •18. Определители 2-ого и 3-ого порядков.
- •19. Обратная матрица
- •20. Ранг матрицы
- •21. Система линейных уравнений. Основные понятия
- •22.Решение систем линейных уравнений с помощью определителя(теорема Крамера)
- •23. Исследование систем линейных уравнений (теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)
- •24.Матричный метод решения систем линейных уравнений
- •25)Метод Гаусса решения систем линейных уравнений.
- •29.Умножение вектора на число. Свойства линейных операций над векторами.
- •31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
- •Вопрос32. Разложение вектора по базису
- •Вопрос33.Прямоугольные декартовы координаты в пространстве
- •34. Длина вектора. Линейные операции над векторами в прямоугольных координатах: сумма, разность, умножение на число. Признак коллинеарности двух векторов в прямоугольных координатах.
- •35. Скалярное произведение векторов
- •37.Смешанное произведение 3 векторов.
- •38. Линейная зависимость векторов
- •39.Уравнение поверхности и линии
- •Уравнение плоскости, проходящей через три точки
- •41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки
- •44. Понятие сложной функции. Четные и нечетные функции, переодические функции.Основные элементарные функции.
- •45. Функция натурального аргументы и ее предел.
- •47. Предел функции в точке и на бескон. Определение
- •49. Основныесв-ва пределов функций.
- •50.Замечательные пределы
- •51. Непрерывные ф-ции.Точки разрыва ,их классификация.
Уравнение плоскости, проходящей через три точки
Даны три точки
![]() ,
,
не
лежащие на одной прямой. Требуется
написать уравнение плоскости, проходящей
через эти три точки. Из геометрии
известно, что такая плоскость существует
и единственная. Так как она проходит
через точку ![]() ,
то ее уравнение имеет вид
,
то ее уравнение имеет вид
![]() ,
(9)
,
(9)
где ![]() ,
, ![]() ,
, ![]() одновременно
не равны нулю. Так как она проходит еще
через точки
одновременно
не равны нулю. Так как она проходит еще
через точки ![]() ,
, ![]() ,
то должны выполняться условия:
,
то должны выполняться условия:
 (10)
(10)
Составим
однородную линейную систему уравнений
относительно неизвестных ![]() ,
, ![]() ,
, ![]() :
:
 (11)
(11)
Здесь ![]() есть
произвольная точка, удовлетворяющая
уравнению плоскости (9). В силу (9) и (10)
системе (11) удовлетворяет нетривиальный
вектор
есть
произвольная точка, удовлетворяющая
уравнению плоскости (9). В силу (9) и (10)
системе (11) удовлетворяет нетривиальный
вектор ![]() ,
поэтому определитель этой системы равен
нулю
,
поэтому определитель этой системы равен
нулю
 .
.
Мы
получили уравнение вида (9), т. е. уравнение
плоскости, в чем легко убедиться, разложив
полученный определитель по элементам
первой строки. При этом эта плоскость
проходит через точки ![]() ,
, ![]() ,
, ![]() ,
что вытекает из свойств определителя.
Наша задача решена.
,
что вытекает из свойств определителя.
Наша задача решена.
Уравнение (12) можно еще написать и в следующем виде:
 .
(13)
.
(13)
Если из первой, третьей и четвертой строк определителя в (13) вычесть вторую строку, то он не изменится. Разлагая результат по элементам четвертого столбца, получим уравнение (12).
Уравнение
плоскости, проходящей через две точки
и параллельной данному вектору.
Если задан вектор![]() И
две точки
И
две точки![]()

![]() Причем
векторы
Причем
векторы![]() И
И![]() .
неколлицеарны (рис. 4.6), то уравне-
.
неколлицеарны (рис. 4.6), то уравне-
Ние плоскости, проходящей через эту точку параллельно вектору а, имеет вид
(4-15)

Равенство
(4.15) выражает необходимое и достаточное,
условие компланарности трех
 векторов
векторов![]()
![]() -
любая точка данной rmoikOtm
-
любая точка данной rmoikOtm
Уравнение
плоскости, проходящей через данную
точку и параллельной двум неколлннеарным
векторам. Были
даны два неколлинеарных вектора (рис.
4.7)![]() И
точка
И
точка![]() :
то уравнение плос
:
то уравнение плос
Кости, проходящей через данную точку параллельно векторам а и Ь, имеет вид

(4.16)
Равенство
(4.16) выражает необходимое и достаточное
условие компланарности трех векторов:![]() Где
Где![]() -
произвольная точка данной плоскости.
-
произвольная точка данной плоскости.
41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки
Направляющим вектором прямой называется любой не нулевой вектор параллельный этой прямой.
Каноническое
уравнение прямой в пространстве,
проходящей через M0
(x0y0
z0)
и имеющий направленный вектор а (а1
а2
а3)
х-х0= y-y0 = z-z0 (1)
а1 a2 a3
Прямую линию в пространстве можно задать еще как результат пересечения плоскостей, т.е. систему уравнений

Если каждую из дробей равенства (1), обозначить через t, то путем алгебраических преобразований перейдем к параметрическому заданному уравнению прямой
x= x0 +a1t, y= y0+a2t, z=z0+a3t (2)
Если
даны 2 точки М1
(x1y1z1)
и М2(x2y2z2),
то в качестве направляющего вектора,
можно взять вектор 
М1М2 = (x2-x1, y2-y1, z2-z1)
Поэтому равенство (1) примет вид
 =
=
 =
=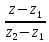 (3)
(3)
Которое называется уравнение прямой, проходящей через 2 точки.
43.Постоянные и переменные величины.Функциональнаязависимость.Понятие функции и основные способы ее задания. Переменные величины — это такие величины, которые в условиях данного вопроса могут принимать различные значения. Постоянные величины — это такие величины, которые в условиях данного вопроса сохраняют неизменные значения.2) Функциональной зависимостью называется связь между двумя величинами, при которой изменение одной из них вызывает изменение другой.3)Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменнаяТабличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Преимущества табличного способа ~он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений.. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнениемАналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
