37.Смешанное произведение 3 векторов.

Смешанным произведением 3 векторов называется скалярное произведение векторов,и обозначается.

Смешанное произведение,равноVпараллелепипеда, построенного на этих векторах.

Свойства смешанных произведений.

1. 0, если: хотя бы один=0; 2 из векторов коллинеарные(параллельны); все 3 вектора компланарны (параллельны одной и той же плоскости или лежат в одной плоскости)

2. Смешанное произведение не изменится, если в нем знак векторного х и скалярного *,поменять местами.(+)*=(

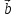3. При перестановке 2 векторов, смешанное произведение меняет знак

Из свойств 1-4 и определения смеш.произведения следует, что

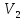(пирамид,построенных на abc) ==

V(пирамиды)=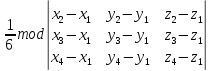

(М(x,y,z))1,4)

38. Линейная зависимость векторов

Векторы –линейно зависимы, если существуют действительные числа , среди которых есть числа отличные от 0 действительные числа, что выполняют равенство

(1)

Если равенство (1) выполняется при , то векторы –линейно зависимы.

Справедливы утверждения:

1. Векторы , лин. Зависимы тогда и только тогда, когда по меньшей мере один из них явл. Линейной комбинацией других.

2. 2 вектора линейно зависимы тогда и только тогда, если они коллинеарные .

3. Если – 2 коллинеарные вектора в одной плоскости, то любой 3 вектор,этой плоскости можно разложить по ним:a= x* .

4. 3 векторалин.зависимы тогда и только тогда, когда они компланарны.

5. Любой можно разложить по 3 некомпланарным векторам:

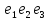6. Всякие 4 вектора пространства зависимы.

39.Уравнение поверхности и линии

Уравнение поверхности фиксированной системы OXYZ, называется такое уравнение F(x,y,z)=0, где F-функция переменных x,y,z,которому удовлетворяет координаты любой точки поверхности и только они.

При составлении уравнения поверхности, придерживаются следующего плана:

1. В выбранной системе координат OXY берут произвольную точку М, считая, что она принадлежит рассматр. поверхности (эту точку называют текущей, а ее координаты текущими).

2. Составляем соотношение между текущими координатами, которые определяют данные поля(шар).

Линию в пространстве можно рассматривать как пересечение 2 поверхностей.

Пусть F(x,y,z)=0 Ф(x,y,z)=0-ур-е поверхности , пересекающейся по данной линии е, тогда координаты любой точки линии е , удовлетворяют системе

Иногда рассматриваем е,для описания траектории движения точки с течением времени t.

Ур-е линии x=x(t)

y=y(t)

z=z(t), где x,y,z-функции времени.

40. Различные виды уравнения плоскости (частные виды уравнения плоскости; Уравнение плоскости, проходящей через данную точку перпендикулярно нормальному вектору; уравнение плоскости в отрезках; уравнение плоскости, проходящей через три данные точки; Уравнение плоскости, проходящей через две данные точки и параллельные данному вектору; Уравнение плоскости, проходящей через данную точку и параллельной двумнеколлинеарным векторам)

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:

Составить уравнение плоскости, проходящей через данную точку

M(x0,y0,z0) перпендикулярно данному вектору →n= {A,B,C} .

Решение. Пусть P(x,y,z) — произвольная точка пространства. ТочкаPпринадлежит плоскости тогда и только тогда, когда вектор

MP= {x−x0,y−y0,z−z0} ортогонален вектору →n= {A,B,C} (рис.1).

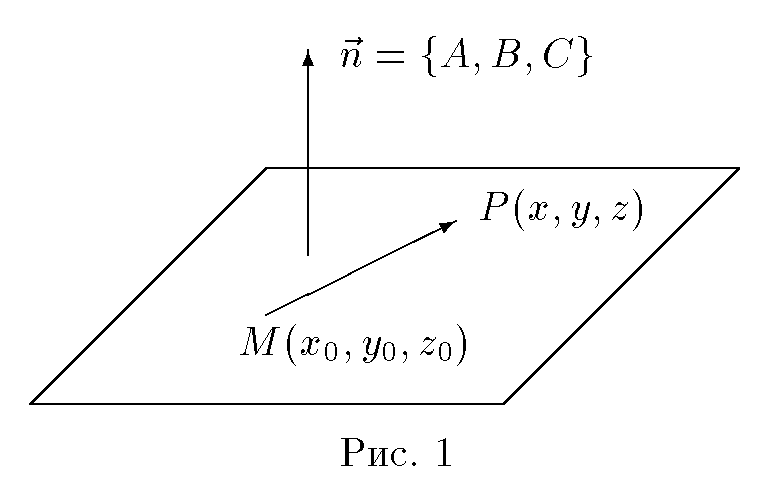
Написав условие ортогональности этих векторов ( → n,MP) = 0 в координатной форме, получим:

A(x−x0) +B(y−y0) +C(z−z0) = 0 (1)

Это и есть искомое уравнение. Вектор → n= {A,B,C} называется нормальным вектором плоскости.

Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости.

Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:

Ax + By + Cz + D = 0 ,

где D = −Ax0 − By0 − Cz0 .

Уравнение плоскости в отрезках.

Уравнение плоскости вида , гдеa, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках.

Такое название не случайно. Абсолютные величины чисел a, b и c равны длинам отрезков, которые отсекает плоскость на координатных осях Ox, Oy и Oz соответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) следует откладывать отрезки на координатных осях.

Для примера построим в прямоугольной системе координат Oxyz плоскость, определенную уравнением плоскости в отрезках . Для этого отмечаем точку, удаленную на5 единиц от начала координат в отрицательном направлении оси абсцисс, на 4 единицы в отрицательном направлении оси ординат и на 4 единицы в положительном направлении оси аппликат. Осталось соединить эти точки прямыми линиями. Плоскость полученного треугольника и есть плоскость, соответствующая уравнению плоскости в отрезках вида .