Метрологические основы аналитической химии.

Пример 1. Определите доверительный интервал среднего арифметического для выборки результатов, полученных при определении содержания массы Na₂CO₃ в 100 мл раствора соды прямым титрованием его аликвотных частей раствором соляной кистоты в граммах: 0,2031; 0,2033; 0,2015; 0,2048; 0,2020, где число вариант n=5, среднее арифметическое Х=0,2029г, а стандартное отклонение выборки S=0.0013г.

Решение. При вероятности Р=0,95 по табл.1 определяют коэффициент Стьюдента: в данном случае при n=5,t=2.776.

По формуле находят точность погрешности среднего арифметического выборки:

2.776·0.0013/√5=0.001614.

Поскольку точность погрешности среднего арифметического не может быть выше точности самой величины , после округления получают

Следовательно, доверительный интервал составляет

0,2029±0,0016 или 0,2013<<0,2045 для Р=95%.

Таблица 1

Коэффициенты Стьюдента t

Число вариант n	Число степеней свободы f=n-1	Значения t при Р
		0,90 0,95 0,99
2	1	6,314	12,71	65,66
3	2	2,920	4,303	9,925
4	3	2,353	3,182	5,841
5	4	2,132	2,776	4,604
6	5	2,015	2,571	4,034
7	6	1,94	2,45	3,71
8	7	1,90	2,37	3,5
9	8	1,86	2,31	3,36
10	9	1,83	2,26	3,25
11	10	1,81	2,23	3,17
16	15	1,75	2,13	2,95
21	20	1,73	2,09	2,85

Пример 2 . Оцените наличие промахов в выборке результатов, приведенных в примере 1.

Решение. Располагают результаты выборки в порядке их возрастания и определяют диапазон выборки:

0,2015; 0,2020; 0,2031; 0,2033; 0,2048;

w=0.2048-0.2015=0.0033.

Поскольку в данной выборке n>3, проверяем на промах наибольшую варианту по уравнению:

Q_p=(X_i+1 –X_i)/w , Q_p- расчетная величина критерия; X_i+1-подвергаемое сомнению значение; X_i- соседнее с ним значение выборки; w-диапазон выборки.

Q_p=(0,2048-0,2033)/0,0033=0,45.

По таблице 2 при Р=0,95 в случае n=5 Q_t=0.73

Так как 0,45<0,73 или Q_p< Q_t ,то проверяемое значение не является промахом. Следовательно, промахи в данной выборке отсутствуют.

Таблица 2

Табличные коэффициенты Q_t

Число вариант n	Значение Qt при Р
	0,90	0,95	0,99
3	0,94	0,98	0,99
4	0,76	0,85	0,93
5	0,64	0,73	0,82
6	0,56	0,64	0,74
7	0,51	0,59	0,68
8	0,47	0,54	0,63
9	0,44	0,51	0,60
10	0,41	0,48	0,57

Пример 3. При кислотно-основном титровании аликвотных частей того же раствора соды, что и в примере 1, но выполненном с применением нового индикатора, была получена выборка результатов (в граммах): 0,2030; 0,2038; 0,2039; 0,2050. Оцените статистическую однородность стандартных отклонений обеих выборок и их средних арифметических значений, если применение Q-теста ко вновь полученной выборке показало, что промахи в ней отсутствуют, а рассчитанные ее метрологические характеристики следующие: 2=0,2039; S₂²=67.7·10^-8.

Решение. 1.Сравнив значения дисперсий рассматриваемых выборок, определяют расчетное значение F-критерия:

Первая выборка результатов : n₁=5; X₁=0.2029; S₁²=164.5·10^-8.

Вторая выборка: n₂=4; ₁=0.2029; S₂²=67.7·10^-8.

Так как S₁²> S₂², в числитель уравнения F_p= S₁²/ S₂²,( S₁²-большая по значению дисперсия) F-критерия следует поместить значение дисперсии первой выборки результатов:

F_p=164,5·10^-8/(67,7·10^-8)=2,43.

По таблице 3 с учетом n₁=5, a n₂=4(соответственно f₁=4, f₂=3) для Р=0,95 определяют теоретическое значение F-критерия: F_т=9,12.

Поскольку 2,43<9,12 или F_p< F_т, расхождение между дисперсиями данных выборок незначительно, следовательно, обе выборки равнозначны.

Определяем средневзвешенную дисперсию по уравнению

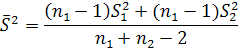
(где индекс 1 относится к числу вариант (n) и дисперсии (S) первой вборки, индекс 2- соответственно ко второй.)

Рассчитаем t-критерий по уравнению

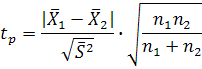
где -- расчетная величина t-критерия; n₁ n₂—число вариант выборки соответственно с дисперсией S₁² S₂².

=

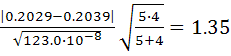
По таблице 1 для Р=0,95 и f=5+4-2=7 находим t_т=2,37.

Так как 1,35<2,37 или t_p<t_т, следовательно, значимого различия между рассматриваемыми величинами средних арифметических значений не существует. Таким образом, применение нового индикатора не приводит к систематическим погрешностям при титровании, т.е. к изменению точности результатов.

Задачи для самостоятельного решения.

1.При определении содержания свинца в сплаве были получены следующие результаты (%): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,25; 14,19. Оцените наличие промахов, рассчитайте среднее арифметическое и доверительный интервал.

2.Определите, является ли последний результат промахом:

а)При анализе получены следующие данные о содержании в топазе Al₂O₃(%): 53,96; 54,15; 54,05; 54,08; 54,32.

б)При анализе получены данные о содержании в апатите Р₂О₅(%):

35,11; 35,14; 35,18; 35,21; 35,42.

в)При определении гравиметрическим методом сульфат-иона получены следующие данные о содержании SO₃(%):15,51; 15,45; 15,48; 15,53; 16,21.

3.Вычислите стандартное отклонение единичного определения и доверительный интервал среднего значения для Р=0,95:

а) При определении ванадия получены следующие результаты (в граммах):

8,00·10^-4; 8,40·10^-4.

б) В серебряной монете при анализе параллельных проб получено следующее содержание серебра (%): 90,04; 90,12; 89,92; 89,94; 90,08 ; 90,02.

в) При определении сурьмы в сплаве титриметрическим методом получены данные(%): 11,95; 12,03; 11,98; 12,04.

г) При определении концентрации перманганата калия тремя студентами получены следующие результаты (моль/л):

0,1013; 0,1012; 0,1012; 0,1014;

0,1015; 0,1012; 0,1012; 0,1013;

0,1013; 0,1015; 0,1015; 0,1013.

4. Статистически значимо ли различаются результаты приведенных методов анализа:

а) Массовую долю (%) CuO в минерале определили методом иодометрии и методом комплексонометрии. По первому методу получили результаты:

38,20; 38,00; 37,66. По второму: 37,70; 37,65; 37,55.

б) Содержание Fe₂O₃ в руде определили перманганатометрическим методом и методом комплексонометрии. При этом получили следующие результаты(%): 1)60,12; 61,00; 61,25; 2)58,75; 58,90; 59,50.

5.Студент получил следующие результаты определения концентрации раствора HCl (моль/л): 0,1003; 0,1004; 0,1003; 0,1008. Следует ли исключить выпадающий результат?

6.Определяя константу диссоциации кислоты, химик получил следующие значения: 4,27·10^-4; 4,67·10^-4; 4,18·10^-4. Должен ли он оставить все результаты для дальнейшей обработки?

7. Получены следующие результаты определения меди в латуни (%): 12,29; 12,24; 12,48; 12,20. Решите вопрос об исключении выпадающего результата(Р=0,90).

Кислотно-основное равновесие

Расчет рН раствора по известным равновесным концентрациям растворенных веществ

При решении задач необходимо провести вычисления в следующей последовательности:

1) написать уравнение реакции взаимодействия веществ, при необходимости по ступеням;

2) перевести концентрации всех веществ в молярные;

3) рассчитать количество молей всех веществ;

4) на основании полученных данных определить состав раствора после протекания реакций и выбрать уравнение для расчета рН;

5) рассчитать объем раствора после смешения;

6) рассчитать концентрации веществ в образовавшемся после смешения растворе;

7) вычислить рН раствора.

Пример 1. Вычислить рН раствора, полученного при сливании:

а) 20 мл 0,12 М раствора NaCN и 15 мл 0,09 М раствора HCl.

Решение. Запишем уравнение реакции

NaCN+HCl = СHCN+NaCl

С целью выяснения состава раствора, образовавшегося после сливания, рассчитаем количества веществ в исходных растворах:

n₀ (NaCN) =20 · 10^-3 · 0.12 = 2.4 · 10^-3 моль

n₀ (HCl) =15 · 10^-3 · 0.09 = 1.35 · 10^-3моль.

Так как n₀(NaCN) › n₀(HCl), то NaCN находится в избытке, следовательно, в образовавшемся после сливания растворе будут находится NaCN и NaCN в следующих количествах:

n₁ (NaCN) = n₀ (NaCN) -n₀ (HCl) = 2,4 ∙10^-3 - 1,35 ∙ 10^-3 = 1,05 ∙10^-3 моль;

n₁ (HCN) = n₀ (HCl) = 1,35 ∙10^-3 моль;

Объем раствора (V) составит 20+15 = 35 мл.

Рассчитаем концентрации веществ в растворе:

С (NaCN) = 1,05 ∙10^-3/35 ∙10^-3 = 0,03 моль/л;

C (HCN) = 1,35 ∙10^-3/35 ∙10^-3 = 0,039 моль/л.

Исходя из состава раствора, выбираем формулу для расчета рН буферных растворов:

рН = pK_HCN-lg [C(HCN)/C(NaCN)] = 9,3-lg(0,039/0,03) = 9,18.

б) 11,25 мл 0,12 моль/л раствора NaCN и 15,0 мл 0,09 моль/л раствора HCl.

Решение.

n (NaCN) = 11,25 ·10^-3·0,12 = 1,35 ·10^-3 моль.

n (HCl) = 15,0 ·10^-3·0,09 = 1,35 ·10^-3 моль.

Так как n (NaCN)= n (HCl), то в образовавшемся после сливания растворе будет находиться только 1,35·10^-3 моль HCN.

Объем раствора(V) составит 11,25+15,0=26,25 мл.

Рассчитаем концентрацию HCN в растворе:

С(HCN )= 1,35 ·10^-3/26,25 ·10^-3=0,051моль/л.

Исходя из состава раствора, выбираем формулу для расчета рН слабых кислот:

рН=1/2рК_HCN – 1/2 lg (C(HCN))=1/2 · 9,3 – 1/2 · lg(0,051)=5,3;

в)20,0 мл 0,12 моль/л раствора NaCN и 35,0 мл 0,09 моль/л раствора HCl. Решение:

n₀ (NaCN) =20,0 ·10^-3 ·0,12=2,4 ·10^-3 моль.

n₀ (HCl) =35,0 ·10^-3 · 0,09=3,15 ·10^-3 моль.

n₀ (HCl) › n₀ (NaCN) , т.е. в избытке HCl, то в образовавшемся после сливания растворе будут находится HCl и HCN в следующих количествах:

n₁ (HCl)=35,0·10^-3· 0,09 – 20.0·10^-3·0,12=0,75·10^-3 моль.

n₁ (HCN)= 20,0 ·10^{- 3}·0,12=2,4·10^-3 моль.

Поскольку сильная кислота HCl подавляет диссоциацию слабой кислоты HCN, то рН определяется только ее концентрацией.

Объем раствора (V)составит 20,0+35,0=55,0 мл.

Рассчитаем концентрацию HCl в растворе:

С(HCl)=0,75·10^-3/55,0 C·10^-3=0,014 моль/л.

Исходя из состава раствора, выбираем формулу для расчета рН сильных кислот:

рН = - lg(C(HCl)) = - lg(0,014)=1,87.

Пример 2. Вычислить рН раствора, полученного при сливании 10, мл 0,1 моль/л раствора Na₂HAsO₄ и 16,0 мл 0,1 моль/л раствора HCl.

Решение:

После сливания растворов могут протекать следующие реакции:

Na₂HAsO₄+HCl=NaH₂AsO₄+NaCl (1)

NaH₂AsO₄+HCl=H₃AsO₄+NaCl (2)

Рассчитаем количества вещества в исходных растворах:

n(Na₂HAsO₄)=10,0 ·10^-3· 0,1 =1,0·10^-3 моль.

n(HCl)=16,0·10^-3· 0,1=1,6·10^-3 моль.

Так как Na₂HAsO₄ взят в недостатке , то все количество его прореагирует с HCl согласно уравнению (1) , и после протекания реакции (1) в растворе останется 1·10^-3 моль NaH₂AsO₄ и (1,6 -1,0) ·10^-3 =0,6·10^-3 моль HCl. Аналогично после реакции (2) в растворе будут находится H₃AsO₄ и NaH₂AsO₄ в следующих количествах:

n (NaH₂AsO₄) = 1,0·10^-3- 0,6 ·10^-3=0,4·10^-3 моль

n (H₃AsO₄) = 0,6·10^-3 моль.

Объем раствора после смешения составит 10+16=26 мл, или 26·10^-3л. Рассчитаем концентрации компонентов в растворе:

С(NaH₂AsO₄)=0,4·10^-3/26·10^-3=0,015 моль/л;

С(H₃AsO₄)= 0,6·10^-3/26·10^-3=0,023 моль/л.

Исходя из состава раствора , выбираем формулу для расчета рН буферных растворов:

рН=рК_1H3AsO4 - lg(C(H₃AsO₄) /C(NaH₂AsO₄))=2,22 – lg(0,023/0,015)=2.03.

Примечание:

Расчет рН растворов кислых солей проводится по следующей формуле:

рН=(рК_n+рК_n+1)/2

Индивидуальные задания .

Рассчитать рН раствора, полученного после смешения раствора 1 и раствора 2.

№	Раствор 1	Раствор 2
1.	20 мл 0,12 М NaOH	5,2 мл 0,24 М HCl
2.	20 мл 0,25 М NaOH	10,2 мл 0,5 М раствора сильной кислоты
3.	25 мл HNO3с титром 0,006128 г/мл	0,25 мл 0,1105 н NaOH
4.	25мл 0, 1120 М КОН	10,5 мл 0,1396 М HCl
5.	20 мл 0,175 н H2SO4	35 мл NaOH с титром 0,004000 г/мл
6.	100 мл 0,01 н HCl	100,1 мл 0,01 н NaOH
7.	25 мл 0,1 М HNO3	15,5 мл 0,11 М NaOH
8.	20,5 мл 0,102 н NaOH	15,5 мл 0,1 М H2SO4
9.	20,50 мл 0,1 М H3AsO4	45 мл 0,1 М КОН
10.	12 мл 0,3 М НСООН	15,00 мл 0,10 М NH4OH
11.	20,5 мл 0,1 М Na2CO3	20,25 мл 0,2 М HCl
12.	18,75 мл 0,112 М Н2C2 O4	40,00 мл 0,109 М NaOH
13.	20,25 мл 0,1 М НСООН	20,3 мл 0,1005 М КОН
14.	18,75 мл 0,1 М раствора гидразина	15,00 мл 0,125 М HCl
15.	19,25 мл 0,105 н. раствора гидроксиламина	10,10 мл 0,1 н. HCl
16.	25 мл 0,02723 М HCl	20 мл 0,1 М Na2HРО4
17.	25 мл 0,1 М Na3 РО4	50,0 мл 0,1 М HCl
18.	20 мл 0,11 М Na2HРО4	15 мл 0,05 М H2SO4
19.	22,5 мл 0,2 М К2НРО4	25 мл 0,2 М H2SO4
20.	20 мл 0,1 М КОН	10,5 мл 0,1 М H2SO4
21.	20 мл 0,1 М Са(ОН)2	19,75 мл 0,1 HCl
22.	20 мл 0,15 н. НСООН	40 мл 0,075 М КОН
23.	100 мл 0,1 н. раствора одноосновной кислоты (К=1*10-6)	99,9 мл 0,1 М раствора NaOH
24.	30 мл 0,15 н. СН3СООН	60 мл 0,075 М NaOH
25.	100 мл 0,1 н. НСООН	99,9 мл 0,1 М NaOH
26.	20,55 мл 0,1 М NH4OH	20,86 мл 0,0985 М HCl
27.	15 мл 0,1 н. Na2В4О7	15 мл 0,1 н. HCl
28.	20 мл 0,1036 М H3 РО4	15,82 мл 0,1307 М NaOH
29.	20 мл 0,1 М H3РО4	15,20 мл 0,1280 М NaOH
30.	17,5 мл 0,12 М H3РО4	35 мл 0,12 М КОН
31.	17,46 мл 0,1 М H3РО4	17,80 мл 0,1950 М NaOH
32.	25 мл 0,12 М H3РО4	30,00 мл 0,25 М КОН
33.	15,05 мл 0,1 М H3РО4	45,15 мл 0,1 М NaOH
34.	25,00 мл 0,1 М Na3 РО4	24,5 мл 0,2 М HCl
35.	24,30 мл 0,12 М Na3 РО4	40,52 мл 0,12 М HCl
36.	20 мл 0,125 М Na2CO3	24,00 мл 0,1 М HCl
37.	19 мл 6,2н СН3СООН	1 мл 2 н СН3СООNa
38.	15 мл 0,05 н СН3СООН	15 мл 0,01 н СН3СООNa
39.	125 мл 0,2М NH4OH	125 мл 0,2М NH4Cl
40.	12 мл 0,2М NH4OH	12 мл 0,5М NH4Cl
41.	17 мл 0,2М NH4OH	17 мл 1М NH4Cl
42.	50 мл 0,05М NH4OH	60 мл 0,01н HCl
43.	15 мл 0,05 н СН3СООН	20 мл 0,02 н КОН
44.	25 мл 0,1 н NH4OH	15 мл 0,1н НNO3

1. Вычислите рН следующих растворов:

• 0,4% гидроксида натрия, плотность 1,002 г/см^З;

• 0,74% гидроксида калия, плотность 1,004 г/см^з;

• 0,1 М азотистой кислоты;

• 0,2 М цианистоводородной кислоты;

• 0,01 М муравьиной кислоты;

• 0,1 М фенола;

• 0,02 М бензойной кислоты;

• 0,1 М гидроксиламина;

• 0,2 М анилина.

2. Вычислите рН среды в 0,1 М растворах следующих протолитов: цианида калия; сульфита натрия; гидросульфита натрия; карбо­ната натрия; гидрокарбоната натрия; карбоната аммония; фосфа­та натрия.

3. Вычислите рН среды, если навеску 0,05 г нитрата аммония ра­створили в 100 мл раствора.

4. Вычислите степень диссоциации в 0,01 М растворах: азотистой кислоты; уксусной кислоты; синильной кислоты; гидроксида ам­мония; анилина; гидроксиламина.

5. Вычислите кажущуюся степень диссоциации в 0,5 М растворах: а) соляной кислоты при рН 0,37; б) гидроксида калия при рН 13,5.

6. Вычислите концентрацию ионов водорода и гидроксила в ра­створе, рН которого равен: 2; 9; 6.

7. Вычислите рН смеси, содержащей равные объемы 5% растворов уксусной

кислоты и ее натриевой соли.

2. Вычислите рН 0,001 М раствора гидроксида аммония в присут­ствии

0.1М раствора хлорида аммония.

2. Вычислите рН 0,01 М раствора иодноватистой кислоты (HIO) в

присутствии 0,1 М раствора ее соли (NaIO).

10.Вычислите рН смеси аммиака и хлорида аммония, если она при­готовлена

из 0,1 М растворов этих веществ в отношении 1 : 9.

11. Вычислите рН смеси, если к 200 мл 0,1 М раствора NH₄ ОН доба­вить

2,14г хлорида аммония.

12. Какую навеску хлорида аммония следует растворить в 100 см^З

раствора, чтобы рН раствора был равен 6?

13. В каком объеме следует растворить навеску ацетата натрия 0.03г ,

чтобы получить раствор с рН 8 ?

14. Приготовьте 30 мл буферного раствора с рН 9,0.

15. Сколько грамм безводного ацетата аммония надо добавить к 200 мл 0,1

М раствора уксусной кислоты, чтобы получился буферный раствор с рН

3,87?

16. Вычислите рН 0,0625 М раствора этиламина С₂Н₅NНзОН, если

подвижность иона С₂Н₅NН_з ⁺ равна 58,6, а эквивалентная элект­рическая

проводимость этого раствора составляет 20,99 Ом^-1 см² .

17. Вычислите рН 0,1 М раствора НI0₃, если удельная электропро­водимость

этого раствора 4,02 Ом·¹ см·¹, а подвижность иона IO₃ ^- 41 Ом·¹ см².

18. Вычислите константу диссоциации гидроксида аммония, если

эквивалентная электрическая проводимость 0,0082 М раствора NH₄0H

равна 12,43 Ом·¹ см² .

Равновесие в системе осадок-раствор.

Гетерогенная система состоит из двух фаз: насыщенного раствора электролита и осадка. В этой системе устанавливается динамическое равновесие:

BaSO₄↓↔Ba²⁺+ SO₄^2-

К этой равновесной системе применим закон действия масс, исходя из которого можно сформулировать правило произведения растворимости(ПР):

Произведение концентраций ионов труднорасворимого электролита в его насыщенном растворе есть величина постоянная при данной температуре:

ПР_BaSO4=[Ba²⁺]∙[SO₄^2-]

Если в формуле имеются стехиометрические коэффициенты, то они входят в уравнение как показатели степени, в которые необходимо возвести концентрации ионов, например:

ПР_Ca3(PO4)2=[Ca²⁺]³∙[PO₄^3-]²

Произведение растворимости характеризует растворимость вещества: чем больше значение ПР, тем больше растворимость.

При более точных расчетах необходимо вместо концентраций ионов использовать значения активностей, учитывающих электростатические взаимодействия между ионами.

Активности ионов пропорциональны концентрациям:

а =f ∙C.

Здесь f =a/C – коэффициент активности, зависящий от концентраций и зарядов всех ионов в растворе, а также от собственного заряда иона. Для нахождения коэффициентов активности сначала рассчитывают ионную силу раствора I по формуле

Здесь C_i Z_i – молярные концентрации и заряды всех ионов в растворе.

1. Расчет ПР по растворимости.

Пример 1. Вычислить произведение растворимости иодида серебра , если растворимость этой соли при температуре 25^◦С равна 2.865 ∙10^-6 г/л.

Решение. Химическое равновесие в насыщенном растворе AgI описывается уравнением:

AgI↔Ag⁺+I^-

Запишем выражение произведения растворимости для иодида серебра:

ПР_AgI=[Ag⁺]∙[I^-]

Вычислим растворимость иодида серебра (моль/л). Так как молярная масса AgI составляет 234.772 г/моль, то концентрация AgI в растворе составит

[AgI]=2.865∙10^-6/234.772=1.22∙10^-8моль/л.

При диссоциации каждого моля иодида серебра образуется 1 моль Ag⁺ и 1 моль I^-. Следовательно, их концентрации равны:

[Ag⁺]=[I^-]=[AgI]=1.22∙10^-8 моль/л.

Подставляя значения [Ag⁺] [I^-] в уравнение произведения растворимости , получим:

ПР_AgI= 1.22∙10^-8∙1.22∙10^-8=1.5 ∙10^-16.

Пример 2. Вычислить произведение растворимости Ag₂CrO₄ , если в 100 мл насыщенного раствора его содержится 0.002156г.

Решение. Найдем растворимость хромата серебра (моль/л):

в 100 мл насыщенного раствора содержится 0.002156 г соли

в 1000 мл ---------------------------------------------- х г соли

х=1000∙0.002156/100=0.02156 г/л.

Молярная масса Ag₂CrO₄ равна 331.73 г/моль, тогда растворимость Ag₂CrO₄ (моль/л) будет

[Ag₂CrO₄]=0.02156/331.73 моль/л=6.5∙10^-5моль/л.

Хромат серебра диссоциирует следующим образом:

Ag₂CrO₄↓↔2Ag⁺+ CrO₄^2-

Тогда

[Ag⁺]=2∙6.5∙10^-5=1.3∙10^-4моль/л;

[CrO₄^2-]=6.5∙10^-5 моль/л;

ПР _Ag2CrO4=[Ag⁺]² [CrO₄^2-]=(1.3∙10^-4)²∙6.5∙10⁵≈1.1∙10^-11.

2. Расчет растворимости осадков в воде.

Пример 3. Вычислить растворимость оксалата кальция, массовую концентрацию ионов Са²⁺ и массу кальция в 100 мл раствора, если произведение растворимости его равно 2.57 ∙ 10^-9.

Решение. Химическое равновесие в насыщенном растворе СаС₂О₄ описывается уравнениями:

СаС₂О₄↓↔ Са²⁺+ С₂О₄^2-

ПР СаС₂О₄ ↔[Ca²⁺]∙[C₂O₄^2-]

Обозначим растворимость СаС₂О₄ через х моль/л. При диссоциации х молей СаС₂О₄ образуется х молей Са²⁺ и х молей С₂О₄^2-. Подставляя эти значения в уравнение произведения растворимости, получим

ПР СаС₂О₄ =х∙х=2.57∙10^-9;

Х²=2.57∙10^-9;

Х==5.07∙10^-5моль/л.

Чтобы найти растворимость СаС₂О₄ (г\л), необходимо молярную растворимость (моль/л) умножить на молярную массу СаС₂О₄:

5,07·10^-5·128,1≈6,5·10^-3г/л.

Чтобы найти массовую концентрацию ионов Са²⁺, нужно умножить молярную растворимость на атомную массу Са²⁺:

5,07·10^-5·40,08≈2·10^-3г/л.

Массу кальция в 100мл раствора находим из пропорции:

в1000 мл раствора-- 2·10^-3 г кальция,

в100 мл раствора -- х г кальция,

х=2·10^-3·100/1000=2·10^-4г.

1.3.Задачи на применение условия выпадения осадка.

Пример 4.При какой молярной концентрации хромата натрия начнется выпадение осадка из 0,001М раствора нитрата свинца?

Решение: Составим уравнение диссоциации хромата натрия и нитрата свинца:

Na₂CrO₄ →2 Na⁺ + CrO₄^2-

Pb(NO₃)₂→Pb²⁺ + 2NO₃^-

Следовательно, молярные концентрации ионов Pb²⁺ CrO₄^2- совпадают с молярными концентрациями солей.

Составим уравнение диссоциации хромата свинца :

PbCrO₄↓↔ Pb²⁺+ CrO₄^2-

ПР _PbCrO4=[Pb²⁺]·[ CrO₄^2-]=1,8·10^-14.

Следовательно, [ CrO₄^2-]=ПР _PbCrO4/[Pb²⁺]=1,8·10^-14/0,001=1,8·10^-11моль/л.

С _Na2CrO4=[ CrO₄^2-]=1,8·10^-11моль/л.

Пример 5. Выпадет ли осадок при сливании 100 мл фильтрата, оставшегося от осаждения иодида свинца , с 200 мл 0,1М раствора хромата натрия?

Решение:ПР_PbI2=[Pb²⁺]·[I^-]²=1,1·10^-9.

Химическое равновесие в насыщенном растворе PbI₂ описывается уравнением

PbI₂↓↔Pb²⁺+ 2I^-

Если растворимость PbI₂ равна х моль/л, то [Pb²⁺]=х моль/л, а [I^-]=2х моль/л. Следовательно, ПР_PbI2=х·(2х)²=4х³=1,1·10^-9;

х=³√1,1·10^-9/4=6,5·10^-4моль/л.

После сливания растворов объем составит

V=100+200=300 мл,

а концентрация ионов Pb²⁺ уменьшится :

С ( PbI₂) =6,5·10^-4·100/300=2,17·10^-4моль/л.

Соответственно уменьшится и концентрация иона CrO₄^2-:

С (CrO₄^2-)=0,1·200/300=0,067 моль/л.

Для ответа на вопрос о возможности выпадения осадка найдем произведение концентраций (ПС) ионов Pb²⁺ и CrO₄^2- и сравним полученное значение с ПР (PbCrO₄ )=1,8·10^-14:

ПС=2,17·10^-4·0,067=1,45·10^-5>1,8·10^-14.

следовательно, осадок не выпадет.

1.4. Расчет растворимости осадков в присутствии одноименных ионов.

Пример 6. Вычислить концентрацию ионов серебра в насыщенном растворе хлорида серебра, к 1 л которого прибавлено: а) 1·10^-4 моль КСl ; б) 0,1 моль КСl.

Решение. а) Хлорид-ионы образуются при диссоциации хлорида серебра и при диссоциации хлорида калия. Тогда будем иметь:

[Ag⁺]·([Cl^-]_AgCl+[Cl^-]_KCl)=ПР_AgCl=1,56·10^-10

Так как [Ag⁺]=[Cl^-]_AgCl, то

[Ag⁺]²+[Cl^-]_KCl·[Ag⁺]-1,56·10^-10=0

Подставляя значение концентрации KCl и решая квадратное уравнение, получим:

[Ag⁺]=-10^-4/2+=1,54·10^-6моль/л.

б) В данном случае значение [Cl^-]_KCl существенно превышает величину

[Cl^-]_AgCl , поэтому величиной [Cl^-]_AgCl можно пренебречь. Тогда будем иметь [Ag⁺]· [Cl^-]_KCl=ПР _AgCl=1,56·10^-10;

[Ag⁺]= ПР _AgCl/[Cl^-]_KCl=1,56·10^-10/0,1=1,56·10^-9моль/л.

1.5.Расчет растворимости осадка в присутствии разноименных ионов ( солевой эффект).

Пример 7. Вычислить растворимость хлорида серебра в 0,01М растворе Ca(NO₃)₂.

Решение. При решении данной задачи необходимо учитывать солевой эффект. Запишем ПР_AgCl с учетом коэффициентов активности:

ПР_AgCl=a_Ag+·a_Cl-=C_Ag+·f_Ag+·C_Cl-·f_Cl-.

Если обозначить концентрацию хлорида серебра через х моль/л, то можно записать ПР_AgCl=х²·f_Ag+·f_Cl-.

Для нахождения коэффициентов активности рассчитаем ионную силу 0,1 моль/л раствора Ca(NO₃)₂.

Запишем уравнение диссоциации нитрата кальция:

Ca(NO₃)₂↔Ca²⁺+2NO₃^-

Следовательно,

C(Ca²⁺)=C(Ca(NO₃)₂)

C(NO₃^-)=2C(Ca(NO₃)₂)

Таким образом,

I=1/2∑(C_iz_i²)=1/2(0,01·2²+0,02·1²)=0,03моль/л.

Коэффициент активности рассчитаем по формуле

.

Рассчитанная величина f=0,771 для однозарядных ионов Ag⁺ и Cl^- совпадает. Следовательно,

х=/0,771=1,73·10^-5моль/л.

Задачи для самостоятельного решения.

1.Вычислить произведение растворимости соли:

а) CaF₂, если массовая концентрация насыщенного раствора соли составляет 0,017 г/л.

б)MgNH₄PO₄, если при анализе 1000мл насыщенного раствора найдено 7.9 мг этой соли.

в)BaCrO₄, если массовая концентрация соли в насыщенном растворе составляет 2,7 мг/л.

г) BaCrO₄, если 400 мл насыщенного раствора содержат 1,22·10^-3г этой соли.

д) MgNH₄PO₄, если в 400 мл насыщенного раствора содержится 3,4 ·10^-3г этой соли.

2.Рассчитать массовую концентрацию соли ВаСО₃ в насыщенном растворе.

3.ПР(Са(РО₄)₂)=2,0·10^-29, ПР(Се₂(С₂О₄)₃)=2,5·10^-29. Вычислить массовую концентрацию катиона в насыщенном растворе каждой из этих солей.

4.Рассчитать массу Pb²⁺в 10мл насыщенного раствора PbI₂, если ПР(PbI₂=1,1·10^-9.

5.Какая из двух солей более растворима и во сколько раз:

а)BaSO₄ BaCO₃?

б)PbSO₄ PbI₂ ?

в)AgCl Ag₃PO₄?

г)Ce₂(C₂O₄)₃ ZnCO₃?

д)Ca₃(PO₄)₂ CaCO₃?

6.В каком насыщенном растворе и во сколько раз меньше содержится ионов серебра:

а)AgCl AgBr?

б)Ag₂CrO₄ Ag₃PO₄?

в)Ag₂CO₃ AgBO₃?

7.ПР иодата серебра равно 3·10^-8, а иодата бария—1,5·10^-9. В каком из этих насыщенных растворов концентрация иодат-ионов больше и во сколько раз?

8.Образуется ли осадок при смешении:

а)равных объемов 10^-3М растворов NaCl и AgNO₃?

б)100мл 10^-3М раствора PbSO₄ и 200мл раствора NaI с концентрацией 0,15 г/л?

в)равных объемов 10^-3М растворов SrCl₂ и K₂SO₄?

г)насыщенного раствора CaSO₄ с равным объемом раствора (NH₄)₂C₂O₄ с концентрацией 2,5·10^-2г/л?

д)15мл 0,02М раствора хлорида бария с 5мл 0,01М раствора серной кислоты?

е)0,02н раствора хлорида кальция с равным объемом 0,02н раствора карбоната натрия?

ж)10мл 0,001н раствора хлорида стронция с 1мл 0,001М раствора хромата калия?

9.Вычислить массовую концентрацию насыщенного раствора хромата серебра в воде и в 0,01М растворе K₂CrO₄.

10.Вычислить молярную растворимость осадка CaC₂O₄ в 10^-4М растворе (NH₄)₂C₂O₄.

11.Во сколько раз растворимость хромата бария в воде больше, чем в 0,01М растворе K₂CrO₄?

12.Во сколько раз растворимость CaC₂O₄ в 10^-2М растворе (NH₄)₂C₂O₄ меньше, чем в воде?

13.Как изменится концентрация ионов серебра в литре насыщенного раствора хлорида серебра, если к нему прибавить равный объем 0,005н раствора соляной кислоты?

14. Во сколько раз растворимость оксалата кальция меньше в 0,002М растворе оксалата натрия , чем в воде?

15.сравнить растворимость оксалата кадмия в чистой воде и в 0,05М растворе оксалата натрия.

16.Как изменится растворимость оксалата кальция в воде по сравнению с растворимостью его в 0,1н растворе хлорида натрия?

17. По величине ПР вычислить растворимость хлорида серебра (г/л) в 0,1М растворе нитрата калия с учетом коэффициентов активности.

18.Как изменится растворимость карбоната кальция в воде по сравнению с растворимостью его в 0,1н растворе хлорида калия?

19.Как изменится растворимость сульфата бария в воде по сравнению с растворимостью его в 0,15н растворе иодида натрия?

20.Вычислить растворимость иодида серебра в 1М растворе нитрата алюминия.

21.Как изменится растворимость карбоната бария в воде по сравнению с растворимостью его в 0,3н растворе иодида калия?

22.Смесь 10мл 0,1М раствора хлорида натрия и 1мл 0,01М раствора бромида натрия довели водой до 10л и прибавили 1мл 0,01М раствора нитрата серебра. Будет ли образовываться осадок и какого состава? ПР(AgCl)=1,78·10^-10, ПР(AgBr)=5,3·10^-13.

23.При каком значении рН начнется образование осадка гидроксида марганца (2) из раствора, в котором концентрация хлорида марганца(2) равнв 10^-2 моль/л? При каком значении рН осаждение гидроксида марганца можно считать полным? ПР(Mn(OH)₂)=2·10^-13.

24.При каком значении рН начнется образование осадка гидроксида алюминия из 2·10^-2М раствора хлорида алюминия? ПР(Al(OH)₃)=1·10^-32.

25.К 10мл насыщенного раствора сульфата кальция прибавили 5мл насыщенного раствора сульфата бария. Определите концентрацию сульфат-ионов в полученном растворе. ПР(CaSO₄)=2,5·10^-5,ПР(ВаSO₄)=1,1·10^-10.

26.При получении осадка оксалата кальция к 1л 0,2М раствора хлорида кальция прибавили 400мл 0,2М раствора оксалата аммония. Сколько граммов кальция осталось неосажденными? ПР(CaC₂O₄)=2·10^-9.

27.Как изменится величина ПР сульфата бария, если его растворимость при изменении температуры увеличится в два раза?

Окислительно-восстановительное равновесие.