уч.практика
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Башкирский государственный университет»
ОТЧЕТ ПО УЧЕБНОЙ ПРАКТИКЕ
Егоровой Анны Евгеньевны, 22 гр
(Ф.И.О. студента, группа)
Направление подготовки 010100 «Математика»
Профиль"Вещественный, комплексный и функциональный анализ “
Факультет_Математики и информационных технологий
Кафедра Математического анализа
Уфа-2014
I.Учебная практика по теории функций комплексного переменного.
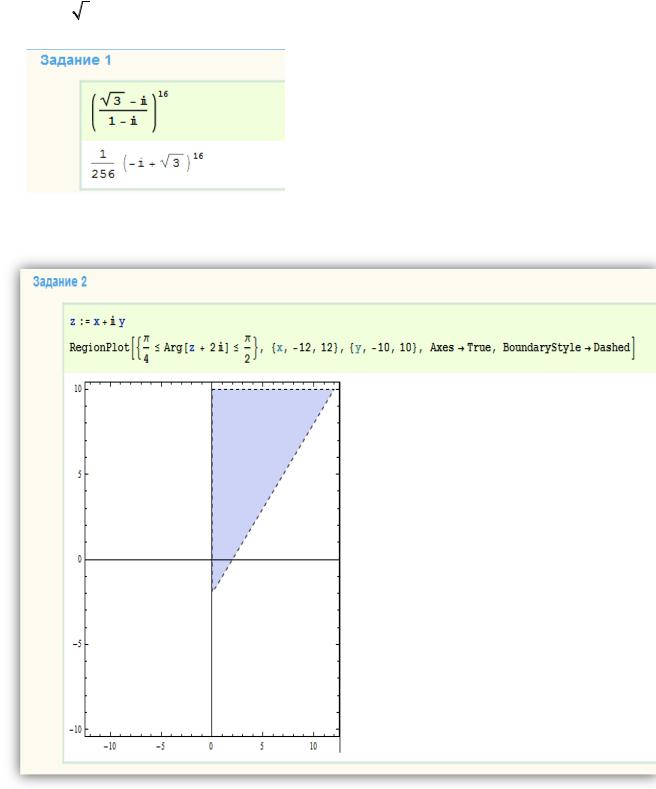
1.Вычислить, используя математические пакеты Maple, MathCad или другие значение
|
|
|
i 16 |
||
|
3 |
||||
выражения |
|
|
|
|
|
1 i |
|||||
|
|
||||
|
|
|
|||
2.Указать (используя математические пакеты) на комплексной плоскости множество
точек, удовлетворяющих условию |
|
arg(z 2i) |
|
|
4 |
|
2 |
3.Вычислить, используя математические пакеты 1 i i
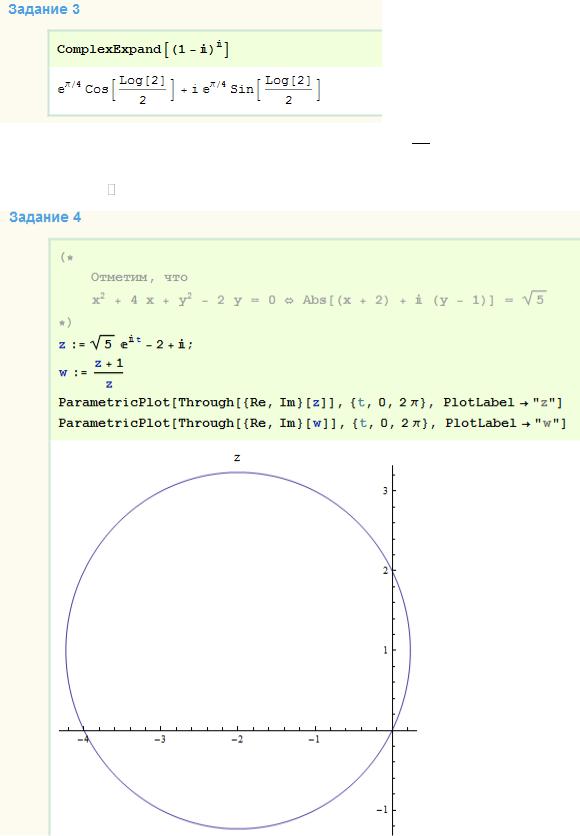
4. Найти область, которая получается при преобразовании области D с помощью функции w f (z) , используя математические пакеты, если
|
|
: x2 4x y2 2y 0} , |
f (z) |
z 1 |
|
|
D {z x iy |
|
|||||
z |
||||||
|
|
|
|
|||
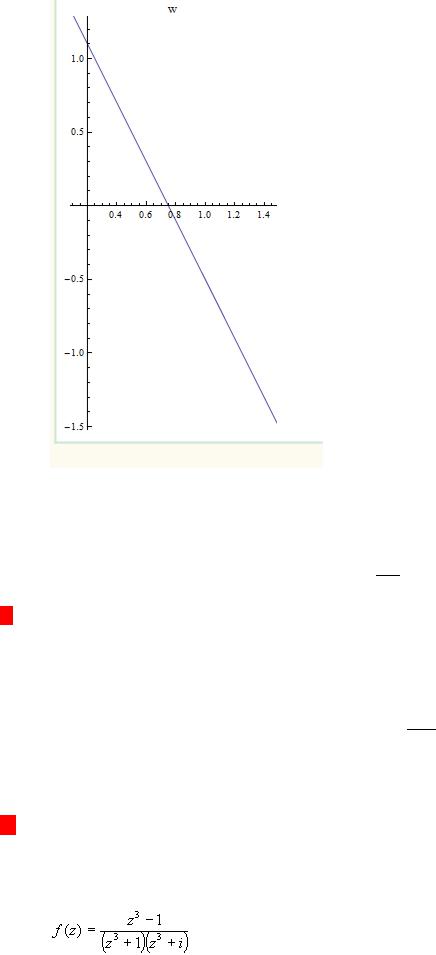
5.Тест (Особые точки)
1. Определить характер точки z = 0 для функции:
а) правильная точка; б) существенно особая точка; в) простой полюс; г) полюс 3 порядка;
2. Определить порядки полюсов для следующей функции
А)z=0-‘3’; Б)z=1-‘1’; В)z=πk-‘1’; Г)z=0-‘1’,z=πk-‘3’; Д)z=1-‘1’;z=πk-‘1’.
3.Определить тип всех конечных особых точек функции:
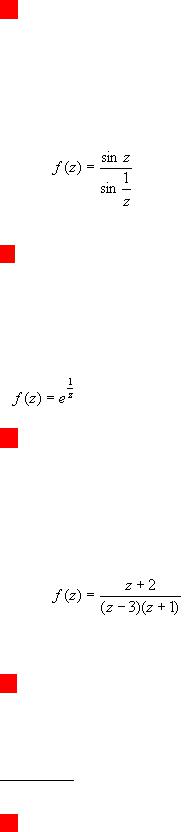
А) изолированные и полюсы; Б) полюсы; В) существенно особые;
Г) особые и изолированные; Д) полюса и изолированные.
4.Определить тип всех конечных особых точек функции
А) особые и изолированные; Б) изолированные и полюсы; В) существенно особые; Г) полюса и изолированные; Д) полюсы.
5. Найти все особые точки и определить их тип:
А)z=0- существенно особые; Б)z=1-изолированная точка;
В)z =0,z=1-полюс;
Г)z=1-полюс; Д)z==0-изолированная точка.
6. Найти особые точки функции
А)z=-3; Б)z=1,z=3; В)z=3,z=-1; Г)z=-1; Д)z=-1,z=-3.
7. Найти особые точки функций и определить их тип (для полюсов указать порядок):
А) z =1— полюс 3 порядка z = 0 и z = -1— полюсы 1 порядка; Б) z = -i — существенно особая точка;
В) z =1— полюс 1 порядка z = 0 полюсы 1 порядка; Г) z = 0 и z = -1— полюсы 1 порядка;
Д)z =1— полюс 3

8. Найти особые точки функций и указать на характер:
А) z = 0— полюс 3 порядка, z = ∞ –существенно особая точка; Б) z = 0 –простой полюс,z=±2i — полюсы 2 порядка;
В) z = 0— полюс 3 порядка; Г) z = 0 –простой полюс;
Д) z=±2i — полюсы 2 порядка.
9. Найти особые точки функций и указать их характер:
А) z = 0— существенно особая точка; Б) ±1,±i — простые полюсы;
В) ∞— правильная точка;
Г) ±1,±i — простые полюсы, ∞— правильная точка;
Д) z = 0— существенно особая точка, ∞— правильная точка.
10. Найти особые точки функции:
А) z = 0 — существенно особая точка; Б) ∞— правильная точка;
В) ±1,±i — простые полюсы; Г) z = 0— полюс 3 порядка;
Д) z = 0— полюс 3 порядка, z = ∞ –существенно особая точка.
II.Учебная практика по дифференциальным уравнениям.
10.Рассмотрим систему
,где f(x
(0,0,0); (1,0,-1); (-1,0,1)- точки равновесия
1)(0,0,0) (Линиаризируем)

|A-ƛE|= =
По Th Стадона решение (0,0,0) – неустойчиво , т.к не все коэффициенты положительны.
2)(1,0,-1) (Линиаризируем)
|A-ƛE|= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Составим матрицу Гурвица |
|
|
|
, где |
=1; |
|
|
|
|
; = |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
G= |
|
|
|
|
|
|
|
, где |
|
>0; |
=1>0. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По критерию Рауса-Гурвица решение устойчивое.
3)(-1,0,1) (Линиаризируем)
Т. к матрица совпадает с матрицей из пункта (2) , то решение устойчиво.
11.Построить (с использованием к-л математического пакета, например MAPLE)решение x(t)задачи Коши на промежутке 0≤t≤10
>
>
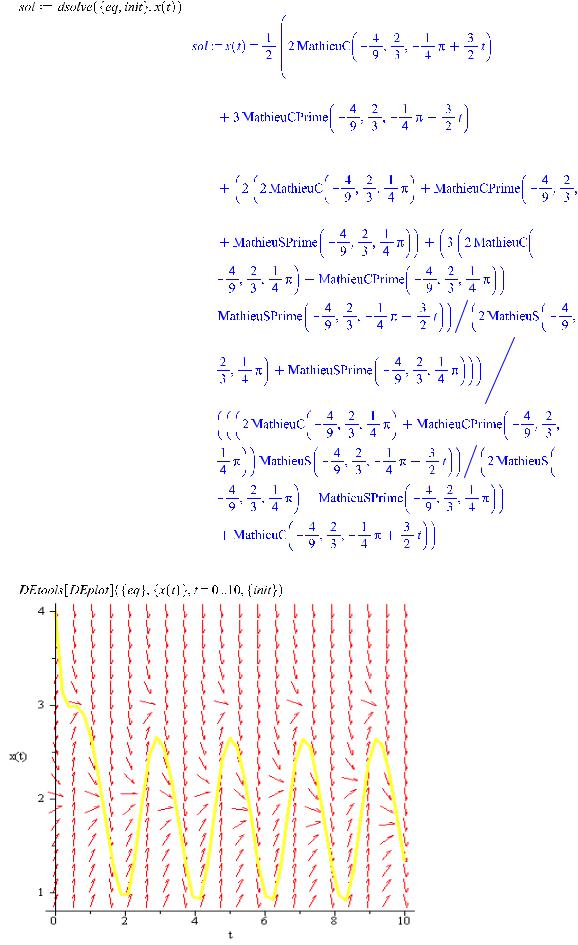
>
>
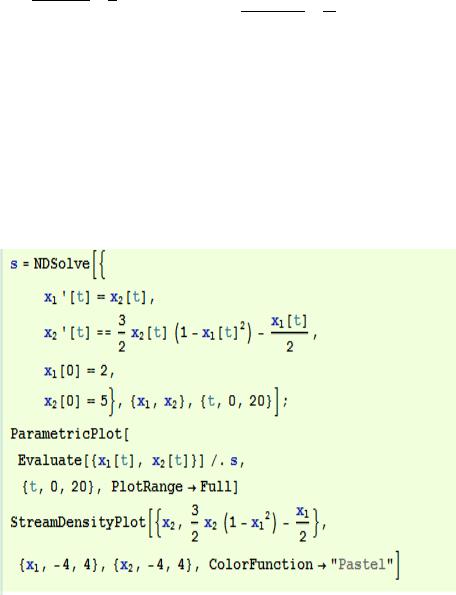
12.Перейти от ДУ 2-го порядка |
+ f(y, ) + g(y)=0 к автономной системе х =F(x) |
(x ϲ ) на основе замены: =y; |
= . Найти точки равновесия полученной системы, |
определить их тип, выяснить характер устойчивости. Построить (с помощью математический пакетов) на фазовой плоскости ( ; ) траекторию решения x(t) полученной системой на промежутке 0≤t≤20, соответствующей решению задачи Коши для ДУ. Построить портрет системы:
(0,0)- нулевая точка равновесия.
Линиаризируем: |
=> A= |
=> |A-ƛE|= |
= |
|
=> устойчивый узел |