Физический и математический маятник

Физическим маятником называется твердое тело, шарнирно закрепленное на горизонтальной оси и движущееся под действием силы тяжести (рис. 1).

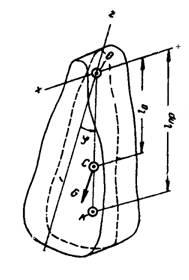
Рисунок 1.

Точка О пересечения оси вращения х с плоскостью, проходящей через центр масс тела и перпендикулярной оси х, называется точкой подвеса маятника.

Дифференциальное уравнение колебаний физического маятника

где l_o=OC - расстояние от центра масс С до точки О; G - вес тела.

Дифференциальное уравнение малых колебаний физического маятника (при φ≈sin φ)

Кинематическое уравнение малых колебаний физического маятника

где φ₀ и ω₀ - начальный угол отклонения от вертикали и начальная угловая скорость маятника;

амплитуда колебаний;

начальная фаза;

круговая частота физического маятника.

При амплитуде а≤8° погрешность при рассмотрении колебаний физического маятника как малых составляет менее 0,1%, при амплитуде а≤22° погрешность менее 1%.

Период малых колебаний физического маятника:

Математический маятник - сосредоточенная масса на конце гибкой нерастяжимой нити длиной l - является частным случаем физического маятника.

Дифференциальное уравнение малых колебаний математического маятника

Период малых колебаний математического маятника

Приведенной длиной l_пр физического маятника называется длина такого математического маятника, который имеет одинаковый период колебаний с данным физическим маятником:

где m - масса тела; r_Xc - радиус инерции тела относительно центральной оси х_с, параллельной оси подвеса х.

Точка К, лежащая на расстоянии l_пр от центра подвеса О на прямой ОС, называется центром качания. Если центр качания К поменять местами с центром подвеса О, период малых колебаний не изменится.

Если менять положение точки подвеса О физического маятника, период колебаний его может меняться (рис. 2) от ∞ (при l₀=0 и l₀→∞) до некоторой минимальной величины Т_мин при l₀=r_Хс:

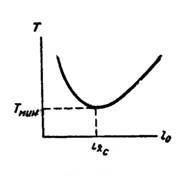
Рисунок 2.

Комплексная форма представления колебаний.

Формула Эйлера для комплексных чисел , где , поэтому уравнение гармонического колебания  можно записать в экспоненциальной форме: . Вещественная часть представляет собой ()смещение  при гармоническом колебании  обычно пишут .

10