Teoria_veroyatnostey_Variant_14

Задача 1.

В группе из n студентов, среди которых k девушек, выбирается делегация из m человек. Найти вероятность того, в делегации окажется не более одной девушки.

n = 10; k = 4; m = 4.

Решение.

Событие А («не более одной девушки») является объединением двух событий: В – «не окажется ни одной девушки» и С – «окажется одна девушка». Таким образом: Р(А) = Р(В) + Р(С).

Найдем вероятности событий В и С.

Выбрать делегацию из общего количества студентов можно способами.

Выбрать делегацию, в которой не будет девушек, можно способами.

Выбрать делегацию с одной девушкой можно способами.

Имеем:

Ответ: 19/210.

Задача 2.

Бросаются две игральные кости. Определить вероятность того, что произведение числа очков 1) не превосходит 6; 2) делится на 6.

Решение.

Рассмотрим все комбинации произведений числа очков, которые могут выпасть при бросании 2 игральных костей. Имеем:

1: ⚀⚀ (1 комбинация);

2: ⚁⚀ или ⚀⚁ (2 комбинации);

3: ⚀⚂ или ⚂⚀ (2 комбинации);

4: ⚀⚃ или ⚃⚀ или ⚁⚁ (3 комбинации)

5: ⚀⚄ или ⚄⚀ (2 комбинации);

6: ⚀⚅ или ⚅⚀ или ⚁⚂ или ⚂⚁ (4 комбинации);

8: ⚁⚃ или ⚃⚁ (2 комбинации);

9: ⚂⚂ (1 комбинация);

10: ⚁⚄ или ⚄⚁ (2 комбинации);

12: ⚁⚅ или ⚅⚁ или ⚃⚂ или ⚂⚃ (4 комбинации);

15: ⚂⚄ или ⚄⚂ (2 комбинации);

16: ⚃⚃ (1 комбинация);

18: ⚂⚅ или ⚅⚂ (2 комбинации);

20: ⚃⚄ или ⚄⚃ (2 комбинации);

24: ⚃⚅ или ⚅⚃ (2 комбинации);

25: ⚄⚄ (1 комбинация);

30: ⚄⚅ или ⚅⚄ (2 комбинации);

36: ⚅⚅ (1 комбинация).

Общее число возможных комбинаций: N = 36/

1) Нас удовлетворяют произведения, равные 1, 2, 3, 4, 5 и 6. Таких комбинаций М = 14. Таким образом:

2) Нас удовлетворяют произведения, равные 6, 12, 18, 24, 30 и 36. Таких комбинаций М = 14. Таким образом:

Ответ: 1) 7/18; 2) 13/36

Задача 3.

Найти вероятность того, что сумма двух наудачу взятых положительных правильных дробей не больше а, а их произведение не больше b.

а = 0,8; b = 3/25.

Решение.

Имеем: х + у ≤ 0,8 и х · у ≤ 0,12.

Решая графически систему неравенств:

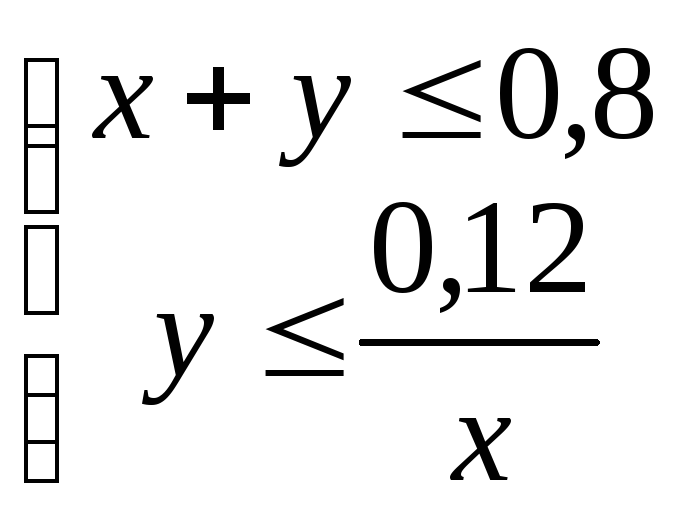получим фигуру, заштрихованную на рисунке.

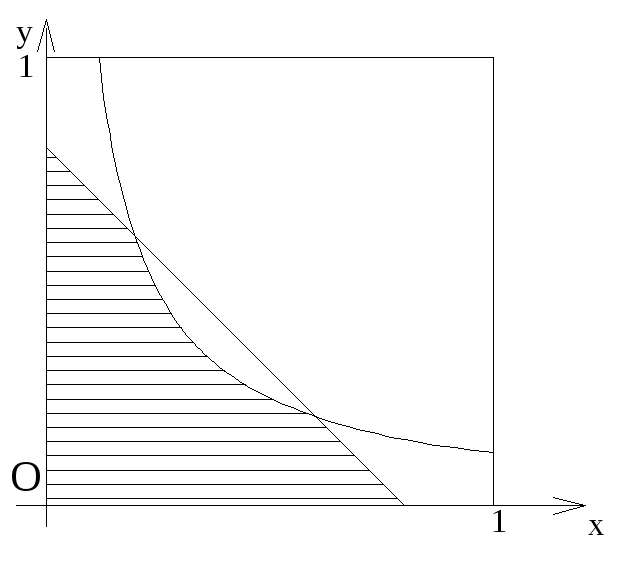
Таким образом, искомая вероятность равна отношению площади заштрихованной фигуры к площади квадрата со стороной 1.

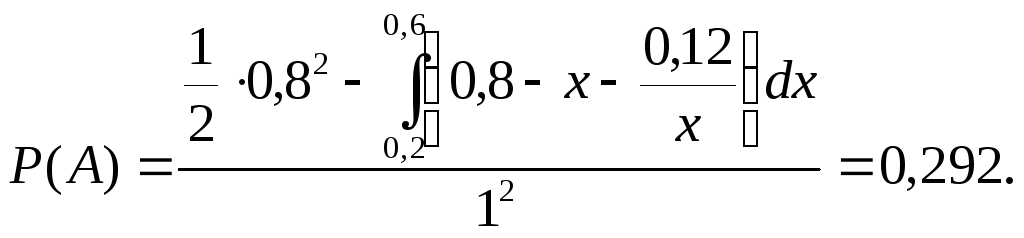
Ответ: 0,292.

Задача 4.

В первой урне N₁ белых и М₁ черных шаров, во второй – N₂ белых и М₂ черных. Из первой урны во вторую переложили один шар, затем из второй урны вынули один шар. Определить вероятность того, выбранный из второй урны шар – белый.

N₁ = 3; М₁ = 2; N₂ = 4; М₂ = 4.

Решение.

Введем гипотезу Н: переложенный шар – белый. Вероятности гипотез равны:

Для условных вероятностей имеем:

По формуле полной вероятности, находим:

Ответ: 23/45.

Задача 5.

В магазине три вида стиральных машин. Их количества относятся как 5:3:2. Покупатель может купить стиральную машину I вида с вероятностью 0,1; II-го вида – с вероятностью 0,2 III-го вида – с 0,15.

а) Найти вероятность того, что наудачу выбранный покупатель приобретет стиральную машину;

б) Покупатель приобрел стиральную машину. Какого вида вероятнее всего она оказалась?

Решение.

а) Пусть событие А – «покупатель приобрел стиральную машину». Введем гипотезы: Н_i – выбрана стиральная машина i-го вида . Эти гипотезы по условию равны:

Для условных вероятностей покупки стиральной машины i-го вида имеем:

Таким образов, по формуле полной вероятности, получаем:

б) Условные вероятности гипотез Н_i, при условии, что покупатель приобрел стиральную машину, найдем по формулам Байеса:

Вероятнее всего покупатель купил стиральную машину II-го вида.

Ответ: а) 0,14; б) II-го вида.

Задача 6.

Опыт состоит в бросании монеты. Монету бросают n раз. Вероятность выпадения «герба» при одном выбросе равна р. Составить ряд распределения для случайной величины Х – количества заработанных очков, если количество очков в s раз больше количества выпадений «герба» в серии из n бросков. Определить вероятность того, что будет набрано:

а) ровно k очков;

б) не более k очков;

в) максимальное число очков;

г) минимальное число очков.

Найти; F(х), M(Х), D(Х).

n = 7; p = 0,5; s = 2; k = 8.

Решение.

Случайная величина Х, очевидно, принимает значения 0, 2, 4, ... 2n.

При этом, вероятность события Х = 0 («герб» ни разу не выпал):

Вероятность события Х = 2 («герб» выпал 1 раз)

Продолжая эти рассуждения дальше, получим:

Ряд ее распределения имеет вид:

Х	0	2	4	6	8	10	12	14
Р

Как видно, условие нормировки выполняется.

а)

б) Событие «не более 8 очков» является суммой событий Х = 0, Х = 2,

Х = 4, Х = 6 и Х = 8:

в) Вероятность события Х = 8 («максимальное число очков»):

г) Вероятность события Х = 0 («минимальное число очков»):

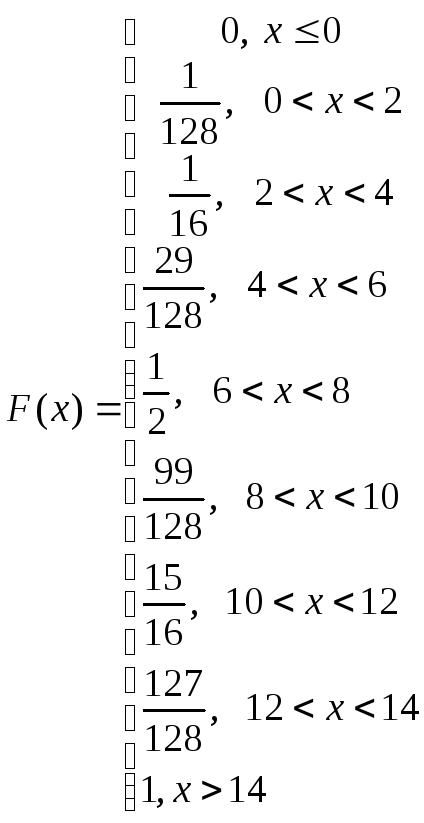
Математическое ожидание:

Дисперсия:

Задача 7.

Два стрелка поочередно стреляют по мишени до первого попадания. Вероятность промаха для первого стрелка равна р₁, для второго – р₂. На обоих было выдано n патронов. Составить ряд распределения случайной величины Х – числа израсходованных патронов. Найти M(Х), D(Х).

n = 8; p₁ = 0,1; p₂ = 0,3.

Решение.

Случайная величина Х, очевидно, принимает значения 1, 2, ... n.

При этом, событие Х = 1 («израсходован 1 патрон»), означает попадание у первого стрелка при первом выстреле. Его вероятность:

События Х = 2 («израсходовано 2 патрона») означает промах у первого стрелка и попадание у второго стрелка при первом выстреле. Его вероятность:

Продолжая эти рассуждения дальше, получим:

Однако, событие Х = 8 означает промахи обоих стрелков в предыдущих выстрелах. Поэтому вероятность этого события:

Ряд ее распределения имеет вид:

Х	1	2	3	4	5	6	7	8
Р	0,9	0,07	0,027	0,0021	0,00081	0,000063	0,0000243	0,0000027

Как видно, условие нормировки выполняется.

Математическое ожидание:

Дисперсия

Задача 8.

Книга издана тиражом n экземпляров. Вероятность того, что книга сброшюрована неправильно, равна р. Найти вероятность того, что тираж содержит:

а) ровно k бракованных книг;

б) не более k бракованных книг;

в) ни одна книга не бракована;

г) хотя бы одна книга сброшюрована неправильно.

Найти; M(Х), D(Х), где случайная величина Х – число бракованных книг.

n = 1000; p = 0,005; k = 3.

Решение.

а) Для данного условия: n = 1000; p = 0,005; q = 1 – p = 0,995.

Данные числа удовлетворяют условиям локальной теоремы Муавра-Лапласа, поэтому используем формулу Муавра-Лапласа:

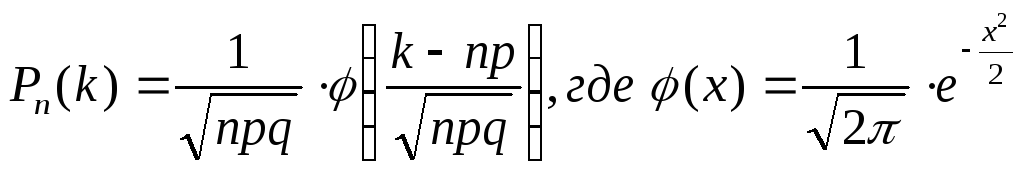при k = 3.

б) Воспользуемся интегральной формулой Муавра-Лапласа:

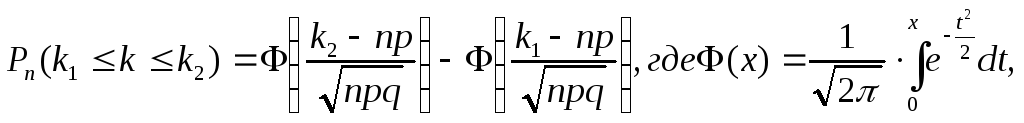
k₁ = 0 и k₂ = 3.

= 0,172.

в)

г) Событие «хотя бы одна книга сброшюрована неправильно» противоположно событию «ни одна книга не бракована», поэтому его вероятность равна:

Поскольку случайна величина Х распределена биномиально, то

Задача 9.

Случайная величина Х задана функцией распределения F(х). Требуется найти:

а) плотность распределения f(x);

б) математическое ожидание М(Х);

в) дисперсию D(Х);

г) вероятность попадания случайной величины Х на заданный интервал (α;β);

д) построить график функции f(x); F(х).

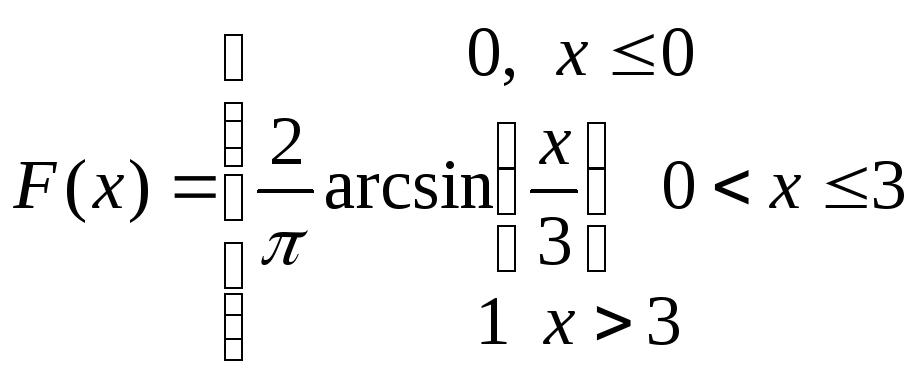α = 0; β = 3/2.

Решение.

а) Плотность распределения:

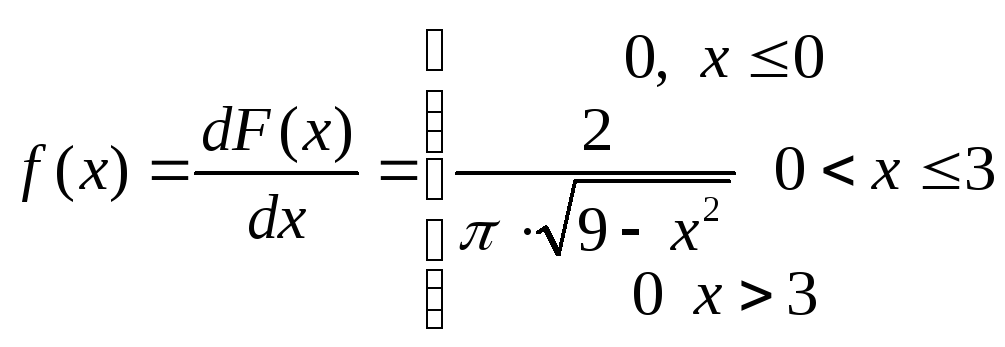
б) Математическое ожидание:

в) Дисперсия:

г)

д)

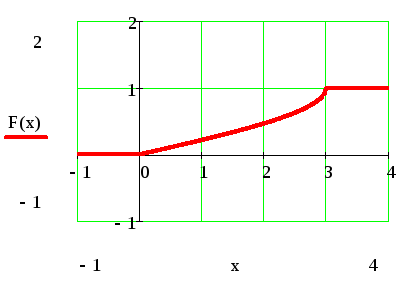
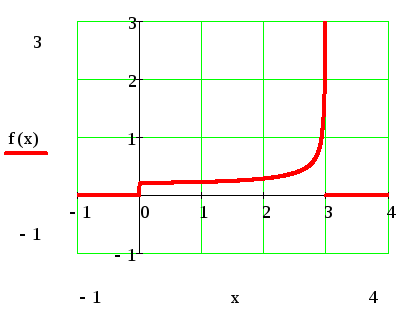
Задача 10.

Дана плотность f(x) распределения вероятностей случайной величины Х. Найти:

а) значение постоянного параметра этого распределения;

б) функцию распределения F(х);

в) математическое ожидание М(Х);

г) дисперсию D(Х);

д) вероятность попадания случайной величины Х на заданный интервал (α;β);

е) построить график функции f(x); F(х).

α = 0; β = 1/5.

Решение.

а) Найдем значение постоянного параметра распределения. Поскольку плотность распределения должна соответствовать условию нормировки

то

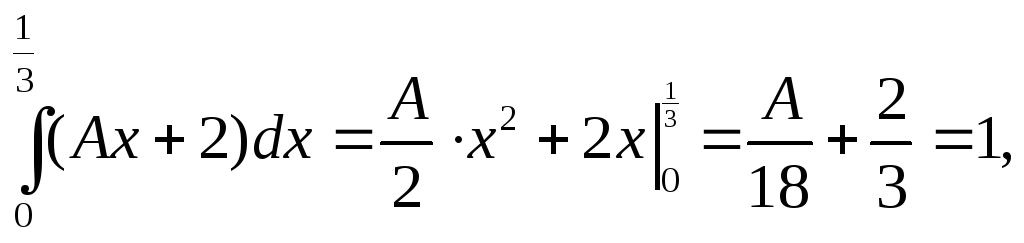откуда А = 6.

б) Поскольку то

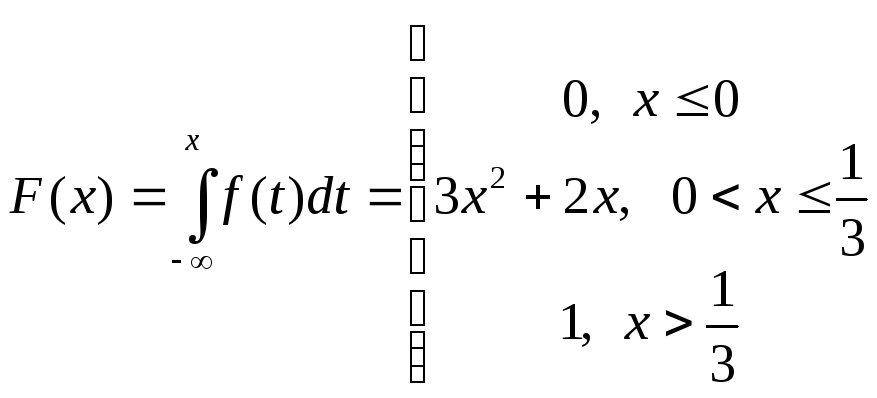
в) Математическое ожидание:

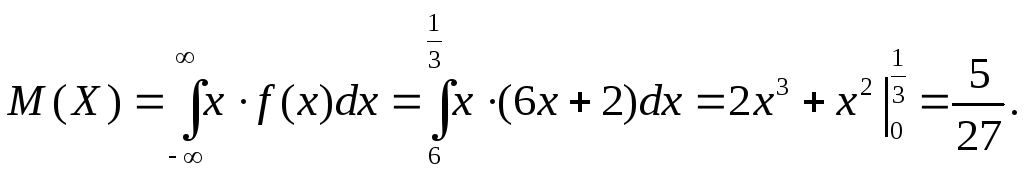г) Дисперсия:

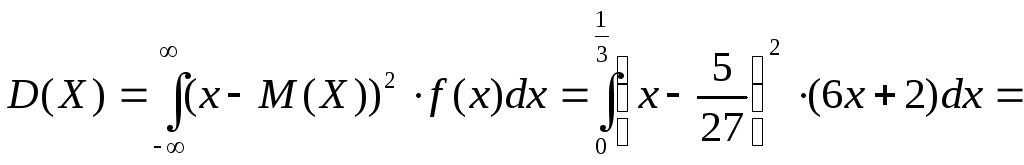
д) е)

е)

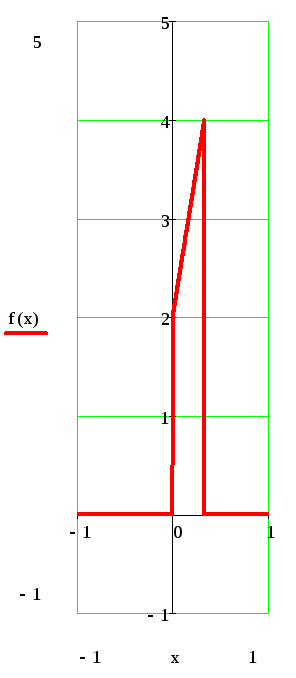
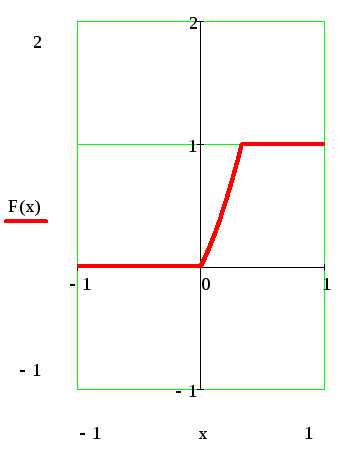
Задача 11.

Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением σ мг и математическим ожиданием 0 мг. Найти:

а) вероятность того, что взвешивание будет проведено с ошибкой, не превышающей по абсолютной величине δ мг;

б) вероятность того, что при n независимых взвешиваниях погрешность хотя бы в одном взвешивании не превосходит по абсолютной величине δ мг;

в) интервал, в котором с вероятностью 0,9973 будет заключена ошибка взвешивания.

σ = 100; δ = 1; n = 3.

Решение.

а) Для нормального распределения:

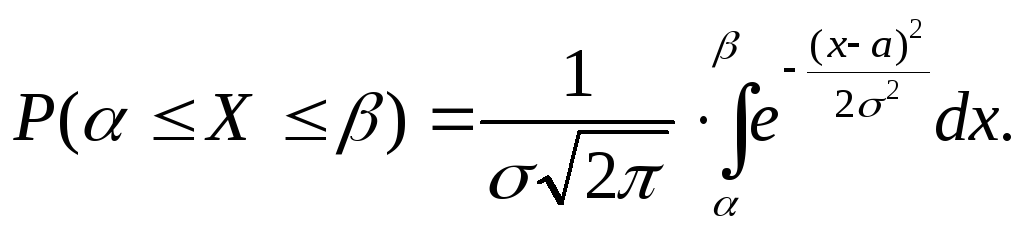
В нашем случае:

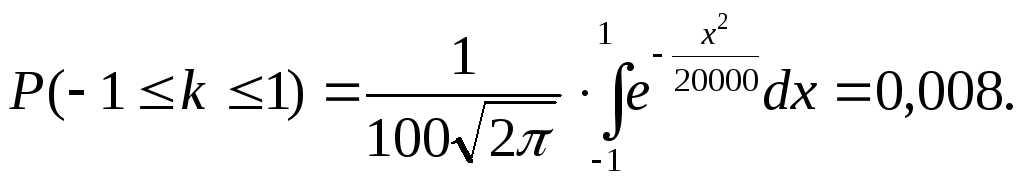
б) Событие «погрешность хотя бы в одном взвешивании не превосходит по абсолютной величине δ» противоположно событию «погрешность во всех взвешиваниях превосходит по абсолютной величине δ».

Его вероятность:

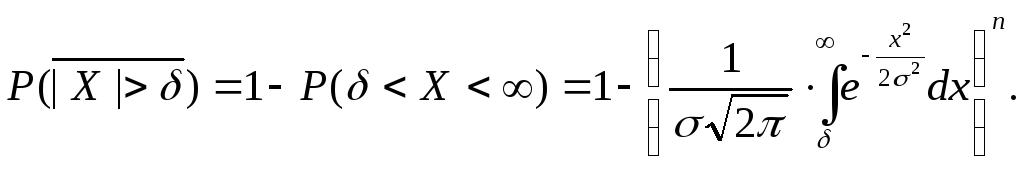
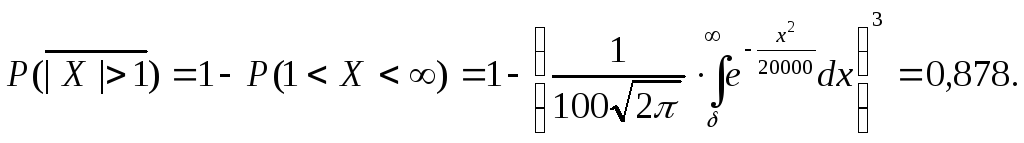
в) Имеем:

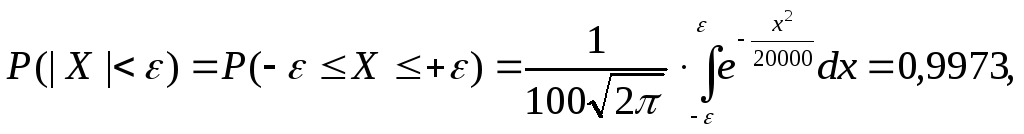
откуда ε = 300.