
Лабораторная работа № 17
Исследование затухающих электрических колебаний в колебательном контуре
Приборы и принадлежности:блок колебательного контура, осциллограф, генератор импуль-сов, магазин сопротивлений, набор конденсаторов и катушек индуктивности.
Цель работы:1.Изучение зависимости периода собственных колебаний от величинLиC.
2. Определение добротности и логарифмического декремента затухания.
3. Исследование влияния Rна затухание колебаний и добротность контура
Краткая теория
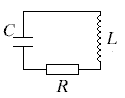
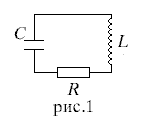 Замкнутая
цепь, состоящая из емкостиC,
индуктивностиLи активного
сопротивленияR, образует
колебательный контур(рис.1). сопротивлениеRв большинстве случаев
распределено между витками катушки
индуктивности, между контактами, в
соединительных проводах, а иногда и в
конденсаторах. При относительно невысоких
частотахR,LиCможно считать
сосредоточенными в определенных
участках цепи. Такие колебательные
контуры называются колебательными
системами с сосредоточенными постоянными.
Замкнутая
цепь, состоящая из емкостиC,
индуктивностиLи активного
сопротивленияR, образует
колебательный контур(рис.1). сопротивлениеRв большинстве случаев
распределено между витками катушки
индуктивности, между контактами, в
соединительных проводах, а иногда и в
конденсаторах. При относительно невысоких
частотахR,LиCможно считать
сосредоточенными в определенных
участках цепи. Такие колебательные
контуры называются колебательными
системами с сосредоточенными постоянными.
Данная работа посвящена исследованию различных колебательных процессов и измерению основных параметров колебательного контура.
Рассмотрим контур,
состоящий из последовательно соединенных
R,LиC.
Пусть в начальный момент конденсатор
заряжен до разности потенциаловU![]() ,
а ток в контуре равен нулю. В этот момент
вся энергия колебательного контура
сосредоточена в конденсаторе, который
начинает разряжаться, через катушку и
активное сопротивление потечет ток.
Электрическая энергия конденсатора
начнет превращаться в магнитную энергию
катушки индуктивности. Этот процесс
закончится, когда заряд конденсатора
обратится в нуль, а ток в контуре достигнет
максимума. Начиная с этого момента ток,
не меняя направления, начинает убывать.
Однако он не сразу упадет до нуля, т.к.
этому препятствует ЭДС самоиндукции.
Ток будет перезаряжать конденсатор и
вновь возникшее электрическое поле
будет ослаблять ток. В конце концов ток
обратится в нуль, а заряд (напряжение)
на конденсаторе достигнет некоторого
максимального значения, но по абсолютной
величине меньшего, чем в исходном
состоянии, т.к. часть запасенной
конденсатором энергии выделится в виде
джоулева тепла на сопротивленииR.
Конденсатор снова начнет разряжаться
и в контуре потечет ток, но уже в
противоположном направлении: возникнут
затухающие колебания тока, напряжения
и заряда конденсатора.
,
а ток в контуре равен нулю. В этот момент
вся энергия колебательного контура
сосредоточена в конденсаторе, который
начинает разряжаться, через катушку и
активное сопротивление потечет ток.
Электрическая энергия конденсатора
начнет превращаться в магнитную энергию
катушки индуктивности. Этот процесс
закончится, когда заряд конденсатора
обратится в нуль, а ток в контуре достигнет
максимума. Начиная с этого момента ток,
не меняя направления, начинает убывать.
Однако он не сразу упадет до нуля, т.к.
этому препятствует ЭДС самоиндукции.
Ток будет перезаряжать конденсатор и
вновь возникшее электрическое поле
будет ослаблять ток. В конце концов ток
обратится в нуль, а заряд (напряжение)
на конденсаторе достигнет некоторого
максимального значения, но по абсолютной
величине меньшего, чем в исходном
состоянии, т.к. часть запасенной
конденсатором энергии выделится в виде
джоулева тепла на сопротивленииR.
Конденсатор снова начнет разряжаться
и в контуре потечет ток, но уже в
противоположном направлении: возникнут
затухающие колебания тока, напряжения
и заряда конденсатора.
Затухающие колебания напряжения на конденсаторе и тока в контуре сопровождаются процессами превращения энергии электрического поля в энергию магнитного поля и обратно. Таким образом в контуре возникнут и затухающие электромагнитные колебания, которые также условно называют просто электрическими. Электрические колебания, происходящие в колебательном контуре без воздействия внешних ЭДС, называют свободными или собственными электрическими колебаниями.
Однако в зависимости от величины R,LиCразряд конденсатора в контуре может носить различный характер, который можно исследовать аналитически.
Уравнение колебательного контура получим, исходя из того, что сумма падений напряжений на индуктивности, активном сопротивлении и емкости в любой момент времени равняется нулю(2-й закон Кирхгофа).
![]() L
L![]() +iR+
+iR+
![]() = 0. (1)
= 0. (1)
Учитывая, что i=![]() иq=CU,
преобразуем соотношение (1):
иq=CU,
преобразуем соотношение (1):
![]()
![]() (2)
(2)
Вводя
обозначение
![]() (коэффициент затухания) и
(коэффициент затухания) и![]() (циклическая частота собственных
колебаний контура), уравнение (2) примет
вид:
(циклическая частота собственных
колебаний контура), уравнение (2) примет
вид:
![]()
![]() .
(3)
.
(3)
Решение
этого однородного дифференциального
уравнения второго порядка зависит от
соотношения постоянных коэффициентов
![]() и
и![]() .
.
СЛУЧАЙ
1: При условии, что![]() (затухание в контуре мало), решение
уравнения (3) может быть записано в форме:
(затухание в контуре мало), решение
уравнения (3) может быть записано в форме:
![]() (4)
(4)
г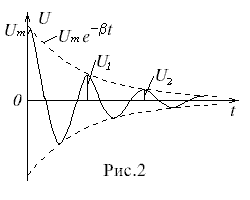 де
де![]() - частота затухающих колебаний,
- частота затухающих колебаний,
![]() - амплитуда затухающих колебаний,
- амплитуда затухающих колебаний,
![]() - начальное напряжение на конденсаторе
(приt=0).
- начальное напряжение на конденсаторе
(приt=0).
В контуре возникнут затухающие колебания, причем амплитуда колеба-ний изменятся по экспонен-циальному закону (рис. 2).
Для характеристики колебаний вводят логарифмический декремент затухания – натуральный логарифм отношения двух амплитуд(в общем случае напряжения, заряда, тока), отстоящих друг от друга по времени на один период, например:
 (5)
(5)
где
![]() - период затухающих колебаний.
- период затухающих колебаний.
Можно
показать, что
![]() ,
где
,
где![]() - число полных колебаний, совершаемых
за время, в течение которого амплитуда
уменьшается вeраз.
- число полных колебаний, совершаемых
за время, в течение которого амплитуда
уменьшается вeраз.
Колебательный
контур часто удобно охарактеризовать
его добротностью![]() ,
которая определяется как величина,
обратно пропорциональная логарифмическому
декременту затухания:
,
которая определяется как величина,
обратно пропорциональная логарифмическому
декременту затухания:
![]() .
.
![]() (6)
(6)
если
затухание очень мало(![]() ),
можно считать, что
),
можно считать, что![]() .
Тогда:
.
Тогда:
![]() ,
где
,
где![]() - характеристическое или волновое
сопротивление контура.
- характеристическое или волновое
сопротивление контура.
Можно показать, что
![]() , (7)
, (7)
где
W– энергия, запасенная
в контуре,
![]() -
энергия, рассеиваемая в контуре за один
цикл колебания.
-
энергия, рассеиваемая в контуре за один
цикл колебания.
Отсюда видно, что добротность контура характеризует его способность сохранять запасенную энергию.
Частота
![]() ,
периодT, логарифмический
декремент затухания
,
периодT, логарифмический
декремент затухания![]() ,
добротность
,
добротность![]() являются характеристическими параметрами
контура, они полностью определяются
только значениямиR,Lи С.
являются характеристическими параметрами
контура, они полностью определяются
только значениямиR,Lи С.
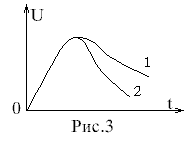
CЛУЧАЙ
2:При![]() (“потери” энергии на активном
сопротивлении велики) в контуре происходит
апериодический разряд конденсатора,
свободные колебания не возникают (рис.
3,4).
(“потери” энергии на активном
сопротивлении велики) в контуре происходит
апериодический разряд конденсатора,
свободные колебания не возникают (рис.
3,4).
 Видно,
что хотя вид графика апериодического
процесса зависит от начальных условий,
но характерным является то, чтоUасимптотически приближается к нулю приt
Видно,
что хотя вид графика апериодического
процесса зависит от начальных условий,
но характерным является то, чтоUасимптотически приближается к нулю приt![]() .
.
 Сопротивление
контура, при котором колебательный
процесс переходит в апериодический,
называется критическим. Значение
критического сопротивления
Сопротивление
контура, при котором колебательный
процесс переходит в апериодический,
называется критическим. Значение
критического сопротивления![]()
R![]() определяется из условия:
определяется из условия:
![]() ,
т.е.:
,
т.е.:
![]() .
(9)
.
(9)
