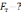Задачі фізики
.docxЗадача 1.
Матеріальна
точка здійснює прямолінійний рух (вздовж
осі Ох), кінематичне рівняння руху якої
має такий вигляд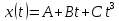 ,
де
,
де
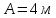 ,
,
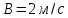 ,
,
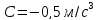 .
Визначити координату точки,
миттєву швидкість
.
Визначити координату точки,
миттєву швидкість
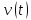 та
прискорення
та
прискорення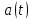 для моменту часу
для моменту часу
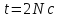 після
початку руху, де
після
початку руху, де
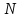 -
номер варіанту.
-
номер варіанту.
 Дано:
Дано:
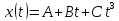
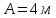
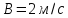
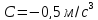
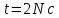

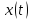
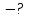
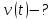
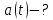
Розв’язування.
Координату
точки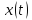 знаходимо,в рівняння руху підставляємо
час
знаходимо,в рівняння руху підставляємо
час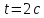 :
:
 .
.
Миттєву
швидкість
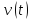 знаходимо, продиферинціювавши координату
знаходимо, продиферинціювавши координату
 за
часом
за
часом
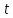 (взяти
похідну):
(взяти
похідну):
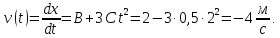 Знак мінус вказує на те, що в заданий
момент часу точка рухається в від’ємному
напрямку координатної осі Ох.
Знак мінус вказує на те, що в заданий
момент часу точка рухається в від’ємному
напрямку координатної осі Ох.
Миттєве
прискорення в довільний момент часу, знаходимо,
взявши другу похідну від координати
в довільний момент часу, знаходимо,
взявши другу похідну від координати
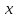 за
часом
за
часом
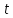 або першу похідну від швидкості за
часом
або першу похідну від швидкості за
часом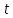 :
:
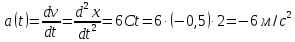 .
Знак мінус вказує на те, що в заданий
момент часу прискорення направлено в
від’ємному напрямку координатної осі
Ох.
.
Знак мінус вказує на те, що в заданий
момент часу прискорення направлено в
від’ємному напрямку координатної осі
Ох.
Відповідь: 4м, -4м/с, -6 м/с2.
Задача 2.
Матеріальна
точка здійснює обертальний рух,
кінематичне рівняння руху якої має
такий вигляд
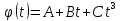 ,
де
,
де
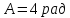 ,
,
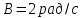 ,
,
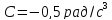 .
Визначити кутову координату точки,
миттєву кутову швидкість
.
Визначити кутову координату точки,
миттєву кутову швидкість
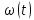 та кутове прискорення
та кутове прискорення для моменту часу
для моменту часу
 після початку руху, де
після початку руху, де
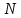 -
номер варіанту.
-
номер варіанту.
 Дано:
Дано:
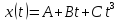
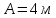
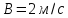

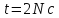

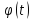
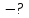
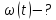
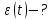
Розв’язування.
Кутову
координату точки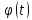 знаходимо, в рівняння руху підставляємо
час
знаходимо, в рівняння руху підставляємо
час
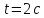 :
:
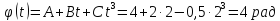 .
.
Миттєву
кутову швидкість
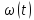 знаходимо, продиферинціювавши кутову
координату
знаходимо, продиферинціювавши кутову
координату
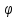 за
часом
за
часом
 (взяти
похідну):
(взяти
похідну):

Миттєве
кутове прискорення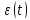 в довільний момент часу, знаходимо,
взявши другу похідну від кутової
координати
в довільний момент часу, знаходимо,
взявши другу похідну від кутової
координати
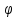 за
часом
за
часом
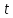 або першу похідну від кутової швидкості
за часом
або першу похідну від кутової швидкості
за часом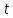 :
:
 .
.
Відповідь: 4рад, -4рад/с, -6 рад/с2.
Задача 3.
Тіло
обертається навколо нерухомої осі.
Залежність кута повороту тіла від часу
задана рівнянням
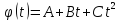 ,
де
,
де
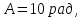
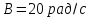 ,
,
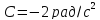 .
Знайти модуль повного прискорення точки
.
Знайти модуль повного прискорення точки
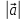 ,
розміщеної на відстані
,
розміщеної на відстані
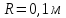 від осі обертання, в момент часу
від осі обертання, в момент часу ,
де
,
де
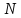 -
номер варіанту.
-
номер варіанту.
Дано:

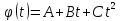
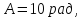
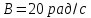
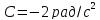
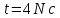


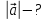
Розв’язування.
Повне
прискорення точки
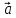 ,
яка рухається по кривій лінії, можна
знайти як геометричну суму тангенціального
прискорення
,
яка рухається по кривій лінії, можна
знайти як геометричну суму тангенціального
прискорення
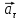 ,
направленого по дотичній до траєкторії,
та нормального прискорення
,
направленого по дотичній до траєкторії,
та нормального прискорення
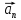 ,
направленого до центра кривизни
траєкторії:
,
направленого до центра кривизни
траєкторії:
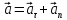 (1)
(1)
Оскільки
вектори взаємно перпендикулярні, то
модуль повного прискорення :
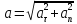 .
(2)
.
(2)
Тангенціальне та нормальне прискорення точки тіла, що обертається, виражаються за формулами:
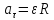 ,
,
 ,
,
де
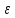 -кутове
прискорення тіла;
-кутове
прискорення тіла;
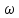 – кутова швидкість тіла.
– кутова швидкість тіла.
Замінимо
у формулі (2)
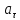 і
і
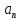 на відповідні вирази. Тоді знайдемо:
на відповідні вирази. Тоді знайдемо:
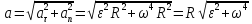 .
(3)
.
(3)
Кутову
швидкість
 обчислюємо за першою похідною від кута
повороту за часом
обчислюємо за першою похідною від кута
повороту за часом
 :
:
 .
.
Кутове
прискорення
 знаходимо, взявши першу похідну від
кутової швидкості
знаходимо, взявши першу похідну від
кутової швидкості
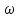 за часом
за часом
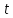 :
:
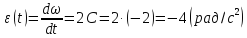 .
.
Кутове
прискорення заданого руху є сталим,
тобто не залежить від часу. Підставимо
значення
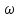 і
і
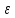 та задане значення
та задане значення
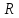 у формулу (3):
у формулу (3):
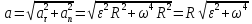 =0,1
=0,1 .
.
Відповідь: 1,65 м/с2.
Задача 4.
Матеріальна
точка масою
 рухається по колу радіусом
рухається по колу радіусом
 в площині ХОУ, причому рух її заданий
такими кінематичними рівняннями:
в площині ХОУ, причому рух її заданий
такими кінематичними рівняннями:
 ;
;
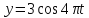 .
Визначити силу
.
Визначити силу
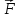 ,
яка діє на цю точку в момент часу
,
яка діє на цю точку в момент часу
 ,
де
N
–
номер варіанту.
,
де
N
–
номер варіанту.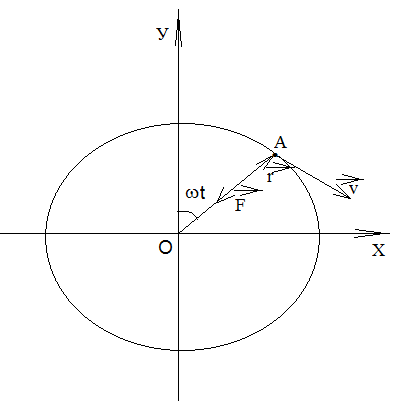
 Дано:
Дано:
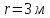
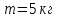
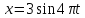
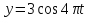
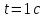


Розв’язування.
За
відомими кінематичними рівняннями руху
точки
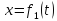 ,
,
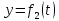 ,
,
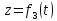 та
її масою знайти силу, що діє на точку в
будь-який момент часу.
та
її масою знайти силу, що діє на точку в
будь-який момент часу.
Розв’язок цієї задачі одержуємо безпосередньо з другого закону Ньютона в диференціальній формі. Для цього знаходимо проекції сили на осі координат:
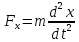 ,
,
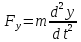 ,
,
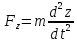 ,
за проекціями сили визначаємо модуль
сили
,
за проекціями сили визначаємо модуль
сили
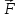 :
:
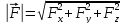 ,
а
також її напрямок у будь-який момент
часу
,
а
також її напрямок у будь-який момент
часу
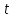 .
.
Із заданих рівнянь знаходимо проекції прискорення на осі координат:
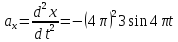 ,
,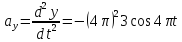 .
.
Помноживши ці рівняння на масу матеріальної точки, дістанемо проекції сили на ці осі:
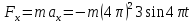 ,
,
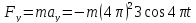 .
.
Модуль шуканої сили визначимо за формулою:
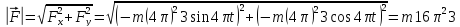 .
.
Після підстановки числових значень отримаємо:
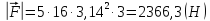 .
.
Визначимо
напрямок сили
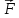 .
Для цього знайдемо напрямні косинуси:
.
Для цього знайдемо напрямні косинуси:
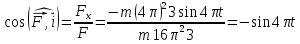 ;
;
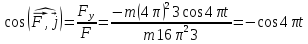 .
.
Одночасно
напрямні косинуси радіуса-вектора
 можна виразити так:
можна виразити так:
 ;
;
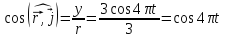 .
.
Отже,
ці вектори спрямовані по одній прямій,
але в різні боки. Тому силу визначають
за такою формулою:
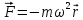 .
З цього
рівняння видно, що сила притягувальна,
оскільки її напрямок протилежний до
напрямку радіуса-вектора і вона
пропорційна масі точки та її відстані
до центра притягання, який знаходиться
в центрі кола.
.
З цього
рівняння видно, що сила притягувальна,
оскільки її напрямок протилежний до
напрямку радіуса-вектора і вона
пропорційна масі точки та її відстані
до центра притягання, який знаходиться
в центрі кола.
Відповідь: 2366,3 Н.
Задача 5.
Обчислити
дефект маси
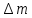 та енергію зв’язку
та енергію зв’язку
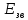 ядра
хімічного
елемента, порядковий номер
ядра
хімічного
елемента, порядковий номер
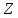 якого
збігається
із номером в списку за журналом обліку
студентів.
якого
збігається
із номером в списку за журналом обліку
студентів.
Приклад розв’язування задачі.
Обчислити
дефект маси
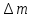 та енергію зв’язку
та енергію зв’язку
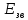 ядра
хімічного
елемента
бору
ядра
хімічного
елемента
бору
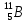 .
.
Дано:

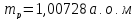
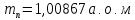
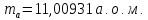
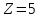

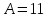
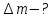

Розв'язування.
Дефект маси ядра визначають за формулою:
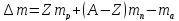 .
.
Після підстановки числових значень отримаємо:
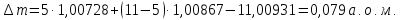
Енергія
зв’язку
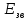 ядра визначається за формулою:
ядра визначається за формулою:
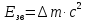 ,
,
де
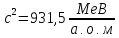 .
.
Після підстановки числових значень отримаємо:
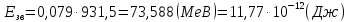 .
.
Відповідь:
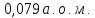 ,
,
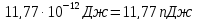 .Задача
5.
.Задача
5.
Задача 6.
Матеріальна
точка масою
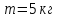 кинута з початковою швидкістю
кинута з початковою швидкістю
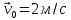 під кутом
під кутом
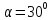 до горизонту. Знайти рух цієї точки в
просторі під дією сили земного тяжіння,
тобто визначити модуль вектора
переміщення
до горизонту. Знайти рух цієї точки в
просторі під дією сили земного тяжіння,
тобто визначити модуль вектора
переміщення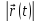 для моменту часу та знайти рівняння
траєкторії.
для моменту часу та знайти рівняння
траєкторії.
Дано:


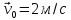
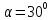

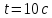

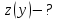
Розв'язування.
Для спрощення початкове положення тіла приймемо за початок координат системи відліку, зв’язаного з поверхнею Землі. Систему координат розмістимо так, щоб початкова швидкість знаходилась у площині YOZ, вісь Zспрямуємо вертикально вгору, а вісь У – горизонтально.
На
точку А діє лише сила земного тяжіння
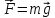 .
За такого вибору системи координат
проекції сили на осі координат
дорівнюватимуть:
.
За такого вибору системи координат
проекції сили на осі координат
дорівнюватимуть:
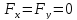 ,
,
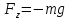 .
.
Початковими кінематичними характеристиками руху тіла будуть:
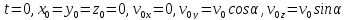 .
.
З цих умов диференціальними рівняннями руху точки є:
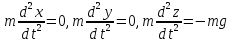 .
.
Cкоротивши
ліві і праві частини наведених рівнянь
на
 ,
дістанемо:
,
дістанемо:
 .
.
Проінтегруємо перше з цих рівнянь:
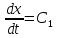 .
.
Оскільки
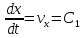 .
Тобто проекція швидкості
.
Тобто проекція швидкості
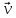 на
вісь Х є величина сталою під час руху
точки. Оскільки в початковий момент
часу
на
вісь Х є величина сталою під час руху
точки. Оскільки в початковий момент
часу
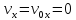 ,
то
,
то
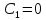 .
Врахувавши це отримаємо:
.
Врахувавши це отримаємо:
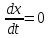 ,
звідки
,
звідки
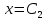 .
Для початкового моменту часу
.
Для початкового моменту часу
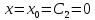 .
.
Отже,
розв’язок
першого диференціального рівняння –
це
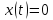 .
.
З
другого диференціального рівняння
знаходимо
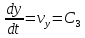 .
.
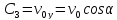 .
Проінтегрувавши останнє рівняння,
отримаємо
.
Проінтегрувавши останнє рівняння,
отримаємо
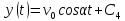 .З
початкових умов випливає, що
.З
початкових умов випливає, що
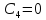 .
Тоді розв’язок
другого диференціального рівняння має
вигляд:
.
Тоді розв’язок
другого диференціального рівняння має
вигляд:
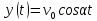 .
.
Проінтегрувавши
третє рівняння
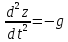 ,
дістанемо:
,
дістанемо:
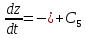 .
Константу
.
Константу
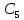 визначаємо з початкових умов. При
визначаємо з початкових умов. При
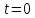 ,
,
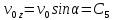 .
Отже,
.
Отже,
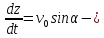 .
Проінтегруємо отримане рівняння:
.
Проінтегруємо отримане рівняння:
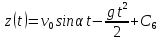 .
З
початкових умов при
.
З
початкових умов при
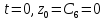 /
/
Розвязком третього диференціального рівняння є:
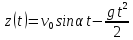 .
.
Отже, кінематичні рівняння руху точки в параметричній формі такі:
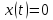 ,
,
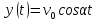 ,
,
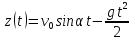 .
.
Модуль
вектора переміщення
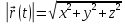 .
.
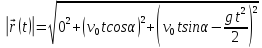
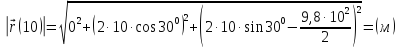
Виключивши
з цих рівнянь
параметр
 знайдемо рівняння траєкторії даної
матеріальної точки в координатах:
знайдемо рівняння траєкторії даної
матеріальної точки в координатах:
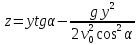 .
.
Згідно з цим рівнянням матеріальна точка, кинута під кутом до горизонту, на яку діє лише сила земного тяжіння, рухається по параболі.
Задача 7.
Людина
масою
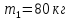 зістрибнула
з човна масою
зістрибнула
з човна масою
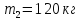 у бік, протилежний до напрямку його
руху. Швидкість руху людини відносно
води при цьому почала дорівнювати нулю.
Визначити швидкість руху човна після
того, як людина зістрибнула з нього,
якщо до цього вона становила
у бік, протилежний до напрямку його
руху. Швидкість руху людини відносно
води при цьому почала дорівнювати нулю.
Визначити швидкість руху човна після
того, як людина зістрибнула з нього,
якщо до цього вона становила
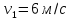 .
.
Дано:

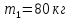

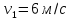
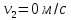


Розв'язування.
За законом збереження імпульсу
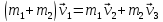 .
.
Оскільки
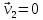 ,
то
,
то
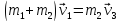 ,
звідки
,
звідки
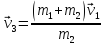 .
.
Згідно
з останнім виразом напрямок швидкості
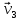 такий
самий, як і швидкості
такий
самий, як і швидкості
 .
.
Знайдемо
величину швидкості
 :
:
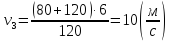 .
.
Відповідь: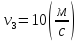 .
.
Задача 8.
Тіло
кинуто з
висоти
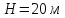 в
горизонтальному
напрямі
з
швидкістю
в
горизонтальному
напрямі
з
швидкістю
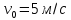 .
Визначити,
як
залежать від
часу
координати тіла
та
його повна швидкість і
визначити їх
для моменту часу
.
Визначити,
як
залежать від
часу
координати тіла
та
його повна швидкість і
визначити їх
для моменту часу
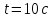 .
Вивести рівняння траєкторії.
.
Вивести рівняння траєкторії.
Дано: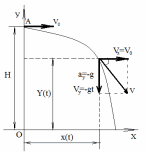

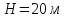
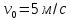

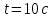

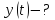
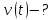
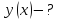
Розв'язування.
Візьмемо
систему координат ХОУ (рис.1.), початок
якої розміщений на поверхні землі, вісь
ОХ спрямована вздовж цієї поверхні в
сторону початкової швидкості, а вісь
ОУ – вертикально вгору і проходить
через точку А, з якої кинуто тіло. Рух
тіла можна уявити як суму рівномірного
руху з швидкістю
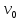 в горизонтальному напрямі і рівноприскореного
руху без початкової швидкості у
вертикальному напрямі з прискоренням
в горизонтальному напрямі і рівноприскореного
руху без початкової швидкості у
вертикальному напрямі з прискоренням
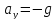 , напрямленим вниз. Складові швидкості
по осях координат у цьому разі
, напрямленим вниз. Складові швидкості
по осях координат у цьому разі
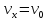 (1)
(1)
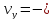 ,
(2)
,
(2)
повна швидкість
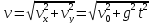 (3)
(3)
У формулу (3) підставляємо числові значення:
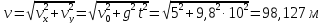 .
.
Закони руху для координат
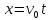 ,
(4)
,
(4)
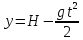 (5)
(5)
У формулу (4) і (5) підставляємо числові значення:
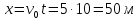 ,
,
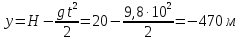 .
.
Виключивши
з виразів (4) і (5) час
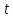 ,
дістанемо рівняння траєкторії:
,
дістанемо рівняння траєкторії:
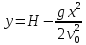 .
(6)
.
(6)
Це є рівняння параболи.
Задача 9.
Моторний човен першу половину шляху рухався по озеру зі сталою швидкістю 36км/год, а другу – зі швидкістю 18км/год. Чому дорівнює середня швидкість моторного човна на всьому шляху?
Розв’язання:
|
Дано:
|
|
|
|
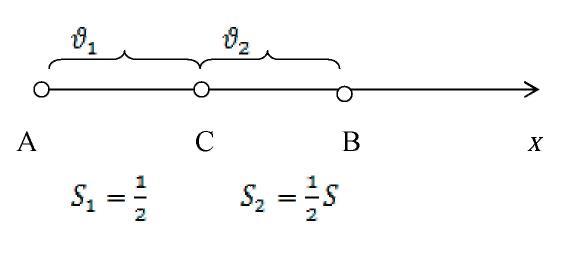
Середню
швидкість човна на всьому шляху визначимо
за формулою: 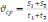
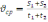
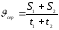 ,
для першої половини -
,
для першої половини - 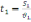
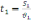 ,
для другої -
,
для другої - 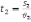
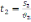 .
Підставимо значення
.
Підставимо значення 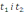
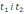 у формулу для
у формулу для 
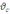 і, врахувавши
і, врахувавши 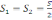
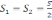 ,
отримаємо:
,
отримаємо:
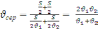
 .
.
Зробивши обчислення, отримаємо:
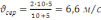
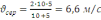 .
.
Відповідь:
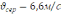
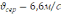 .
.
Задача 10.
Яку
силу слід прикласти, щоб рівномірно
тягнути сани вагою в 50кг, якщо мотузка
утворює з горизонтом кут 300,
а коефіцієнт тертя полозів об сніг 
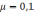 ?
?
Розв’язання:
|
Дано: m = 50кг
|
На
сани діють такі сили: сила тяги |
|
|


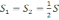
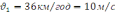
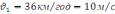
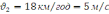

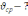
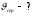
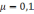

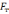
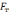 ,
напрямлена вздовж мотузки; сила тяжіння
,
напрямлена вздовж мотузки; сила тяжіння
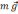
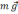 ,
напрямлена вертикально вниз; сила
тертя
,
напрямлена вертикально вниз; сила
тертя 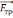
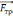 ,
напрямлена в бік
,
напрямлена в бік