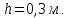Задачі з фізики для ІнМТ (Ат)

.

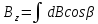З подібності трикутників ОАО’ і О’ВС випливає рівність кутів 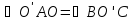(як кутів, сторони яких є взаємно перпендикулярними, 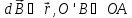). З трикутника 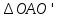випливає

.

Тоді

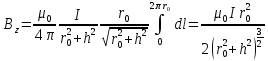. (3)

Підставивши числові значення у формулу (3), одержимо

.

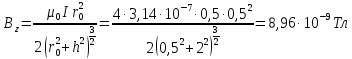Відповідь: .

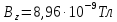Задача 9.

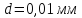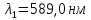Період дифракційної гратки . Яке найменше число щілин N повинна мати гратка, щоб дві складові жовтої лінії натрію і можна було бачити роздільно у спектрі першого порядку? Визначити найменшу довжину гратки.

Дано:

,

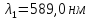
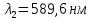
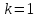
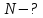Розв'язування.

Роздільна здатність дифракційної гратки визначається за формулою:

.

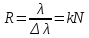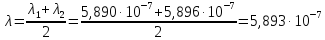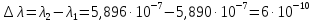(м).

(м).

Знайдемо найменше число щілин N:

.

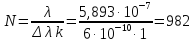Найменша довжина дифракційної гратки

.

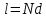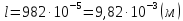
Відповідь: N=982; .

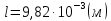Задача 10.

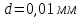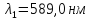Період дифракційної гратки . Яке найменше число щілин N повинна мати гратка, щоб дві складові жовтої лінії натрію і 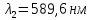можна було бачити роздільно у спектрі першого порядку? Визначити найменшу довжину гратки.

Дано:

,

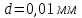
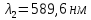
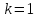
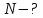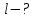
Розв'язування.

Роздільна здатність дифракційної гратки визначається за формулою:

.

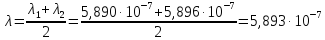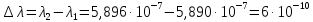(м).

(м).

Знайдемо найменше число щілин N:

.

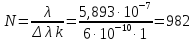Найменша довжина дифракційної гратки

.

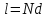Відповідь: N=982; .

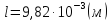Задача 11.

Плоско-випукла скляна лінза з радіусом 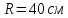дотикаэться опуклою поверхнею до скляної пластинки. При цьому у відбитому світлі радіус деякого кільця 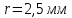. Спостерігаючи за даним кільцем, лінзу обережно відвинули від пластинки на 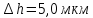. Який став радіус цього кільця.

Дано:

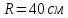
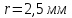
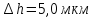
Розв'язування.

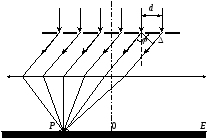
Окремим видом інтерференції світла є інтерференція в повітряному зазорі у вигляді клина між опуклою стороною плоско опуклої лінзи і поверхнею плоскої пластинки (рис. 1).

Рис. 1

Промені 1 і 2 одержані з одного променя, а тому є когерентні. Оптична різниця ходу променів у повітряному зазорі дорівнює

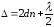, (1)

де n – показник заломлення середовища між лінзою і плоско паралельною пластинкою;

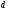– товщина зазору в указаному місці.

Промені 1 і 2 є відбитими, тому розглядається результат інтерференції у відбитому світлі. Аналогічно можна розглянути інтерференцію світла у прохідному світлі. В цьому випадку фаза поміняється на протилежну, а різниця ходу на .

Знайдемо радіуси світлих і темних кілець Ньютона у відбитому світлі.

Для світлих кілец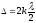ь , а для темних кілець 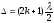, де

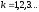
Радіус k-го кільця визначаємо з рисунка, де розглядаємо прямокутний трикутник.

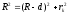, (2)

або

.

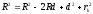Нехтуючи нескінченно малою величиною 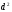, одержимо

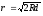. (3)

Коли лінзу обережно відвинули від пластинки на 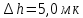, то змінилася оптична різниця ходу, що вплинуло на радіус кільця.

Радіус k-го кільця визначаємо визначаємо за формулою (3):

. (4)

З формули (3) .

Тоді

(5)

Підставляємо числові значення:

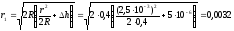(м).

.

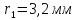Відповідь : .

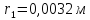Задача 12.

Молекулярний лазер безперервної дії на з газодинамічним способом збудження випромінює інфрачервоне світло потужністю 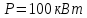. Площа перерізу лазерного пучка 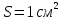. Визначити, на яку глибину можна «висвердлити» отвір у сталевій плиті за час ) (N – номер варіанту), температура якої 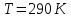, к.к.д. використання енергії становить .

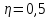Дано:

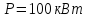
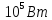
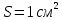
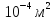
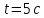
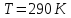
Розв'язування.

Якщо лазерний пучок випромінювання спрямувати перпендикулярно до поверхні сталевої плити, то відбуватимуться процеси нагрівання, плавлення і випаровування сталі. Діаметр отвору дорівнюватиме діаметру лазерного пучка. Для спрощення вважатимемо, що сталь, об’єм якої 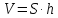(де – площа перерізу висвердленого отвору, 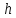- його глибина), спочатку нагрівається, а потім плавиться, к.к.д. враховує розсіяння енергії на нагрівання сталевої плити, теплопередачу і випаровування сталі в глибині ямки.

На основі рівняння теплового балансу:

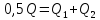, (1)

де 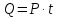– енергія. Яка передається через площу 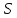за час ;

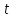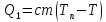– кількість теплоти, яку потрібно затратити для нагрівання сталевого тіла об’ємом від початкової температури 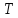до температури плавлення ; с - питома теплоємність сталі;

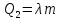– кількість теплоти, яку потрібно затратити, щоб розплавити сталеве тіло об’ємом ; 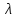– питома теплота плавлення сталі.

З врахуванням цього рівняння (1) набуває такого вигляду:

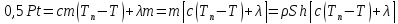, (2)

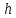- глибина просвердленого отвору; 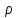– густина сталі.

З виразу (2) знайдемо

.

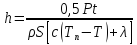Після підстановки числових значень отримаємо шукану глибину отвору :

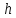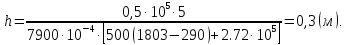
Відповідь: