§13. Уравнение плоскости

В декартовых координатах каждая плоскость определяется уравнением первой степени относительно неизвестных х, у и zи каждое уравнение первой степени с тремя неизвестными определяет плоскость.

Возьмем произвольный вектор с началом в точке. Выведем уравнение геометрического места точек М(x,y,z), для каждой из которых векторперпендикулярен вектору. Запишем условие перпендикулярности векторов:

(13.1)

Полученное уравнение линейное относительно x,y,z, следовательно, оно определяет плоскость, проходящую через точкуперпендикулярно вектору. Векторназывают нормальным вектором плоскости. Раскрывая скобки в полученном уравнении плоскости и обозначая числобуквойD, представим его в виде:

Ax+By+Cz+D= 0. (13.2)

Это уравнение называют общим уравнением плоскости. А, В, С иD– коэффициенты уравнения, А²+ В²+ С²0.

1. Неполные уравнения плоскости.

Если в общем уравнении плоскости один, два или три коэффициента равны нулю, то уравнение плоскости называют неполным. Могут представиться следующие случаи:

1) D= 0 – плоскость проходит через начало координат;

2) А = 0 – плоскость параллельна оси Ох;

3) В = 0 – плоскость параллельна оси Оу;

4) С = 0 – плоскость параллельна оси Оz;

5) А = В = 0 – плоскость параллельна плоскости ХОY;

6) А = С = 0 – плоскость параллельна плоскости ХОZ;

7) В = С = 0 – плоскость параллельна плоскости YOZ;

8) А = D= 0 – плоскость проходит через ось Ох;

9) В = D= 0 – плоскость проходит через ось Оу;

10) С = D= 0 – плоскость проходит через ось Оz;

11) А = В = D= 0 – плоскость совпадает с плоскостьюXOY;

12) А = С = D= 0 – плоскость совпадает с плоскостьюXOZ;

13) С = В = D= 0 – плоскость совпадает с плоскостьюYOZ.

2. Уравнение плоскости в отрезках.

Если в общем уравнении плоскости D0, то его можно преобразовать к виду

, (13.3)

которое называют уравнением плоскости в отрезках. - определяют длины отрезков, отсекаемых плоскостью на координатных осях.

3. Нормальное уравнение плоскости.

Уравнение

, (13.4)

где - направляющие косинусы нормального вектора плоскости, называют нормальным уравнением плоскости. Для приведения общего уравнение плоскости к нормальному виду его надо умножить на нормирующий множитель:,

при этом знак перед корнем выбирают из условия .

Расстояние dот точкидо плоскости определяют по формуле:.

4. Уравнение плоскости, проходящей через три точки

.

Возьмем произвольную точку плоскости М(x,y,z) и соединим точку М₁с каждой из трех оставшихся. Получим три вектора. Для того, чтобы три вектора принадлежали одной плоскости, необходимо и достаточно, чтобы они были компланарны. Условием компланарности трех векторов служит равенство нулю их смешанного произведения, то есть.

Записывая это равенство через координаты точек, получим искомое уравнение:

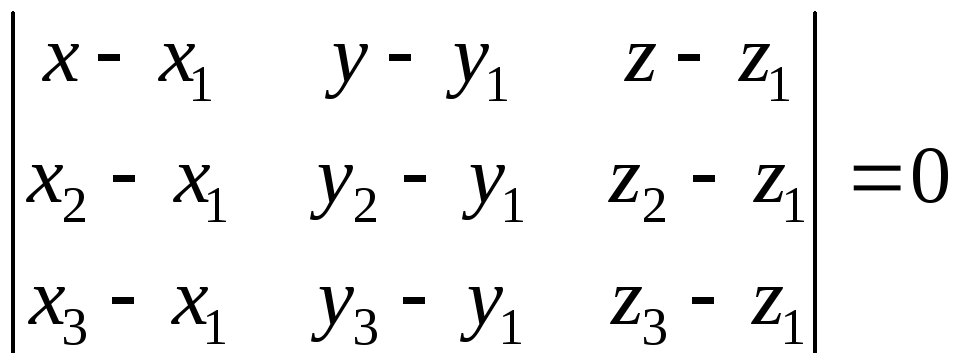. (13.5)

5. Угол между плоскостями.

Плоскости могут быть параллельны, совпадать или пересекаться, образуя двугранный угол. Пусть две плоскости заданы общими уравнениямии. Чтобы плоскости совпадали, нужно, чтобы координаты любой точки, удовлетворяющей первому уравнению, удовлетворяли бы и второму уравнению.

Это будет иметь место, если .

Если , то плоскости параллельны.

Угол , образованный двумя пересекающимися плоскостями, равен углу, образованному их нормальными векторами. Косинус угла между векторами определяется по формуле:

Если , то плоскости перпендикулярны.

Пример 21. Составить уравнение плоскости, которая проходит через две точкииперпендикулярно к плоскости.

Решение:

Запишем искомое уравнение в общем виде:. Так как плоскость должна проходить через точкии, то координаты точек должны удовлетворять уравнению плоскости. Подставляя координаты точеки, получаем:и.

Из условия перпендикулярности плоскостей имеем: . Векторрасположен в искомой плоскости и, следовательно, перпендикулярен нормальному вектору:.

Объединяя полученные уравнения, имеем:

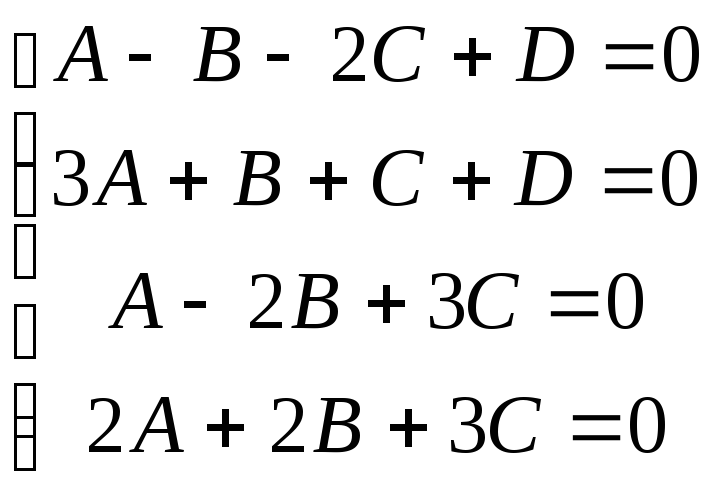
Решив систему, получим: ,,,.

Искомое уравнение имеет вид: .

Второй способ. Нормальный вектор заданной плоскости имеет координаты. Вектор. Нормальный векторискомой плоскости перпендикулярен векторуи вектору, т.е. коллинеарен векторному произведению. Вычислим векторное произведение:.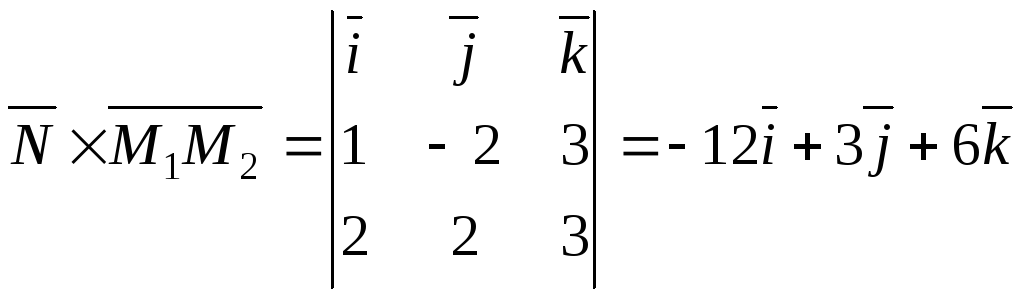

Вектор . Запишем уравнение плоскости, проходящей через точкуперпендикулярно вектору:

, илиискомое уравнение.