Архив3 / MOTsOS_kursach_ura_gotov / МОЦОС курсач ура готов / 5.расчет РЦФ

5. РАСЧЕТ РЦФ

Проектируется РЦФ нижних частот на основе аналогово-цифровой трансформации по заданным требованиям к неравномерности АЧХ.

=0.032 в полосе пропускания с частотами от 0 до =2.4 кГц, отклонение от нуля =0.022 в полосе задерживания ( от граничной частоты =4.8 кГц до ). Частота дискретизации F_d=28кГц.

Коэффициенты фильтра должны быть квантованы до m=24 разрядов (предполагается, что фильтр будет реализован (после испытаний на ПЭВМ) на базе микропроцессора DSP-56000) . Разрядность входного сигнала ЦФ должна быть 16 (что соответствует использованию 16-ти разрядного АЦП на входе сигнального микропроцессора DSP-56000).

1.Расчет нормированных «цифровых» граничных частот:

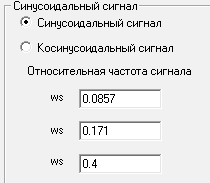
0.0857

0.171

2.Расчет значений коэффициентов затухания:

0.28дБ

33.16 дБ.

3. Расчет коэффициента билинейного преобразования:

0.0857)= 3.627

4. Определение граничной «аналоговой » частоты полосы задерживания АФ-прототипа:

= 2.16

5. Определение передаточной функции H(p) аналогового нормированного фильтра-прототипа нижних частот требуемого типа:

а) Выбираем фильтр Чебышева типа Т с равноволновыми колебаниями АЧХ в полосе пропускания и равномерным затуханием в полосе задерживания.

б) Расчет модуля коэффициента отражения по заданной величине

= 100*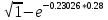=24.988%

При =10.91% выбираем из табл.1 ближайший меньший модуль коэффициента отражения, т.е =25%. соответственно =0.02803 дБ, т.е неравномерность в полосе пропускания рассчитываемого фильтра будет несколько лучше, чем требуется . Такой запас необходим, поскольку представление коэффициентов ЦФ с помощью конечного числа разрядов приводит к изменению характеристики затухания.

Таблица 1.

в) Определение вспомогательного параметра L по общей номограмме (рис.5.1.1).

Для величин =25% (=0.2803 дБ) и =33.16 дБ вспомогательный параметра L=0.08

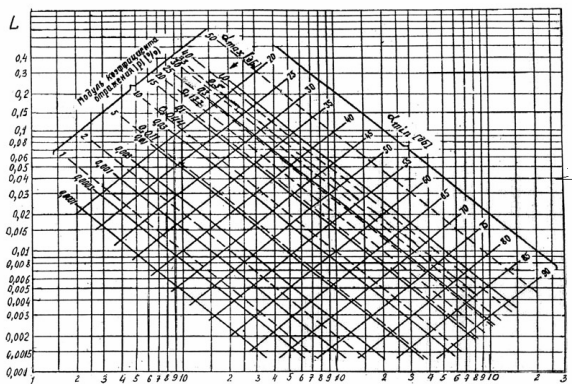
Рисунок 5.1.1

г) Определение порядка N передаточной функции АФ-прототипа по номограммам (рис.5.1.2)для фильтра Чебышева типа Т. Для величин L=0.08 и =2.16 из номограмм порядок принимаем N=4.

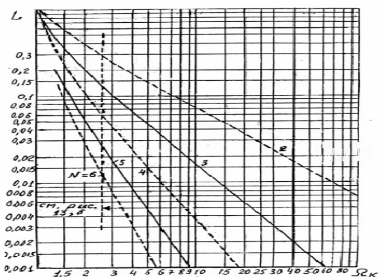
Рисунок 5.1.2

е) Запись передаточной функции H(p) в общем виде.

Для ТО (Таблица 2); и =25%

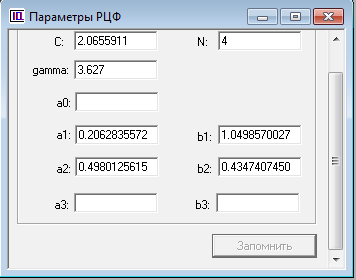
С=2.0655911

а₂=0.4980125615

b₂=0.4347407450

-а₁=0.2062835572

b₁=1.0498570027

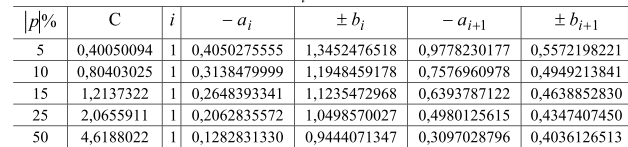
Таблица 2.

ж) Запись передаточной функции H(p) аналогового нормированного ФНЧ с численными значениями коэффициентов.

6. Расчет и построение АЧХ H() и коэффициента затухания АФ-прототипа.

А.

Б.

В.

Г.

Д.

Рис.5.1 А)АЧХА. Б) АЧХЦ В) ЛАЧХА Г) ЛАЧХЦ Д) ФЧХЦ

Системная функция H(z) цифрового фильтра нижних частот определяется с помощью подстановки

3.627*в выражение H(p):

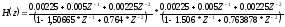
a₀=0.00225

a₁=0.005

a₂=0.00225

8. Контрольная проверка устойчивости рассчитанного РЦФ.

b₁= - 1.50665

b₂=0.764

Условие устойчивости выполняется, следовательно РЦФ устойчив.

9. Для вычисления АЧХ и ФЧХ РЦФ классическим методом переходят от системной функции H(z) к комплексному коэффициенту передачи , подставляя .

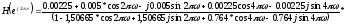
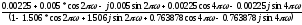
5.1 Анализ качественных характеристик РЦФ

10. Импульсная характеристика РЦФ.

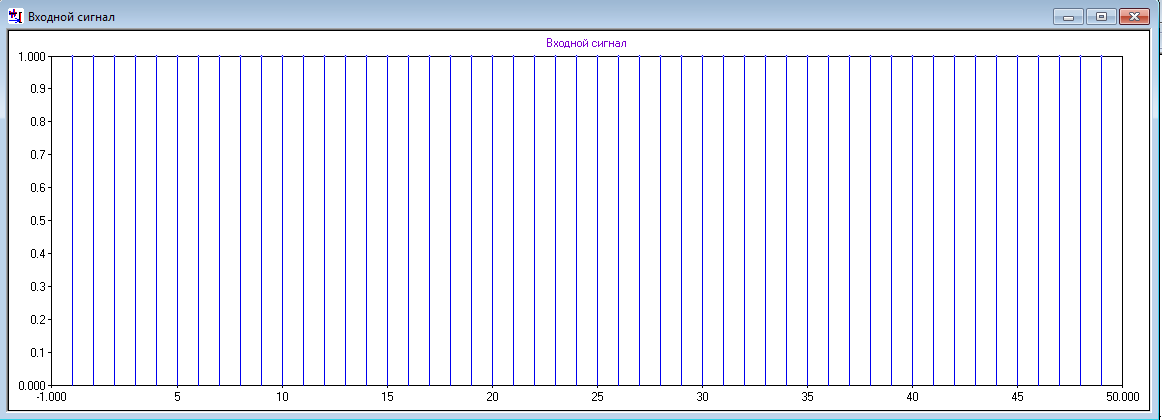
11. ЦЕдиничная последовательность.

12. Дискретизированный косинусоидальный сигнал

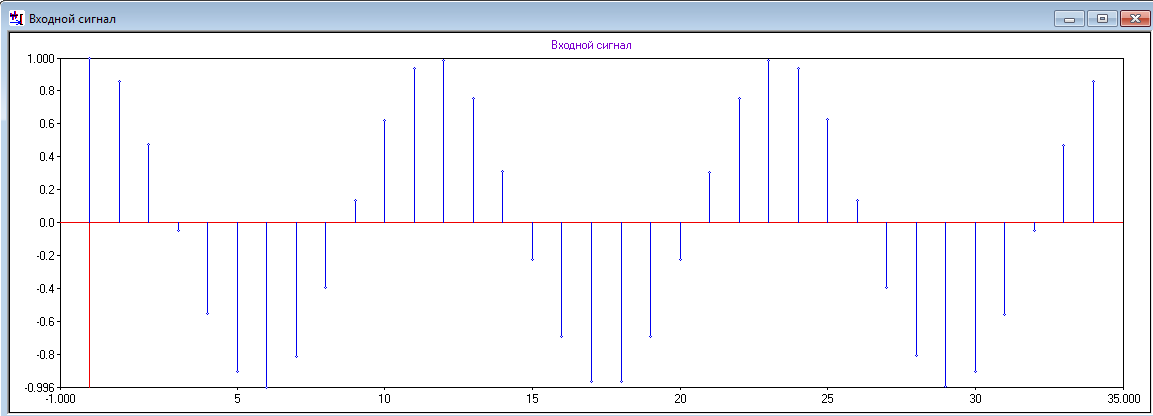
13.Дискретизированный синусоидальный сигнал.

14. Вещественный полигармонический сигнал.

Вывод: РЦФ по сравнению с НЦФ дает лучшие характеристики при маленьком порядке (N=4), за счет введение обратной связи. Но РЦФ не имеет точно линейную фазо-частотную характеристику, а также у него более высокие собственные шумы.