Верификационные примеры
ВЕРИФИКАЦИОННЫЕ ПРИМЕРЫ
Вданной главе рассмотрено решение некоторых простейших задач, имеющих аналитическое решение с целью оценки точности работы системы конечно-элементного анализа. Все приведенные здесь примеры можно найти в библиотеке файлов «Верификационные примеры».
Примеры расчётов задач статики
Изгиб консольно-защемлённой балки под действием сосредоточенной нагрузки
Рассмотрим консольно-защемлённую балку длиной L, |
P |
которая нагружена силой P на правом конце. |
|
Поперечным сечением балки является прямоугольник |
L |
с шириной b и высотой h. |
Требуется определить максимальные прогибы балки.
h
b |
Примем P=2000 Н, L=0.5 м, b=0.05 м, h=0.02 м. Характеристики материала оставим заданными по умолчанию: модуль упругости E = 2.1E+011 Па, коэффициент Пуассона v = 0.28.
Левый торец балки закрепим, а на правый приложим нагрузку величиной P, направленную вертикально вниз.
Конечно-элементная модель балки с нагрузками и закреплениями
Аналитическое решение имеет вид [1, с.215]:
w = |
Pl 3 |
=1.1905 ×10−2 м, |
|
3EJ |
|||
|
|
где P – сила, l – длина балки, E – модуль упругости материала, J = b12h3 – момент инерции сечения.
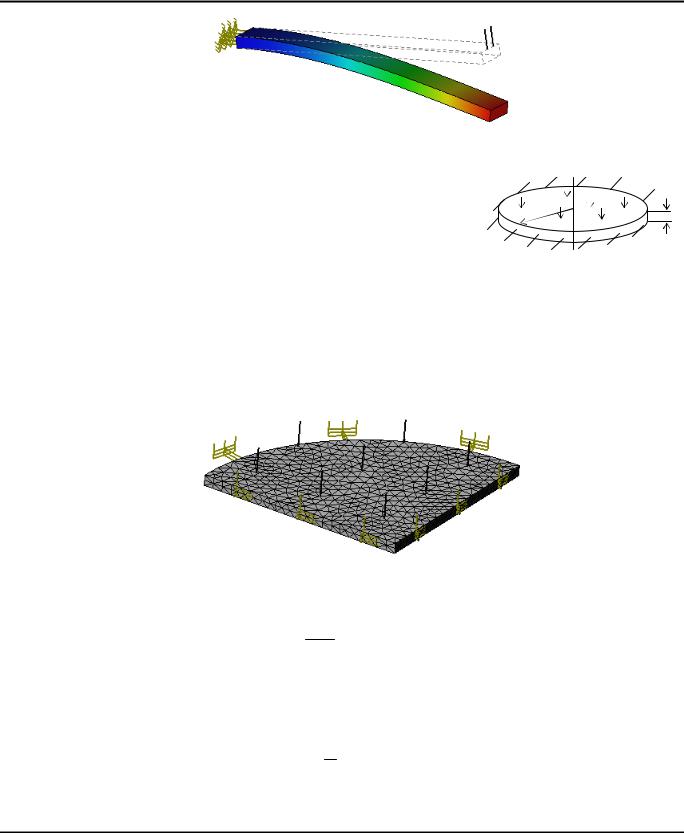
Выполнив расчет при помощи T-FLEX Анализ, получаем следующие результаты:
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1. |
||
|
|
|
|
|
|
Параметры конечно-элементной сетки |
|||||||||
|
|
|
|
|
Число конечных элементов |
|
|
||||||||
Тип конечных элементов |
|
Число узлов |
|
|
|||||||||||
|
|
|
|
|
764 |
|
|
|
|
|
|||||
квадратичный тетраэдр (10 узлов) |
|
315 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2. |
||
|
|
|
|
|
|
|
Результат «Перемещение» |
||||||||
|
|
|
|
|
|
w − w* |
|
|
|
|
|||||
Численное решение |
|
Аналитическое решение |
|
Ошибка δ = |
|
|
×100% |
|
|
||||||
Перемещение w |
* |
, м |
|
|
Перемещение w , м |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
w |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0.66 |
|
|
|
|
|
|||
1.1826E-002 |
|
|
|
|
1.1905E-002 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
179
Руководство пользователя T-FLEX Анализ
Перемещения точек балки
Статический расчет круглой пластины, защемленной по контуру
Необходимо определить максимальные прогибы круглой пластины радиуса R и толщины h, которая защемлена по контуру и нагружена равномерным давлением q, распределенным по верхней грани пластины.
q
R
h
Вследствие симметрии задачи будем рассматривать одну четвертую часть пластины.
Примем радиус пластины равным R = 0.2 м, толщину h = 0.003 м, давление q = 10 кН/м2. Характеристики материала оставим заданными по умолчанию: модуль упругости E = 2.1E+011 Па, коэффициент Пуассона v = 0.28.
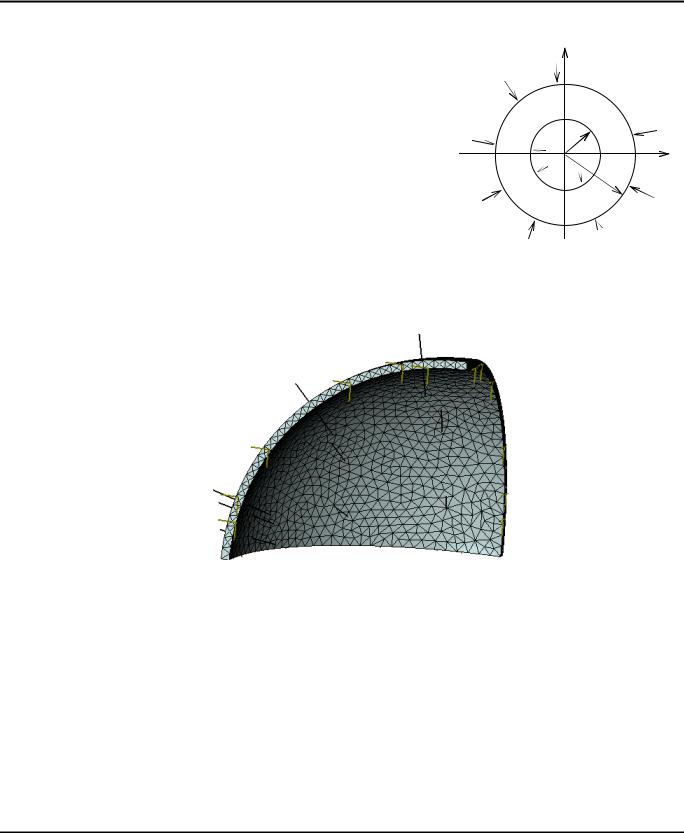
Далее необходимо наложить граничные условия. Боковую поверхность пластины закрепляем полностью, а на грани, которые оказались свободными после отбрасывания ¾ пластины, накладываем частичные ограничения по нормали к граням, так как точки этого сечения по условиям симметрии не могут получить преимущественных смещений в нормальном направлении. На верхнюю грань пластины прикладываем давление величиной 10 кН/м2.
Конечно-элементная модель пластины с нагрузками и закреплениями
Для данной задачи известно аналитическое решение. Прогиб в центре пластины вычисляется по формуле [1, с.566]:
w = qR4 = 4.8762 ×10−4 м, 64D
где |
D = |
|
Eh3 |
– изгибная жесткость, q – величина давления, R – радиус пластины. |
||
12(1 |
−ν 2 ) |
|||||
|
|
|
||||
Напряжения на контуре пластины вычисляются по формуле:
σ= 0.75q R 2 = 3.3333×107 Па .
h
180
|
|
|
|
|
|
|
|
|
|
|
|
|
Верификационные примеры |
||||||||||||||
|
Выполнив расчет при помощи T-FLEX Анализ, получаем следующие результаты: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1. |
||
|
|
|
|
|
|
|
|
|
|
|
|
Параметры конечно-элементной сетки |
|||||||||||||||
|
|
|
|
|
|
|
|
Число конечных элементов |
|
|
|||||||||||||||||
|
Тип конечных элементов |
|
Число узлов |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
11794 |
|
|
|
|
|
|
|
|
|
|||||||||
|
квадратичный тетраэдр (10 узлов) |
|
3981 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Результат «Перемещение» |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
w − w* |
|
|
|
|
|
|
|
|||||||||
|
Численное решение |
|
Аналитическое решение |
|
Ошибка δ = |
|
|
|
|
|
|
|
×100% |
|
|
||||||||||||
|
Перемещение w |
* |
, м |
|
|
Перемещение w , м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0.16 |
|
|
|
|
|
|
|
|
|
|||||||
|
4.8681E-004 |
|
|
|
|
|
4.8762E-004 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Результат «Напряжение» |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Численное решение |
|
Аналитическое решение |
|
|
|
|
|
σ −σ* |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Напряжение σ |
* |
, |
|
Н |
|
|
|
Напряжение σ , |
Н |
|
|
Ошибка δ = |
|
|
|
|
|
|
|
|
|
×100% |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
м2 |
|
|
м2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
9.83 |
|
|
|
|
|
|
|
|
|
|||||||||
|
3.0057E+007 |
|
|
|
|
|
3.3333E+007 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перемещения точек пластины
181
Руководство пользователя T-FLEX Анализ
Расчет сферического сосуда давления
Имеется сферический сосуд с внутренним радиусом r и внешним радиусом R. На сосуд действуют внутреннее давление p0 и внешнее p1. Необходимо определить перемещения внутренней стенки сосуда.
Вследствие симметрии задачи будем рассматривать одну восьмую часть сферы. Примем следующие исходные данные:
внутренний радиус r=0.4 м, внешний радиус R=0.415 м, внутреннее давление p0=200 МПа, внешнее давление p1=120 МПа.
Характеристики материала примем E = 2.1 1011 Па,ν = 0.28 .
у
p1
r
х p0 
R
Как и в предыдущей задаче, необходимо наложить граничные условия, учитывающие воздействие отброшенной части сферы. В данном случае необходимо ограничить по нормали перемещения точек всех плоских граней. На внутреннюю и внешнюю грани прикладываем давления 200 МПа и 120 МПа соответственно.
Конечно-элементная модель одной восьмой части сферы с нагрузками и закреплениями
Перемещение внутренней поверхности сферы можно рассчитать по формуле [1, с.737]:
|
|
|
|
|
|
|
|
|
|
|
|
U = A r + |
|
B |
|
|
=1.4063 мм, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
P1 |
− |
|
P0 |
|
|
|
|
|
|
|
P1 − P0 |
|
|
|
|
|
E |
|
E ν |
|
||||||
где A = |
|
r3 |
|
R3 |
|
|
|
|
|
|
, B = |
|
|
|
, |
μ = |
, λ = |
. |
||||||||||
|
|
1 |
|
1 |
|
1 |
2 (1+ν) |
(1+ν) (1− 2ν) |
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
|
(2μ +3λ) |
|
|
|
− |
|
|
|
|
4μ |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|||||
|
|
R |
3 |
r |
3 |
|
|
R |
3 |
r |
3 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В сферической системе координат выражения для напряжений имеют вид:
|
|
|
r−3P |
− R−3P |
(P |
− P ) |
ρ−3 , σ |
|
|
r |
−3P |
− R−3P |
(P |
− P ) |
ρ−3 . |
||
σ |
ρ |
(ρ) = |
1 |
0 |
− |
1 |
0 |
t |
(ρ) = |
|
1 |
0 |
+ |
1 |
0 |
||
|
|
(R−3 − r−3) |
(R−3 − r−3) |
|
|
|
(R−3 − r−3) |
2 (R−3 − r−3) |
|
||||||||
182