
- •Содержание
- •Введение
- •Технические требования
- •Требования к компьютеру
- •Рекомендуемые параметры вычислительной техники для эффективной (профессиональной) работы с T-FLEX Анализом
- •Установка системы T-FLEX Анализ
- •Структурная организация приложения T-FLEX Анализ
- •Этапы анализа конструкций
- •Быстрое начало
- •Шаг 1. Подготовка объёмной твердотельной модели изделия
- •Шаг 2. Создание «Задачи»
- •Шаг 3. Назначение материала
- •Шаг 4.1 Наложение граничных условий. Задание закреплений
- •Шаг 4.2 Наложение граничных условий. Задание нагружений
- •Шаг 5. Выполнение расчёта
- •Шаг 6. Анализ результатов расчёта
- •Подготовка конечно-элементной модели для Анализа (Препроцессор)
- •Виды конечно-элементных моделей
- •Назначение и роль сеток
- •Виды и роль граничных условий
- •Управление «Задачами», команды управления задачами
- •Общие свойства задач
- •Задание материала
- •Построение сетки
- •Параметры сетки
- •Задание ограничений
- •Полное закрепление
- •Частичное закрепление
- •Контакт
- •Упругое основание
- •Задание нагрузок
- •Механические нагрузки
- •Сила
- •Давление
- •Вращение
- •Ускорение
- •Цилиндрическая нагрузка
- •Крутящий момент
- •Осциллятор
- •Дополнительная масса
- •Тепловые нагрузки
- •Температура
- •Тепловой поток
- •Тепловая мощность
- •Конвективный теплообмен
- •Излучение
- •Сводная таблица нагрузок
- •Редактирование нагрузок и закреплений
- •Настройки и сервисные команды
- •Работа с 3D окном при подготовке элементов задач
- •Особенности работы с параметрической моделью
- •Экспорт
- •Обработка результатов (Постпроцессор)
- •Общие принципы работы с результатами
- •Настройки и сервисные команды окна результатов расчёта
- •Настройка окна результатов расчёта
- •Настройка цветовой шкалы
- •Использование датчиков для анализа результатов
- •Использование графиков для анализа результатов
- •Интегральное значение
- •Построение сечений
- •Генерация отчётов
- •Пример интерпретации результата
- •Статический анализ
- •Особенности этапов статического анализа
- •Алгоритм оценки статической прочности по результатам моделирования
- •Настройки процессора линейной и нелинейной статики
- •Задача оптимизации
- •Задача об оптимизации толщины балки
- •Приложение (справочные материалы)
- •Характеристики конструкционных материалов
- •Объёмное напряжённо-деформированное состояние в точке
- •Оценка статической прочности конструкций. Теории прочности
- •Анализ устойчивости
- •Особенности этапов анализа на устойчивость
- •Алгоритм оценки устойчивости по результатам моделирования
- •Настройки Процессора анализа устойчивости
- •Частотный анализ
- •Особенности этапов частотного анализа
- •Настройки Процессора частотного анализа
- •Вынужденные колебания
- •Вводные сведения
- •Особенности этапов анализа вынужденных колебаний
- •Настройки препроцессора анализа вынужденных колебаний
- •Настройки процессора анализа вынужденных колебаний
- •Настройки постпроцессора и анализ результатов вынужденных колебаний
- •Анализ Усталости
- •Цикл напряжений. Основные характеристики
- •Кривая усталости
- •Методы коррекции напряжений
- •Оценка характеристик сопротивления усталости при сложном напряженном состоянии
- •Этапы анализа усталости
- •Результаты усталостного расчёта
- •Примеры расчётов деталей на усталостную прочность
- •Однособытийный усталостный расчет
- •Многособытийный усталостный расчет
- •Примеры результатов однособытийного усталостного расчёта
- •Пример результатов многособытийного усталостного расчёта
- •Тепловой анализ
- •Особенности этапов теплового анализа
- •Настройки Процессора теплового анализа
- •Примеры тепловых расчётов
- •Тепловой расчёт радиатора охлаждения. Установившийся режим
- •Расчёт времени нагревания радиатора охлаждения. Нестационарный режим
- •Расчёт времени остывания радиатора охлаждения. Нестационарный режим
- •Верификационные примеры
- •Примеры расчётов задач статики
- •Изгиб консольно-защемлённой балки под действием сосредоточенной нагрузки
- •Статический расчет круглой пластины, защемленной по контуру
- •Расчет сферического сосуда давления
- •Квадратная пластина под силой в центре
- •Цилиндрический резервуар со стенками постоянной толщины
- •Кручение бруса с круглым поперечным сечением
- •Стержень под действием собственного веса
- •Расчёт вращающегося сплошного диска постоянной толщины
- •Свободно опертая прямоугольная пластинка под синусоидальной нагрузкой
- •Температурные напряжения биметаллического элемента
- •Примеры расчётов задач устойчивости
- •Расчет устойчивости сжатого прямого стержня
- •Устойчивость квадратной пластины
- •Устойчивость прямоугольной пластины
- •Примеры задач частотного анализа
- •Определение собственных частот колебаний балки
- •Определение первой собственной частоты колебаний круглой пластинки
- •Свободные колебания сферического купола
- •Примеры задач теплового анализа
- •Установившаяся температура
- •Поток тепла в шаре
- •Теплопроводность цилиндрической стенки
- •Литература
|
|
|
|
|
Анализ усталости |
Методы коррекции напряжений |
|
|
|
|
|
Пусть σ * - скорректированное знакопеременное напряжение, σT - предел текучести, σΠ - предел |
|||||
прочности, тогда: |
|
|
|
|
|
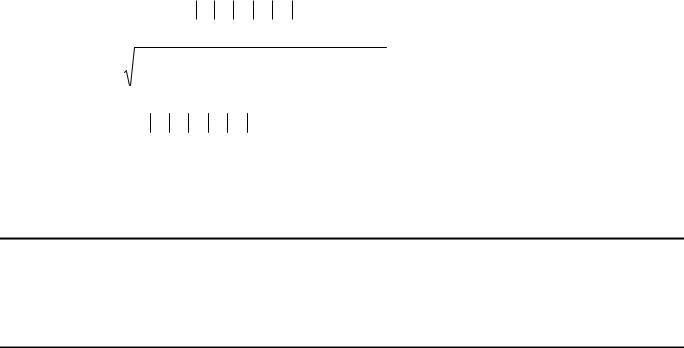
1. метод Содерберга: σ* = |
σa |
|
|
|
|
|
σ |
|
|
||
|
|
|
m |
|
|
|
|
|
|||
|
1− |
|
|
|
|
|
|
σT |
|||
2. метод Гудмэна используется для хрупких материалов: σ* = |
|
σa |
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|||||
|
|
|
|
|
m |
|
||||
|
|
|
|
|
||||||
|
1− |
|
|
|
|
|
||||
|
|
|
σΠ |
|||||||
3. метод Гербера используется для пластичных материалов:σ* = |
|
|
|
σa |
|
|
|
|||
|
|
|
σ |
m |
2 |
|||||
|
|
|
|
|||||||
|
1− |
|
|
|
|
|||||
|
|
|
|
|||||||
|
|
σ |
|
|
|
|||||
|
|
|
|
|
Π |
|||||
Оценка характеристик сопротивления усталости при сложном напряженном состоянии
Условия прочности при переменных напряжениях в целом аналогичны условиям прочности статического анализа, но в качестве предельного допускаемого напряжения используется предел
усталости σR . Соответственно, гипотезы проверки усталостной прочности по критерию недопущения пластических деформаций в усталостном расчете принимают вид σ* ≤σR . Напомним
общие выражения традиционных гипотез проверки прочности (по условию пластичности), используемых для оценки прочности конструкций:
1. Гипотеза Треска – Сен-Венана (гипотеза максимальных касательных напряжений)
σT < (σ1 −σ3 ) , σ1 ≥ σ2 ≥ σ3 ;
2. Гипотеза Губера – Мизеса – Генки (гипотеза энергии формоизменения)
σT < |
1 |
((σ1 −σ2 )2 |
+ (σ2 −σ3 )2 + (σ1 −σ3 )2 ); |
|
2 |
||||
|
|
|
3. Гипотеза Геста – Мора (гипотеза наибольших главных напряжений)
σT <σ1 , σ1 ≥ σ2 ≥ σ3 ,
где σT - предел текучести, σ1 ,σ2 ,σ3 - главные напряжения.
Поэтому при анализе усталости мы также получаем три варианта коэффициента запаса, соответствующих каждой из общепринятых теорий проверки прочности.
Этапы анализа усталости
Перед выполнением расчёта на усталостную прочность, необходимо сначала исследовать действие статической нагрузки на рассматриваемую деталь или конструкцию (т.е. выполнить статический анализ). Это необходимо для того, чтобы выяснить, подвергается ли изделие разрушению под действием заданной нагрузки. Если изделие разрушается при заданном статическом нагружении (коэффициент запаса меньше 1), то выполнять Анализ усталости не имеет смысла.
143

Руководство пользователя T-FLEX Анализ
Предварительный расчёт задачи статического анализа необходим еще и потому, что рассчитанные в статическом анализе напряжения (эквивалентные или главные) будут использованы для расчёта усталостной прочности в качестве амплитуды циклических напряжений.
Кроме того при расчёте усталости необходимо, чтобы для материала, из которого изготовлено рассматриваемое изделие, была определена кривая усталости.
Кривая усталости может быть выбрана из уже существующих кривых, или задана самостоятельно. При помощи команды:
Клавиатура |
Текстовое меню |
Пиктограмма |
|
|
|
<PL> |
«Параметры|Графики» |
|
|
|
|
можно вызвать диалог для работы с кривыми усталости. Таким образом, пользователь может создавать новые, редактировать или удалять уже существующие кривые.
Вид кривой (ломаная или гладкая кривая) определяется при создании графика.
144

Анализ усталости
После того как кривая создана (определен её тип и имя), необходимо задать узлы кривой и значения функции в них.
Ломаная
Гладкая кривая
145

Руководство пользователя T-FLEX Анализ
Полностью заданная кривая усталости имеет следующий вид:
График кривой можно сохранить во внешний файл для того, чтобы в дальнейшем его можно было повторно использовать в других усталостных расчётах.
Далее необходимо выполнить привязку кривой усталости к материалу задачи. Для этого выберете тело, при помощи контекстного меню необходимо вызвать диалог «Свойства тела» (команда «Свойства»), перейти в диалоговое окно «Материалы» (при помощи кнопки «Материалы»). В диалоге «Материалы» из списка «Текущая модель» выбрать нужный материал и нажать кнопку «Дополнительно». В появившемся диалоге «Свойства материала» для параметра «Закон усталости» выбрать кривую усталости.
146

Анализ усталости
Если 3D модель является сборкой, т.е. состоит из 3D фрагментов, то для того, чтобы привязать кривую усталости к материалу фрагмента необходимо в дереве задач выбрать 3D фрагмент, затем при помощи контекстного меню вызвать диалог «Параметры 3D фрагмента» (команда «Свойства»), выключить опцию «Атрибуты с исходной операции», перейти в диалоговое окно «Материалы» (при помощи кнопки «Материалы»).
В диалоге «Материалы» из списка «Текущая модель» выбрать нужный материал и нажать кнопку «Дополнительно». В появившемся диалоге «Свойства материала» для параметра «Закон усталости» выбрать кривую усталости.
Далее создадим задачу Анализа усталости. Задача создается при помощи команды:
Клавиатура |
Текстовое меню |
|
Пиктограмма |
|
|
|
|
<3MN> |
«Анализ|Новая задача|Конечно- |
|
|
элементный анализ» |
|
|
|
|
|
|
Для осуществления усталостного расчёта при создании задачи пользователь указывает её тип – «Анализ усталости» - в окне свойств команды.
После создания задачи типа «Анализ усталости» необходимо создать в ней одно или несколько событий при помощи команды:
Клавиатура |
Текстовое меню |
|
Пиктограмма |
||
|
|
|
|
|
|
<3CE> |
«Анализ|Создать событие» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В однособытийном расчёте предполагается, что все нагрузки, приложенные к системе, циклически изменяются по одному закону (параметры количество циклов и тип циклического изменения для всех нагружений одинаковы). Многособытийный расчёт позволяет оценить воздействие нескольких сил с разными параметрами циклического нагружения (разное количество циклов или несовпадающие типы изменения циклического нагружения). Каждое событие добавляется в папку «События» в дереве задачи.
147

Руководство пользователя T-FLEX Анализ
Отметим, что для возможности осуществить многособытийный расчёт усталости, необходимо, чтобы конечно-элементные сетки всех задач статики, входящих в усталостный расчёт, совпадали, и одно и то же тело каждой задачи статики состояло из одного и того же материала.
Затем необходимо добавить рассчитанную задачу статики и задать параметры циклического нагружения: количество циклов, тип нагружения, метод коррекции напряжений (задается в том случае, если коэффициент асимметрии цикла R не совпадает с коэффициентом заданной кривой усталости), коэффициент масштабного эффекта (коэффициент масштабирования напряжений). Также в диалоге «Параметры задачи (анализ усталости)» на вкладке «Цикличность» можно задать коэффициент местной концентрации напряжений (по умолчанию, коэффициент равен 1).
148
