Анализ устойчивости

Особенности этапов анализа на устойчивость

Анализ на устойчивость осуществляется в несколько этапов. Последовательность действий пользователя по подготовке задачи и выполнению расчёта конструкции на устойчивость во многом схожа с алгоритмом, описанным для Статического анализа. Поэтому в данной главе отметим только некоторые особенности, характерные для расчёта на устойчивость:

1.Создание задачи. При создании задачи нужно указать её тип – «Анализ устойчивости»

2.Наложение граничных условий. В анализе устойчивости, как и в статическом анализе, роль граничных условий выполняют закрепления и нагрузки. При анализе на устойчивость могут использоваться все типы закреплений и все виды силовых нагрузок. Температурные воздействия задаются также как и в статическом анализе. Задание закреплений и силовых нагрузок является обязательным условием выполнения корректного расчёта. Суммарно наложенные на модель ограничения должны удовлетворять следующему условию:

Для обеспечения анализа устойчивости модель должна иметь закрепление, исключающее её свободное перемещение в пространстве как твёрдого тела. Невыполнение этого условия приведёт к неверным результатам конечно-элементного моделирования или срыву вычислительного процесса.

Отметим также, что задание нагрузок имеет большое значение для обеспечения корректности постановки задачи расчёта начальной устойчивости. В частности, при определенных случаях нагружения, решение задачи может не иметь физического смысла (например, стержень, растягиваемый продольной силой). Признаком корректно заданных граничных условий является положительное значение коэффициента критической нагрузки, полученного в результате расчёта.

3.Выполнение расчёта. Перед выполнением расчёта пользователь указывает в свойствах задачи алгоритмы расчёта и количество форм потери устойчивости, которые он хочет анализировать.

В информационное окно при выполнении расчёта выводится следующая справочная информация:

Количество узлов – количество узлов расчётной конечно-элементной сетки.

Количество элементов – количество тетраэдров в конечно-элементной сетке.

Введено аргументов – количество уравнений, участвующих в решении.

Расчёт закончен – символизирует о том, что процесс решения завершился успешно.

4.Результаты. Результатами анализа устойчивости являются:

Коэффициент критической нагрузки – расчётное значение коэффициента, произведение которого на приложенные к системе нагрузки, даёт фактическое значение критической нагрузки, приводящей систему в новое равновесное состояние. Например, для модели приложена распределенная сила 1000 Н. Коэффициент критической нагрузки по результатам расчёта составил 109,18. Это означает, что первая форма устойчивого равновесного состояния для данной модели имеет критическую нагрузку 109180 Н.

123

Руководство пользователя T-FLEX Анализ

Коэффициент критической нагрузки должен быть положительным. Если в результате решения коэффициент критической нагрузки получился отрицательным, это означает, что при приложенных к конструкции нагрузках состояние потери устойчивого равновесия не может быть достигнуто.

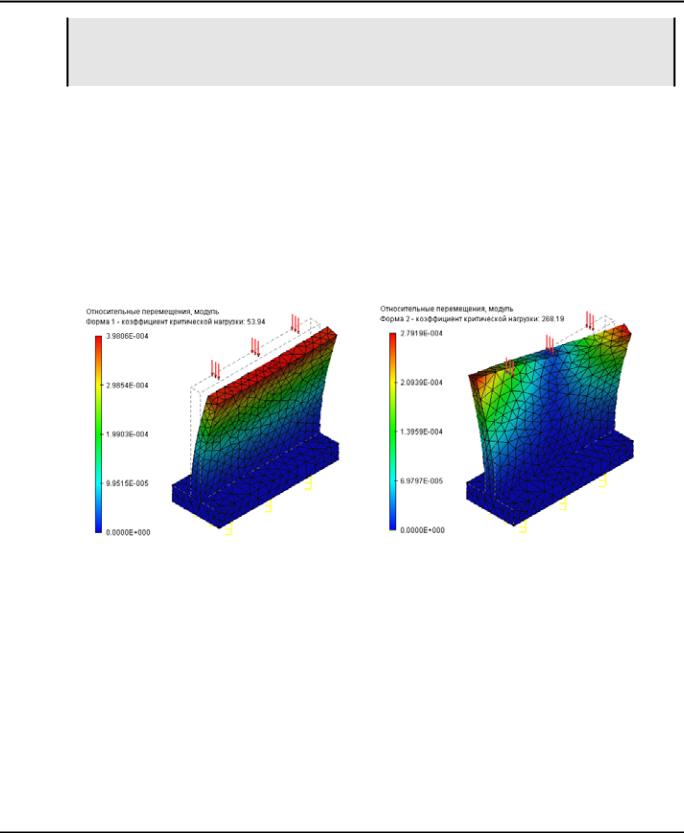
Относительные перемещения, соответствующие данной критической нагрузке. Этот тип результата отражает форму равновесного устойчивого состояния конструкции, соответствующую определенной критической нагрузке. Формы равновесных состояний, отображаемые в окне постпроцессора после завершения расчёта, представляют собой относительные перемещения. Анализируя эти формы, можно сделать заключения о характере перемещений в ситуации потери устойчивости. Зная ожидаемую равновесную форму на некоторой критической нагрузке, можно, например, задать дополнительное закрепление или опору в области конструкции, соответствующей максимуму данной формы равновесного состояния, что приведёт к эффективному изменению механических свойств изделия.

В качестве дополнительного (справочного) результата можно вывести также перемещения конструкции под действием приложенных статических нагрузок, расчёт которых предшествует расчёту коэффициентов критических нагрузок.

Формы равновесных состояний, соответствующие первой и второй критическим нагрузкам детали

Алгоритм оценки устойчивости по результатам моделирования

После успешного расчёта задачи необходимо проанализировать результаты расчётов, чтобы сделать заключение о вероятной устойчивости конструкции по результатам конечно-элементного моделирования. Примерная последовательность действий по оценке результатов конечноэлементного моделирования явления начальной устойчивости следующая:

1.Оценка корректности решения. Как уже отмечалось, коэффициент критической нагрузки должен быть положительным. Если коэффициент получился отрицательным, значит нагружения, приложенные к конструкции, не вызывают эффектов неустойчивого поведения системы.

2.Оценка значения коэффициента. Если коэффициент критической нагрузки получился положительным и меньше 1, это означает, что при заданных нагружениях система потеряет устойчивость, и конструкция нуждается в доработке. Если коэффициент критической нагрузки положителен и больше 1, значит, при заданных условиях нагружения потеря устойчивости конструкции не угрожает.

124