
- •Содержание
- •Введение
- •Технические требования
- •Требования к компьютеру
- •Рекомендуемые параметры вычислительной техники для эффективной (профессиональной) работы с T-FLEX Анализом
- •Установка системы T-FLEX Анализ
- •Структурная организация приложения T-FLEX Анализ
- •Этапы анализа конструкций
- •Быстрое начало
- •Шаг 1. Подготовка объёмной твердотельной модели изделия
- •Шаг 2. Создание «Задачи»
- •Шаг 3. Назначение материала
- •Шаг 4.1 Наложение граничных условий. Задание закреплений
- •Шаг 4.2 Наложение граничных условий. Задание нагружений
- •Шаг 5. Выполнение расчёта
- •Шаг 6. Анализ результатов расчёта
- •Подготовка конечно-элементной модели для Анализа (Препроцессор)
- •Виды конечно-элементных моделей
- •Назначение и роль сеток
- •Виды и роль граничных условий
- •Управление «Задачами», команды управления задачами
- •Общие свойства задач
- •Задание материала
- •Построение сетки
- •Параметры сетки
- •Задание ограничений
- •Полное закрепление
- •Частичное закрепление
- •Контакт
- •Упругое основание
- •Задание нагрузок
- •Механические нагрузки
- •Сила
- •Давление
- •Вращение
- •Ускорение
- •Цилиндрическая нагрузка
- •Крутящий момент
- •Осциллятор
- •Дополнительная масса
- •Тепловые нагрузки
- •Температура
- •Тепловой поток
- •Тепловая мощность
- •Конвективный теплообмен
- •Излучение
- •Сводная таблица нагрузок
- •Редактирование нагрузок и закреплений
- •Настройки и сервисные команды
- •Работа с 3D окном при подготовке элементов задач
- •Особенности работы с параметрической моделью
- •Экспорт
- •Обработка результатов (Постпроцессор)
- •Общие принципы работы с результатами
- •Настройки и сервисные команды окна результатов расчёта
- •Настройка окна результатов расчёта
- •Настройка цветовой шкалы
- •Использование датчиков для анализа результатов
- •Использование графиков для анализа результатов
- •Интегральное значение
- •Построение сечений
- •Генерация отчётов
- •Пример интерпретации результата
- •Статический анализ
- •Особенности этапов статического анализа
- •Алгоритм оценки статической прочности по результатам моделирования
- •Настройки процессора линейной и нелинейной статики
- •Задача оптимизации
- •Задача об оптимизации толщины балки
- •Приложение (справочные материалы)
- •Характеристики конструкционных материалов
- •Объёмное напряжённо-деформированное состояние в точке
- •Оценка статической прочности конструкций. Теории прочности
- •Анализ устойчивости
- •Особенности этапов анализа на устойчивость
- •Алгоритм оценки устойчивости по результатам моделирования
- •Настройки Процессора анализа устойчивости
- •Частотный анализ
- •Особенности этапов частотного анализа
- •Настройки Процессора частотного анализа
- •Вынужденные колебания
- •Вводные сведения
- •Особенности этапов анализа вынужденных колебаний
- •Настройки препроцессора анализа вынужденных колебаний
- •Настройки процессора анализа вынужденных колебаний
- •Настройки постпроцессора и анализ результатов вынужденных колебаний
- •Анализ Усталости
- •Цикл напряжений. Основные характеристики
- •Кривая усталости
- •Методы коррекции напряжений
- •Оценка характеристик сопротивления усталости при сложном напряженном состоянии
- •Этапы анализа усталости
- •Результаты усталостного расчёта
- •Примеры расчётов деталей на усталостную прочность
- •Однособытийный усталостный расчет
- •Многособытийный усталостный расчет
- •Примеры результатов однособытийного усталостного расчёта
- •Пример результатов многособытийного усталостного расчёта
- •Тепловой анализ
- •Особенности этапов теплового анализа
- •Настройки Процессора теплового анализа
- •Примеры тепловых расчётов
- •Тепловой расчёт радиатора охлаждения. Установившийся режим
- •Расчёт времени нагревания радиатора охлаждения. Нестационарный режим
- •Расчёт времени остывания радиатора охлаждения. Нестационарный режим
- •Верификационные примеры
- •Примеры расчётов задач статики
- •Изгиб консольно-защемлённой балки под действием сосредоточенной нагрузки
- •Статический расчет круглой пластины, защемленной по контуру
- •Расчет сферического сосуда давления
- •Квадратная пластина под силой в центре
- •Цилиндрический резервуар со стенками постоянной толщины
- •Кручение бруса с круглым поперечным сечением
- •Стержень под действием собственного веса
- •Расчёт вращающегося сплошного диска постоянной толщины
- •Свободно опертая прямоугольная пластинка под синусоидальной нагрузкой
- •Температурные напряжения биметаллического элемента
- •Примеры расчётов задач устойчивости
- •Расчет устойчивости сжатого прямого стержня
- •Устойчивость квадратной пластины
- •Устойчивость прямоугольной пластины
- •Примеры задач частотного анализа
- •Определение собственных частот колебаний балки
- •Определение первой собственной частоты колебаний круглой пластинки
- •Свободные колебания сферического купола
- •Примеры задач теплового анализа
- •Установившаяся температура
- •Поток тепла в шаре
- •Теплопроводность цилиндрической стенки
- •Литература

Статический анализ
парности касательных напряжений: касательные напряжения, действующие по двум взаимно перпендикулярным площадкам в направлениях, ортогональных ребру, образованному пересечением этих площадок, равны по величине. С учетом этих свойств из девяти компонент тензора напряжений независимыми оказываются шесть компонент.
Также как и для деформаций для напряжений вводят понятие главных напряжений, σ1 ≥σ2 ≥σ3 ,
соответствующих главным деформациям, которые связаны с компонентами тензора напряжений уравнением:
σ3 − J1σ 2 + J2σ − J3 = 0 , где
|
|
|
|
σx τxy |
|
σx |
τxz |
|
|
σ y |
τyz |
|
|
σ |
x |
|
J1 =σx +σ y +σz , |
J2 |
= |
|
+ |
+ |
|
, |
|
|
|||||||
|
τ yx |
σ y |
τzx |
σz |
|
τzy |
σz |
J3 = τ yx |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τzx |
||
τxy |
τxz |
||
σ y |
|
|
|
τyz |
|||
τ |
zy |
σ |
|
|
|
z |
|
Решение кубического уравнения имеет три вещественных корня σ1,σ2,σ3 , которые обычно упорядочиваются в виде σ1 ≥σ2 ≥σ3 . Главные напряжения обладают важным свойством: по
сравнению со всеми другими площадками нормальные напряжения на главных площадках принимают экстремальные значения. Вводится также понятие среднего напряжения по формуле:
σ0 = (σx +σy +σz ) / 3 = (σ1 +σ2 +σ3 ) / 3
Оценка статической прочности конструкций. Теории прочности
Под предельным опасным напряжённым состоянием понимается такое, при котором происходит качественное изменение свойств материала − переход от одного механического состояния к другому. Для пластичных материалов предельным обычно считается напряженное состояние, соответствующее возникновению заметных остаточных деформаций, а для хрупкого − такое, при котором начинается разрушение материала. Предельное состояние материала допустить нельзя. Поэтому при расчёте на прочность ориентируются на так называемое допускаемое состояние. Оно соответствует нагрузке, полученной путём деления нагрузки, вызывающей предельное состояние, на некоторый коэффициент запаса. Если в двух напряжённых состояниях коэффициенты запаса равны, то они называются равноопасными. Для сравнения различных напряжённых состояний за эталон
(эквивалент) принято простое растяжение (сжатие) с главным напряжением σэкв .
Эквивалентное напряжение σэкв - это напряжение, которое следует создать в растянутом образце, чтобы его напряжённое состояние было равноопасно заданному напряжённому состоянию. Условие прочности записывается в виде σэкв ≤ [σ].
Теории прочности представляют собой гипотезы о критериях, определяющих условия перехода материала в предельное состояние.
119

Руководство пользователя T-FLEX Анализ
Первая теория прочности
В первой теории прочности за критерий перехода материала в предельное состояние принимается наибольшее нормальное напряжение. Согласно этой теории, опасное состояние наступает тогда, когда какое-либо из главных напряжений достигает опасного значения. В соответствии с этим при расчетах на прочность ограничивается величина наибольших главных напряжений, которая не
должна превышать допускаемого нормального напряжения [σ]. Условие прочности имеет вид:
σэквI ≤ [σ],
где σэквI = σ1 , если σ1 ≥ σ3 и σэквI = σ3 , если σ1 ≤ σ3 .
Вторая теория прочности
Во второй теории прочности за критерий принимается наибольшая деформация. Согласно этой теории опасное состояние материала наступает тогда, когда линейные деформации достигают
некоторого |
опасного |
значения. |
Для пластичного материала условие прочности имеет |
вид |
|||||||||||||
max |
|
ε |
|
≤[ε], |
|
[ε]= [σE |
]. |
|
|
max |
|
ε |
|
=ε1 = |
1 |
[σ1 −ν(σ2 +σ3 )], |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
где |
Если, |
например |
|
|
E |
то |
|||||||||
|
|
|
|
||||||||||||||
|
|
||||||||||||||||
σ эквII = σ 1 −ν (σ 2 + σ 3 )≤ [σ ]. |
|
|
|
|
|
|
|
|
|
|
|
||||||
Для хрупкого материала условие прочности имеет вид:
|
[σ |
р |
] |
|
|
|
|
σ |
с ] |
||
εmax ≤ [εр ]= |
|
|
|
|
|
εmin |
≤ [εс ]= |
[ |
|
||
|
|
|
|
|
|
|
|
||||
|
E |
|
|
, |
|
|
|
|
E |
||
Первая теория дает удовлетворительное совпадение с опытными данными только для хрупких материалов. Вторая практически в настоящее время не применяется.
Третья теория прочности
В третьей теории прочности критерием принимается наибольшее касательное напряжение. Согласно этой теории опасное состояние наступает, если наибольшие касательные напряжения достигают опасного значения.
Условие прочности имеет вид: τmax = |
σ1 −σ3 |
, где |
[τ] |
= |
[σ |
] |
. Откуда: |
||
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
σ эквIII |
=σ1 −σ3 |
≤[σ] |
|
||||
Четвертая (энергетическая) теория прочности
Четвертая теория прочности - энергетическая, представляет собой гипотезу о том, что причиной возникновения опасного состояния является величина удельной потенциальной энергии изменения формы uф, то есть критерий – удельная потенциальная энергия изменения формы.
Формулу удельной потенциальной энергии изменения формы получим из формулы полной удельной потенциальной энергии деформации, подставляя значение коэффициента Пуассона равного µ=0,5.
Получим:
[uô ]= 13Å+ μ (σ12 +σ22 +σ32 −σ1σ2 −σ2σ3 −σ1σ3)
120
Статический анализ
Условие прочности имеет вид uф u |
≤ [u |
], где |
[u |
ô |
]= |
1+ μ |
|
[σ]. |
|
|
||||||
|
|
ф |
ф |
|
|
|
|
3Å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
σ IV |
= σ 2 |
+σ 2 |
+σ 2 |
−σ σ |
2 |
−σ |
2 |
σ |
3 |
−σ σ |
3 |
≤ [σ] |
|||
|
экв |
1 |
2 |
3 |
|
1 |
|
|
|
|
1 |
|
||||
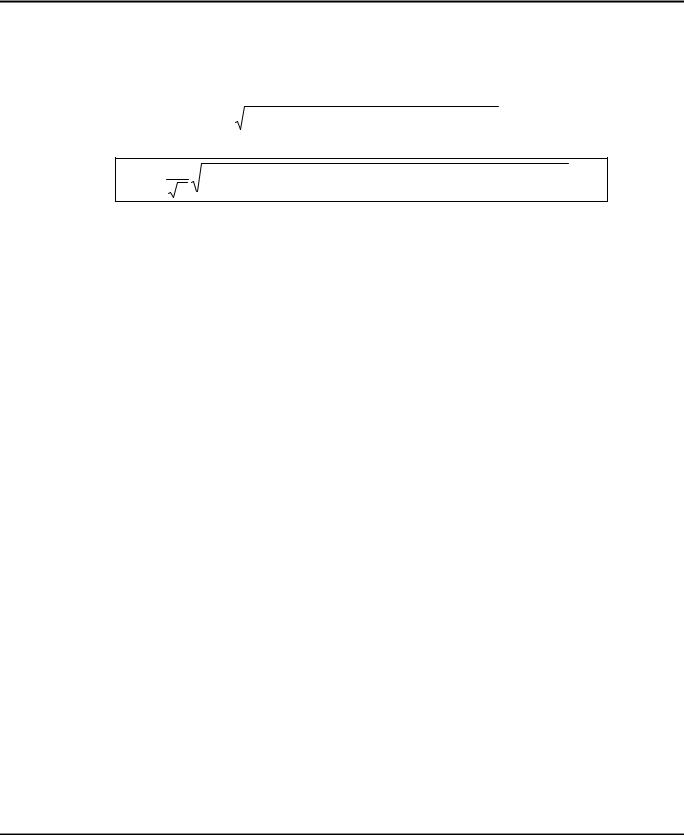
или
σэквIV |
= |
1 |
(σx −σ y )2 + (σ y −σz )2 +(σz −σx )2 +6(τxy2 |
+τ2yz +τxz2 ) ≤ [σ] |
|
|
2 |
|
|
Третья и четвертая теории прочности дают удовлетворительное совпадение результатов теоретического расчета с опытными данными для пластичных материалов и широко применяются при расчетах на прочность. Для хрупких материалов эти теории не применимы.
121
