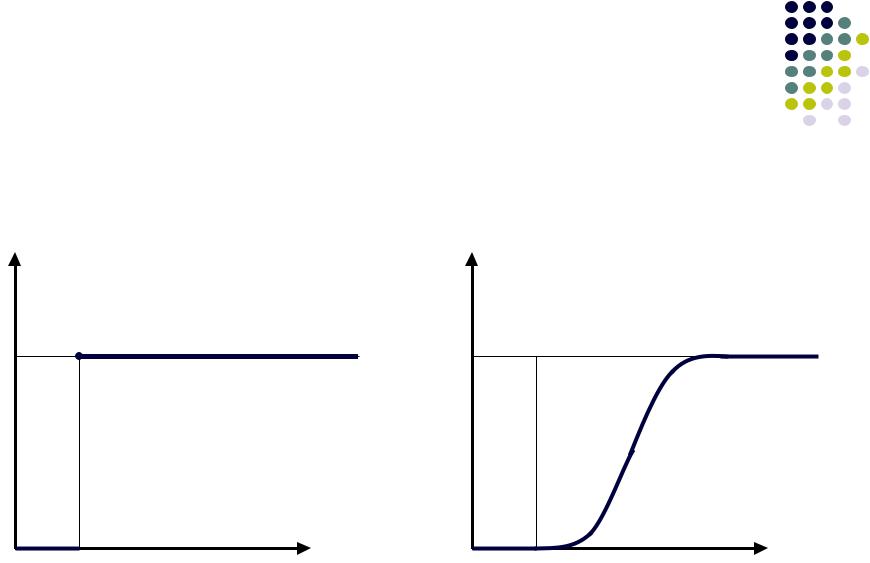
Примеры непрерывных нечетких множеств (2)
Четкое множество |
|
Нечеткое множество |
x > b |
|
x >> b |
µ |
µ |
(x намного больше b ) |
1 |
1 |
|
b
x
b
x
Специальные главы интеллектуальных систем. Установочная лекция |
17 |
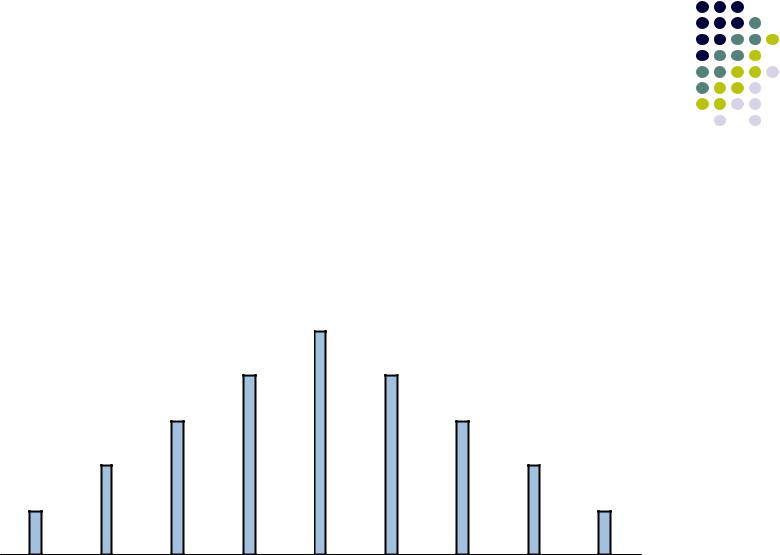
Пример дискретного нечеткого |
||||||
множества |
|
|
|
|
|
|
Множество целых чисел, близких к 1 |
|
|
|
|||
A = {0,2/–3; 0,4/–2; 0,6/–1; 0,8/0; 1/1; 0,8/2; 0,6/3; 0,4/4; 0,2/5} |
||||||
|
|
1 |
|
|
|
|
|
0,8 |
|
0,8 |
|
|
|
0,6 |
|
|
|
0,6 |
|
|
0,4 |
|
|
|
|
0,4 |
|
0,2 |
|
|
|
|
|
0,2 |
-3 -2 -1 |
0 |
1 |
2 |
3 |
4 |
5 |
Специальные главы интеллектуальных систем. Установочная лекция |
|
|
18 |
|||
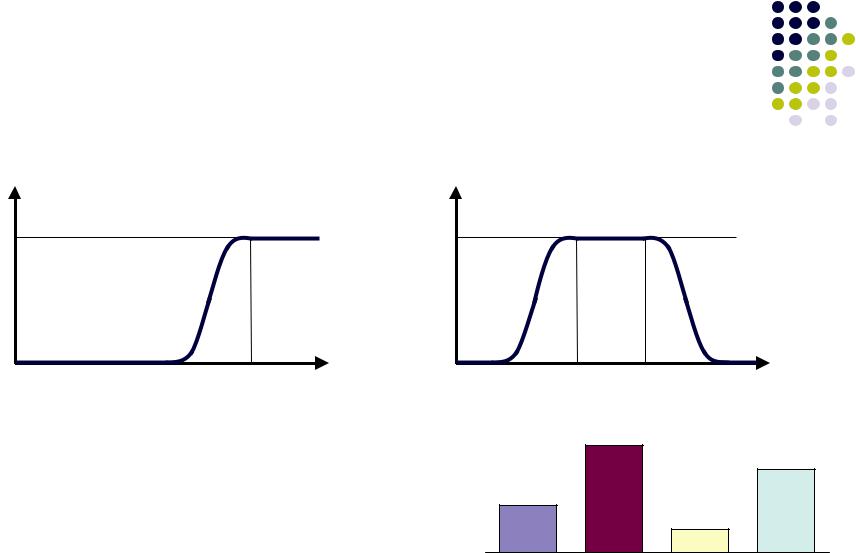
Примеры формализации нечетких понятий
µ Высокий рост |
µ |
1 |
1 |
170 185 |
см |
Интересная книга
X = {Книга_1, Книга_2, Книга_3, Книга_4}
A = {0,4/Книга_1; 0,9/Книга_2; 0,2/Книга_3; 0,7/Книга_4}
Средняя скорость
60 80 |
км/ч |
|
0,9 |
|
0,7 |
0,4 |
|
|
|
|
0,2 |
|
|
|
|
|
|
Книга_1 |
Книга_2 |
Книга_3 |
Книга_4 |
Специальные главы интеллектуальных систем. Установочная лекция |
19 |
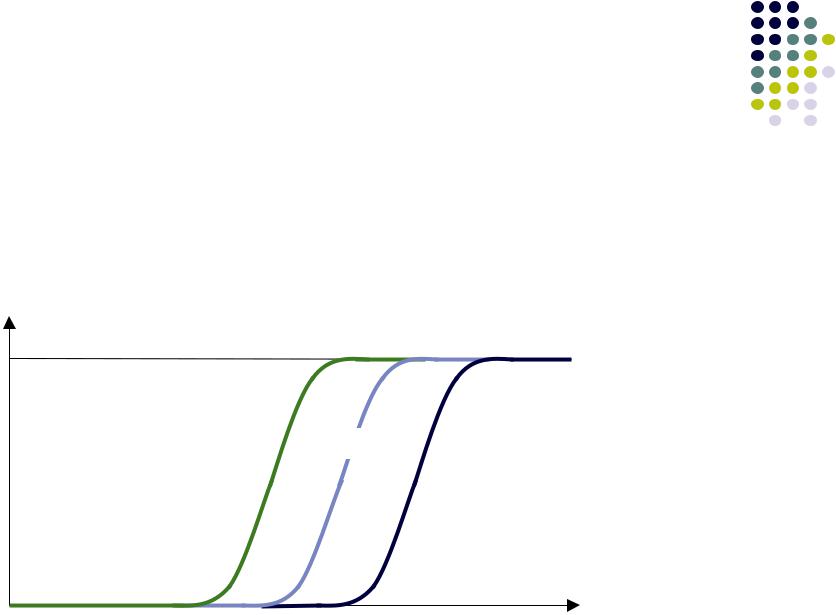
Субъективность функции принадлежности
Вид функции принадлежности зависит от того, что вкладывается в соответствующее понятие конкретным
экспертом и/или определяется условиями конкретной задачи
µ
Высокий рост
1
в Китае
в Европе
в NBA
см
Специальные главы интеллектуальных систем. Установочная лекция |
20 |