
Метод. указания к РГР
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Брянский государственный технический университет»
МЕХАНИКА МАТЕРИАЛОВ
И
ОСНОВЫ КОНСТРУИРОВАНИЯ
Брянск 2013
ПРЕДИСЛОВИЕ
Программой курса «Механика материалов и основы конструирования» (ММ и ОК) предусмотрено изучение важнейших разделов дисциплин «Сопротивление материалов» и «Детали машин и основы конструирования», являющихся фундаментом общепрофессиональной подготовки студентов.
Порядок выполнения заданий по курсу ММ и ОК построен на принципе органического единства традиционных дисциплин подготовки бакалавров к проектно-конструкторской профессиональной деятельности. Их выполнение способствует обобщению, углублению и закреплению знаний, полученных при изучении курса, для последующего применения их при комплексном решении задачи проектирования механизмов электромеханического привода.
Методические указания содержат задания по шести основным разделам курса. В каждом разделе приведён пример решения типовой задачи. Указан список литературных источников по разделам курса и сборников задач с примерами их решения.
Номер схемы для выполнения задания соответствует последней цифре номера зачетной книжки, а номер варианта числовых значений параметров – предпоследней цифре. Например, если номер зачётной книжки 901638, то нужно выполнять задание, соответствующее расчетной схеме 8 и числовым значениям параметров по варианту 3. Цифра ноль соответствует десятому варианту или десятой схеме задания.
Расчётно-графические работы оформляются в виде пояснительной записки, содержащей формулы, расчётные схемы, эпюры, числовые значения параметров, результаты вычислений и краткие пояснения выполняемых действий.
2
1. РАСТЯЖЕНИЕ (СЖАТИЕ) СТЕРЖНЕЙ
Задание 1. К стальному (Ест, т) или чугунному (Еч, вр, вс) стержню (брусу) переменного сечения площадью Аi приложены сосредоточенные силы F1 и F2 и распределенная нагрузка интенсивностью q согласно схеме (рис. 1). Определить коэффициент запаса прочности стержня (по его величине сделать вывод о разрушении) и перемещение его не опёртого конца. Исходные данные для расчета приведены в табл. 1.
Таблица 1
Исходные данные к заданию 1
|
|
Числовые значения параметров по вариантам |
|
|||||||
Параметр |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
F1, кН |
60 |
80 |
50 |
80 |
40 |
20 |
40 |
80 |
60 |
70 |
F2, кН |
40 |
20 |
60 |
50 |
60 |
80 |
80 |
20 |
20 |
50 |
|
|
|
|
|
|
|
|
|
|
|
q, кН/м |
200 |
400 |
100 |
200 |
100 |
100 |
200 |
400 |
100 |
200 |
|
|
|
|
|
|
|
|
|
|
|
L, м |
0,2 |
0,1 |
0,4 |
0,3 |
0,2 |
0,4 |
0,3 |
0,1 |
0,4 |
0,25 |
А104 м2 |
4 |
6 |
2 |
8 |
4 |
5 |
4 |
8 |
6 |
2 |
Материал |
Сталь |
Чугун |
Чугун |
Сталь |
Чугун |
Чугун |
Сталь |
Сталь |
Чугун |
Чугун |
T, МПа |
300 |
- |
- |
340 |
- |
- |
380 |
650 |
- |
- |
вр, МПа |
- |
120 |
280 |
- |
150 |
180 |
- |
- |
150 |
200 |
вс, МПа |
- |
500 |
1000 |
- |
600 |
700 |
- |
- |
600 |
780 |
3
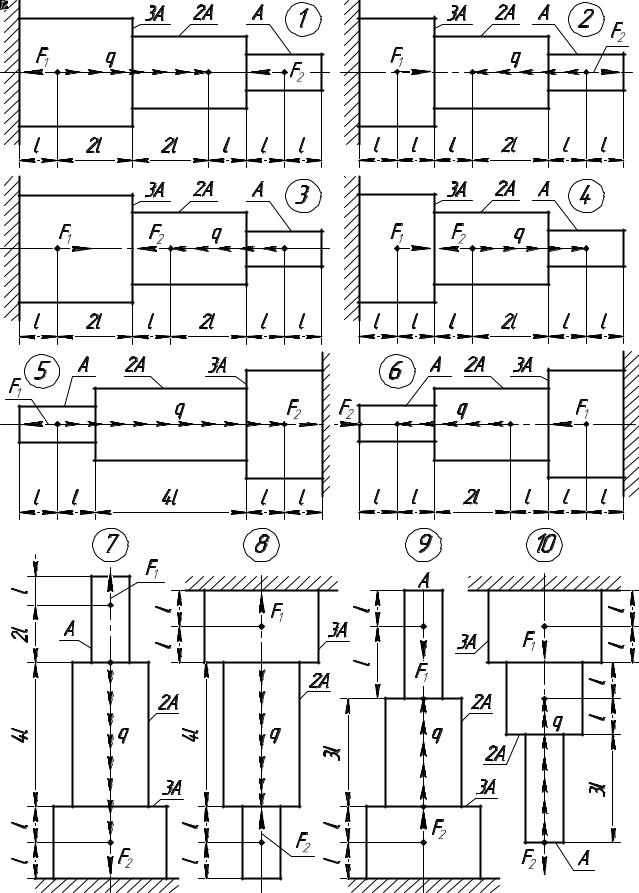
Рис. 1. Расчётные схемы к заданию 1. В кружках – номера вариантов
4
Указания по выполнению задания
1.Построить эпюру продольных сил N , применяя метод сечений.
2.Построить эпюру нормальных напряжений по эпюре N, используя зависимость N / А.
3.Найти максимальное значение напряжений mах на эпюре . Определить коэффициент запаса прочности по формуле S lim / max ,
где |
lim |
– предельные напряжения для пластических материалов |
lim |
тр |
тс , для хрупких - и lim= вр или lim= вс , max – макси- |
мальные напряжения в стержне. Предел текучести т и пределы
прочности при растяжении σвр и сжатии σвс |
определяют по таблицам |
|||||
[6 – 8] в зависимости от марки материала. Если m ax lim |
( S 1), |
|||||
то наступает разрушение конструкции. |
|
|
||||
|
4. Построить эпюру перемещений сечений стержня по зависимо- |
|||||
сти |
li Nili |
/ (Ei Ai ) . Определить перемещение неопёртого (свобод- |
||||
ного) |
конца |
стержня. Принять |
модули |
упругости для |
стали |
|
Е |
|
2 105 МПа, для чугуна – Е |
105 МПа. |
|
||
ст |
|
|
ч |
|
|
|
ПРИМЕР РАСЧЕТА
К чугунному брусу (стержню) переменного сечения площадью Аi приложены сосредоточенные силы F1 40 кН, F2 60 кН и распределённая нагрузка q 200 кH/м согласно схеме (рис. 2). Определить коэффициент запаса прочности бруса и перемещение его свободного конца, если площадь сечения A 4 10 4 м2, а длина l 0,2 м.
Решение
1. Разбиваем стержень на силовые участки, в пределах которых силовой фактор описывается одним математическим выражением. Границами участков являются границы стержня и сечения (точки), в которых приложены нагрузки. Стержень содержит четыре силовых участка. Определение опорной реакции в защемлении (заделке) не является обязательным, так как внутренние продольные усилия в сечениях стержня можно найти методом сечений, перемещаясь вдоль продольной оси (оси z) от свободного конца стержня к защемлению (на рис. 2, а – сверху вниз).
5
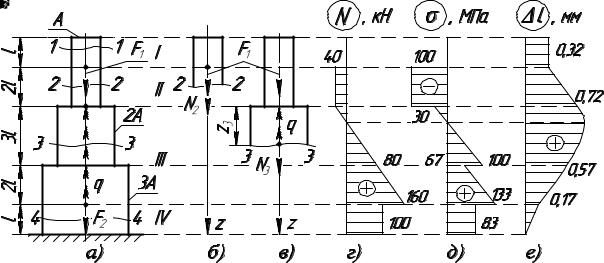
Рис. 2. К расчету стержня на растяжение (сжатие): а – расчетная схема стержня; б – расчетная схема для второго участка; в – расчетная схема для третьего участка; г – эпюра продольной силы; д – эпюра напряжений; е – эпюра удлинений стержня
Мысленно проведём на первом силовом участке сечение 1-1 и, отбросив нижнюю часть стержня, рассмотрим равновесие верхней части. На первом участке внешние силовые факторы отсутствуют, поэтому внутреннее продольное усилие N1 0.
Выполним аналогичные операции на втором силовом участке. К верхней части стержня сечения 2-2 приложим внутреннее растягивающее продольное усилие, которое условно считаем положительным (направлено от сечения 2-2 вдоль оси z), и внешнюю силу F1 (рис. 2, б). Под действием этих сил верхняя часть стержня находится в равновесии.
Для второго участка уравнение статического равновесия
Zi 0; |
N2 F1 0; |
N2 F1 40 кН. Знак минус показывает, что внутренняя продольная сила – сжимающая и постоянная на всем участке. Эпюра продольной силы N2 на втором участке ограничивается прямой, параллельной базисной линии (рис. 2, г).
Аналогично мысленно выполним сечение 3-3 на третьем участке (рис. 2, в). Переменная координата изменяется от 0 до 5l, (5l z3 0). Условия равновесия верхней части стержня на третьем участке имеют вид
Zi 0; N3 F1 qz3 0 ; N3 F1 qz3 ; 5l z3 0
6
вначале третьего участка при z3 0 N3 0 F1 q 0 F1 40 кН (сжатие);
вконце третьего участка при z3 5l
N3 (5l) F1 q 5l 40 200 5 0,2 160 кН (растяжение).
Эпюра продольной силы N3 на третьем участке представляется наклонной прямой (рис. 2, г), так как q const , а переменная z3 в первой степени.
При определении внутреннего продольного усилия методом сечений нет необходимости всякий раз изображать отсеченную часть бруса. Достаточно мысленно выполнить изображенные на рис. 2, а и 2, б действия, направить внутреннее продольное усилие от сечения (как растягивающее усилие) и написать уравнение статического равновесия отсеченной части стержня. Для четвёртого участка (сечение 4-4) оно имеет вид
N4 F1 q 5l F2 0; N4 F1 q 5l F2 40 200 5 0,2 60 100
кН (растяжение).
Продольная сила N4 - растягивающая и постоянная на всем четвертом участке, изображенная на эпюре прямой, параллельной базисной линии (рис. 2, г). При определенном навыке можно пропускать уравнение статического равновесия, а записывать выражение для N сразу, учитывая внешние силовые факторы со знаком плюс, если они направлены от рассматриваемого сечения, и минус, если они направлены в сторону рассматриваемого сечения.
2. Построим эпюру нормальных напряжений σ для определения максимальных напряжений. Напряжение на первом участке постоянное и равное
1 N1 / A 0 .
На втором участке нормальное напряжение постоянно и равно:
2 N2 / A 40 10 4 / 4 10 4 100 106 Н/м2 100 МПа.
На третьем участке напряжения переменные, так как продольная сила изменяется линейно N3 (z3 ) и изменяется площадь сечения. В
начале третьего участка
3 (0) N3 (0) / (2A) ( 40 103 ) / (2 4 10 4 ) 50 106 Н/м2 50 МПа.
На расстоянии z3 2l при площади сечения 2А:
N3 (3l) F1 q 3l 40 200 3 0,2 80 кН (растяжение).
7
3 (3l) N3 (3l) / (2A) (80 103 ) / (2 4 10 4 ) 100 106 Н/м2 100 МПа.
Там же при площади 3А
3 (3l) N3 (3l) / (3A) (80 103 ) / (3 4 10 4 ) 67 106 Н/м2 67 МПа.
Вконце третьего участка:
3 (5l) N3 (5l) / (3A) (160 103 ) / (3 4 10 4 ) 133 106 Н/м2 133 МПа.
|
На четвертом участке: |
|
|
4 N4 / (3A) (100 103 ) / (3 4 10 4 ) 83 106 |
Н/м2 83 МПа. |
|
По полученным значениям напряжений строим эпюру σ (рис. 2, |
|
д). |
Видно, что максимальное нормальное напряжение в стержне |
|
max |
133 МПа. |
|
|
Коэффициент запаса прочности |
|
Slim / max вр / max 150 /133 1,13.
3.Определим перемещения на каждом силовом участке стержня. На первом силовом участке перемещения
l1 N1 l1 / (Er A2 ) 0 , так как N1=0. На втором участке перемещения
l2 N2 l2 / (Er A2 ) N2 2l / (Er A) ( 40 103 2 0,2) / (105 106 4 104 ) 4 10 4
0,4 мм (сокращение длины). Перемещение на третьем участке
l3 l3 l3 ,
где ∆l3' – перемещение подучастка третьего участка с меньшим сечением площадью 2А, а ∆l3'' – перемещение подучастка с бóльшим сечением 3A;
l3' N3(0) l3' / Er A3' q(l3)2 / 2Er A3' N3(0) 3l / Er 2A q(3l)2 / 2Er 2A ;l3' 40 103 3 0,2 / 105 106 2 4 10 4 200 103 (3 0,2)2 / 2 105 106 2 4 10 4 ;
l3' 3 10 4 4,5 10 4 0,15 мм (удлинение);
l3'' N3(3l) l3'' / Er A3'' q(l3'' )2 / 2Er A3'' N3(3l) 2l / Eч 3A q(2l)2 / 2Eч 2A ;
l3'' 80 103 2 0,2 / 105 106 3 4 10 4 200 103 2 0,2 2 / 2 105 106 3 4 10 4 ;
l3'' 2,7 104 1,3 10 4 4 10 4 м 0,4 мм (удлинение);l3 0,15 0,4 0,55 мм
Перемещение на четвертом участке
l4 N4 l4 / (Er A4) N4 l / (Er 3A) (100 103 0,2)/ (105 106 3 4 10 4) 1,7 10 4 м =
8
0,17 мм (удлинение).
Построение эпюры перемещений сечений стержня ∆l начинают от защемления, где перемещение защемлённого сечения l 0. Тогда на границе четвертого и третьего участков оно составит l 0,17 мм. На третьем участке перемещения сечений изменяются по параболе. В месте изменения размеров перемещение сечения составит
l l4 l3'' 0,17 0,4 0,57 мм.
Перемещение на границе третьего и второго участков:
l l4 l3'' l3' 0,17 0,4 0,15 0,72 мм.
Первый силовой участок не нагружен внешними силами, поэтому не даёт приращения перемещения ( l1 0). Перемещение свободного
конца стержня (рис. 6, е)
l l4 l3'' l3' l2 l1 0,17 0,4 0,15 0,4 0 0,32 мм.
Эпюра на первом участке изображена прямой, параллельной базисной линии. Перемещение (удлинение) свободного конца l 0,32 мм.
2. КРУЧЕНИЕ СТЕРЖНЕЙ
Задание 2. Круглый стальной брус диаметром d1, одним концом жёстко закрепленный в заделке, воспринимает действие сосредоточенных, вращающих (скручивающих) моментов Ti (рис. 3). Построить эпюры крутящих моментов, касательных напряжений и углов закручивания. Определить коэффициент запаса прочности бруса, если модуль сдвига стали G 8 104 МПа, предельные касательные напряжения lim 170 МПа. Исходные данные для расчета даны в табл. 2.
Указания по выполнению задания
1.Построить эпюру крутящих моментов T, применяя метод сече-
ний.
2.Построить эпюру касательных напряжений τ, используя эпюру
Ти зависимость Т / Wp .
3.Найти максимальное значение напряжений τmах на эпюре τ и определить коэффициент запаса прочности по формуле S lim / max , где τlim –
предельные напряжения, для пластических материалов lim T , для хрупких - lim в. Пределы текучести τт и прочности τв определяют по таб-
9
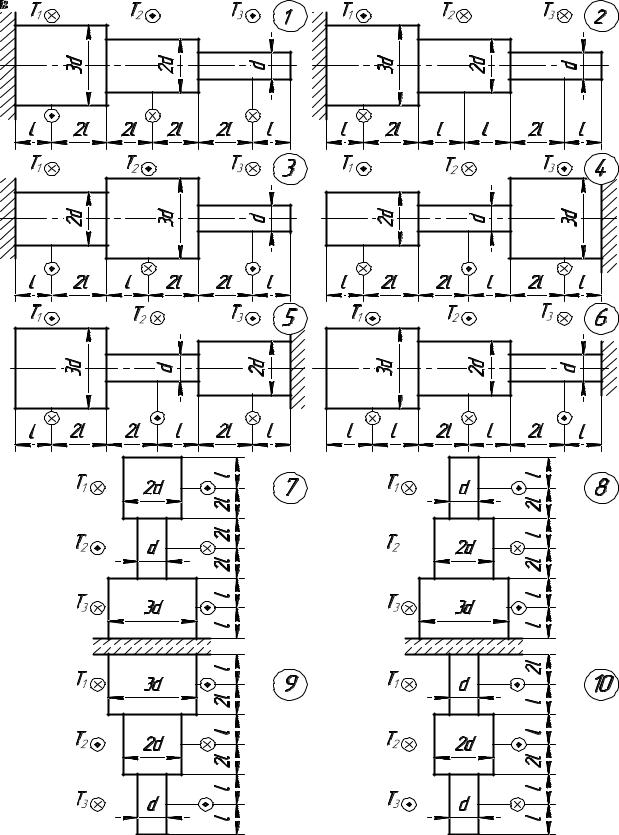
лицам в зависимости от марки материала. Если max lim (S 1), то наступает разрушение конструкции.
Рис. 3. Расчетные схемы к заданию 2. В кружках – номера вариантов
10
