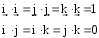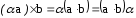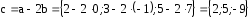Билет№13 Векторное произведение векторов

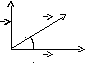Правая тройка(угол поворота от 1-го ко 2-му векторам

b

c

будет против часовой стрелки)

а

b

с

Левая тройка (угол поворота от 1-го ко 2-му векто-

а

рам будет по часовой стрелки)

Опр: векторным произведением векторов 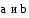называетсявектор, который:

1. Перпендикулярен каждому из известных векторов

2. Образует данную векторами правую тройку

3. Имеет длину равную площади параллелограмма построенного на заданных векторах

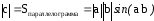
Свойства векторного произведения векторов

1. При смене мест множителей векторное произведение меняет знак

2. 

3. 

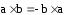
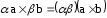
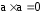
4. (произведение коллинеарных векторов равно 0)

Замечание: для векторного произведения векторов не существует понятие квадрата

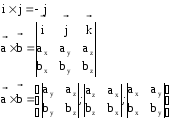
ПРИМЕНЕНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ

1. Два вектора параллельны тогда и только тогда, когда их векторное произведение равно нулю

2. Площадь параллелограмма построенного на векторах равна длине векторного произведения этих векторов

3. Площадь треугольника построенного на векторах равна половине длины векторного произведения этих векторов

4. 

5. 

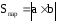
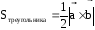
Дано:

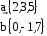
Найти:

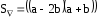
Решение

1. 

2. 

3. 

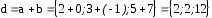
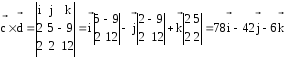
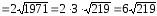
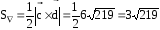4. - ответ

Билет№14 Смешанное произведение векторов

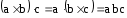
Результат – число

Смешанное произведение задает объем параллелепипеда, построенного на векторах a,b,c с точностью до знака.

Если тройка векторов a,b,c является правой, то смешанное произведение совпадает с величиной объема парал-да.

Если тройка векторов явл-ся левой, то смешанное произведение векторов численно равно числу противоположному значению объема

Св-ва смешанного произведения:

1. Смешанное произведение не меняется при смене знака векторного и скалярного произведения

1

2

Замечание: если в выражении отсутствуют скобки, то есть различные знаки векторного и скалярного произведения. Приоритет отдается векторному произведению

1

2

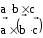
2. Смешанное произведение не меняется при циклической перестановке векторов.

3. При перестановке 2-х соседних векторов смешанное произведение меняет знак.

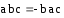
4. Смешанное произведение = «-», когда векторы компланарны.