6. Собственные значения и собственные векторы линейного оператора

Постановка задачи

Найти собственные значения и собственные векторы линейного оператора Α, заданного в некотором базисе матрицей А.

План решения

Составляем характеристическое уравнение и находим все его действительные корни. Числаявляются собственными значениями линейного оператораА.

Для каждого собственного значения записываем однородную систему уравненийи находим ее фундаментальную систему решений. Решения фундаментальной системы являются собственными векторами линейного оператораА.

Условие задачи

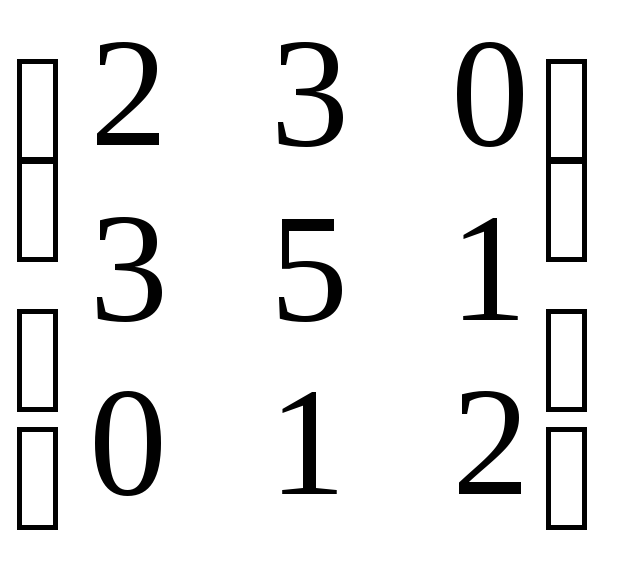
Найти собственные значения и собственные векторы линейного оператора Α, заданного в некотором базисе матрицей А (табл. 6).

Таблица 6

№	Матрица А	№	Матрица А	№	Матрица А
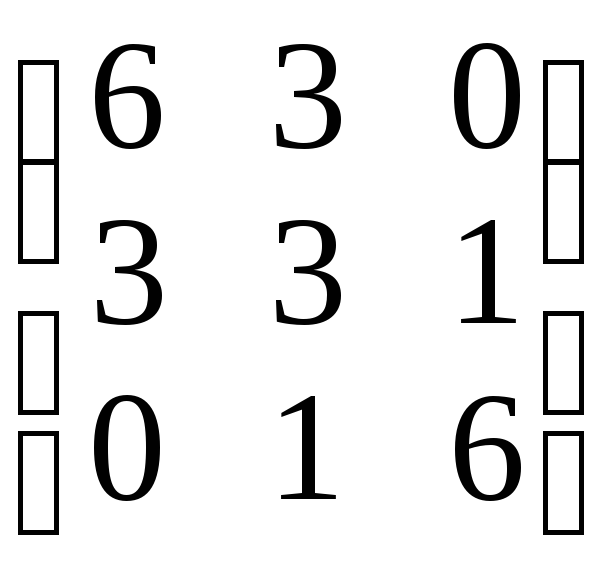
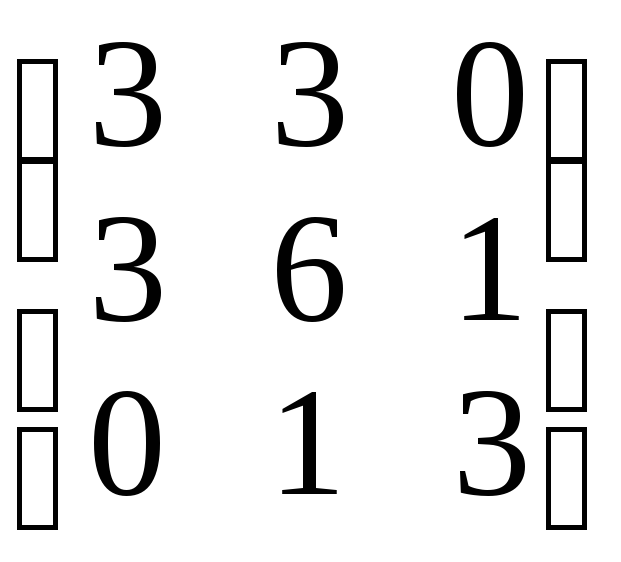
1		2		3

Окончание табл. 6

№	Матрица А	№	Матрица А	№	Матрица А
4		5		6
7		8		9
10		11		12
13		14		15
16		17		18
19		20		21
22		23		24
25		26		27
28		29		30

7. Прямая линия на плоскости

Постановка задачи

Заданы координаты точек A, B, C. Написать каноническое и общее уравнения прямой AB, найти её угловой коэффициент. Написать каноническое и общее уравнения прямой AС, найти её угловой коэффициент. Вычислить угол между прямыми AB и AС (в градусах). Написать общее уравнение высоты CD и найти её длину, не используя координаты точки D. Написать общее уравнение медианы CE. Найти координаты точки пересечения высот треугольника ABC.

План решения

Каноническое уравнение прямой, проходящей через точки М₁(x₁ ; y₁), М₂(x₂ ; y₂), имеет вид . Подставляя в это равенство координаты точек A и B (A и С), получаем искомое уравнение прямой AB (прямой АС). Преобразовываем каноническое уравнение в общее уравнение и в уравнение прямой с угловым коэффициентом.

Угол между прямыми находим из равенства , гдеk₁, k₂ – угловые коэффициенты прямых AB и AС.

Для составления уравнения высоты воспользуемся формулой уравнения прямой, проходящей через точку перпендикулярно вектору. Длину высоты CD находим по формуле расстояния от точки С до прямой АВ.

Вычисляем координаты середины отрезка АВ – точки Е. Составляем каноническое уравнение прямой, проходящей через точки С и Е. Преобразовываем каноническое уравнение в общее уравнение.

Составляем уравнение высоты BF. Координаты точки пересечения высот треугольника ABC находим, решая систему двух уравнений – уравнений высот CD и BF.

Условие задачи

Даны координаты точек A, B, C (табл. 7). Написать каноническое и общее уравнения прямой AB, найти её угловой коэффициент. Написать каноническое и общее уравнения прямой AС, найти её угловой коэффициент. Вычислить угол между прямыми AB и AС (в градусах). Написать общее уравнение высоты CD и найти её длину, не используя координаты точки D. Написать общее уравнение медианы CE. Найти координаты точки пересечения высот треугольника ABC.

Таблица 7

№	A	B	C	№	A	B	C
1	(7; 4)	(1; 1)	(4; 5)	2	(–5; 4)	(1; 1)	(–2; 5)
3	(–5; –2)	(1; 1)	(–2; –3)	4	(7; –2)	(1; 1)	(4; –3)
5	(5; 4)	(–1; 1)	(2; 5)	6	(–7; 4)	(–1; 1)	(–4; 5)

Окончание табл. 7

№	A	B	C	№	A	B	C
7	(–7; –2)	(–1; 1)	(–4; –3)	8	(5; –2)	(–1; 1)	(2; –3)
9	(7; 2)	(1; –1)	(4; 3)	10	(–5; 2)	(1; –1)	(–2; 3)
11	(–5; –4)	(1; –1)	(–2; –5)	12	(7; –4)	(1; –1)	(4; –5)
13	(5; 2)	(–1; –1)	(2; 3)	14	(–7; 2)	(–1; –1)	(–4; 3)
15	(–7; –4)	(–1; –1)	(–4; –5)	16	(5; –4)	(–1; –1)	(2; –5)
17	(8; 5)	(2; 2)	(5; 6)	18	(–4; 5)	(2; 2)	(–1; 6)
19	(–4; –1)	(2; 2)	(–1; –2)	20	(8; –1)	(2; 2)	(5; –2)
21	(4; 5)	(–2; 2)	(1; 6)	22	(–8; 5)	(–2; 2)	(–5; 6)
23	(–8; –1)	(–2; 2)	(–5; –2)	24	(4; –1)	(–2; 2)	(1; –2)
25	(8; 1)	(2; –2)	(5; 2)	26	(–4; 1)	(2; –2)	(–1; 2)
27	(–4; –5)	(2; –2)	(–1; –6)	28	(8; –5)	(2; –2)	(5; –6)
29	(4; 1)	(–2; –2)	(1; 2)	30	(–8; 1)	(–2; –2)	(–5; 2)