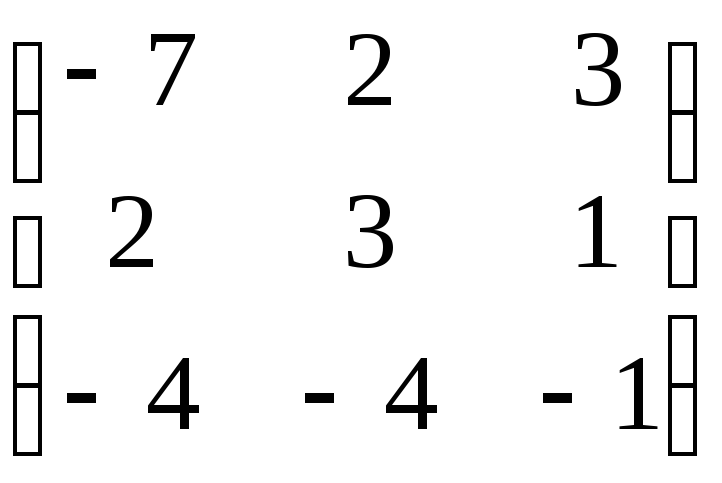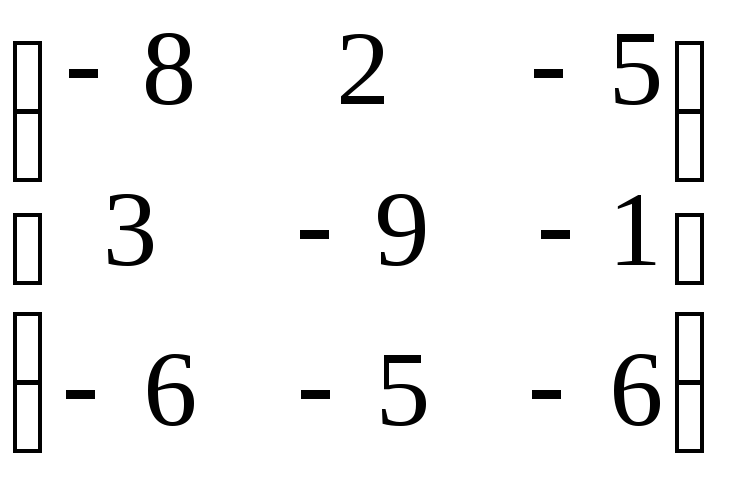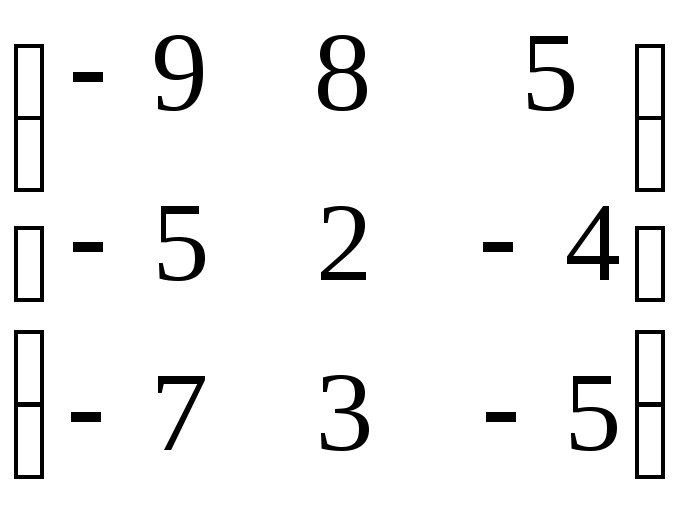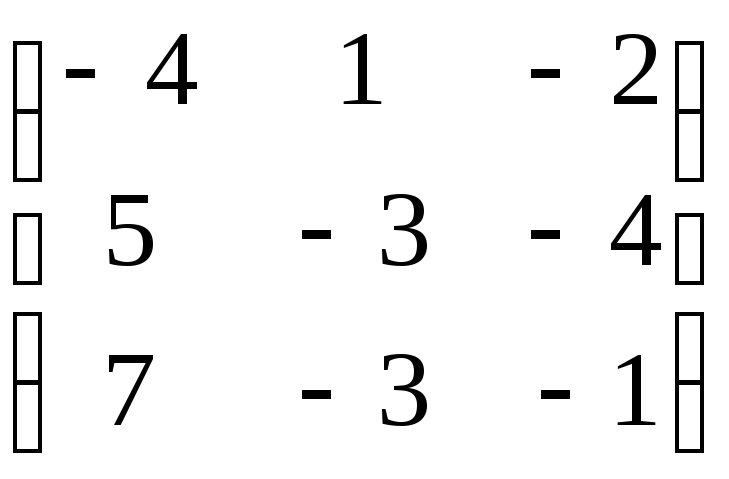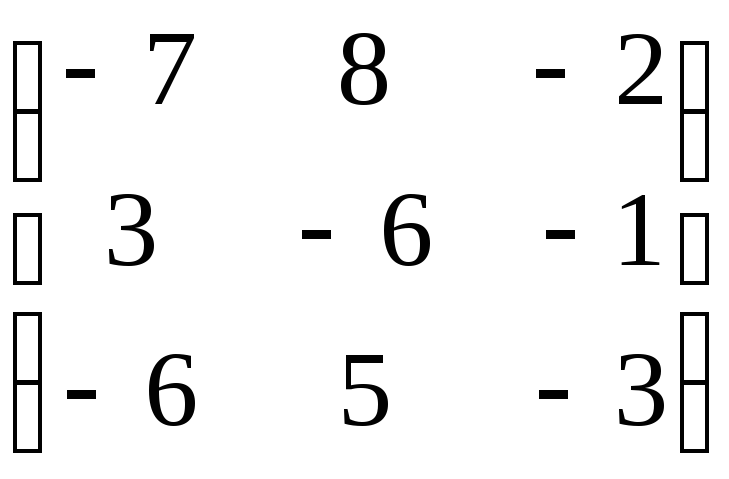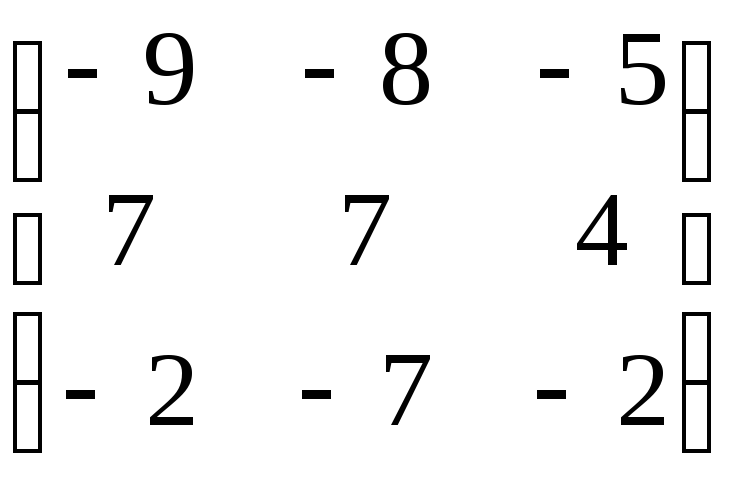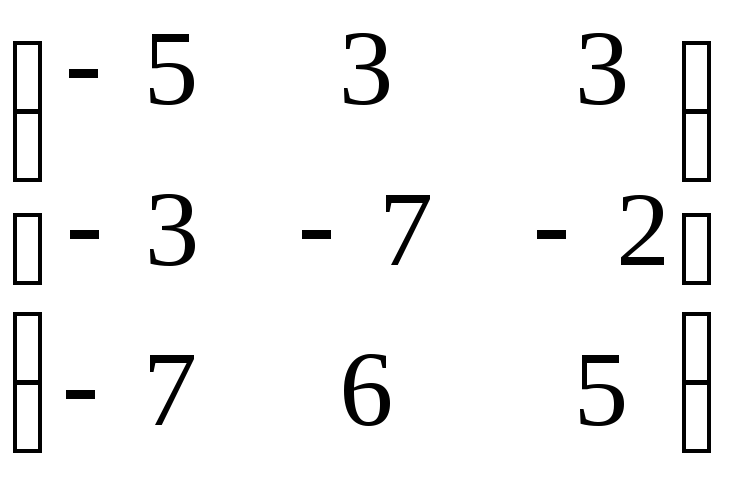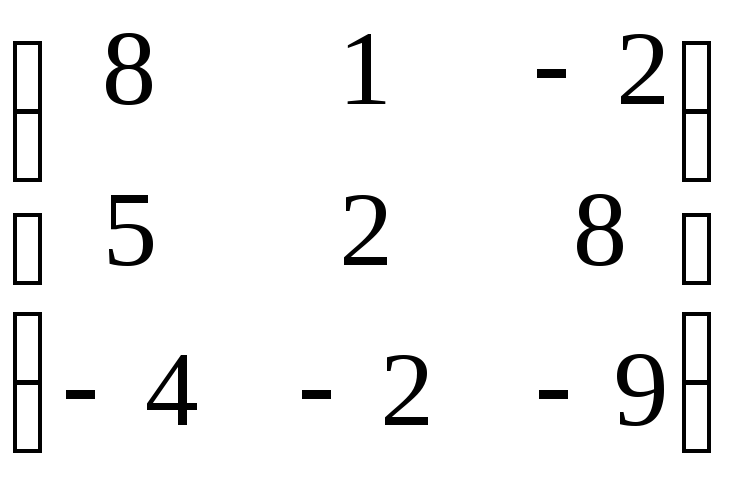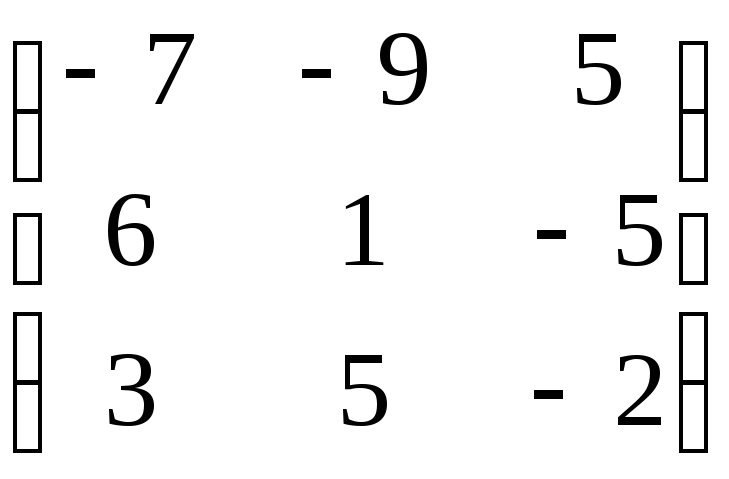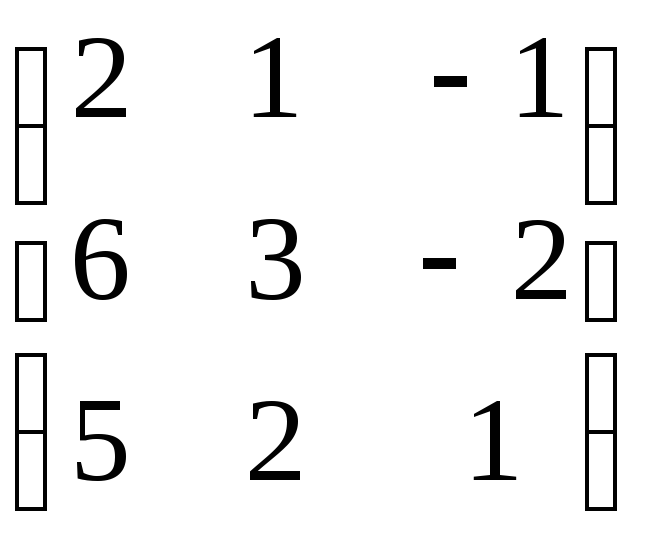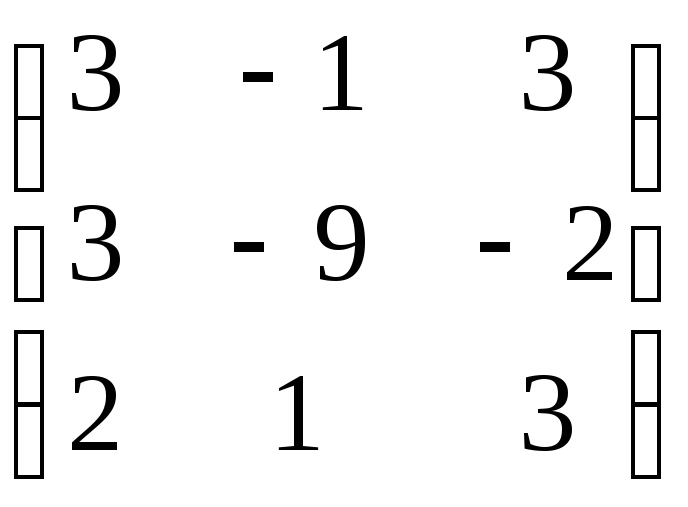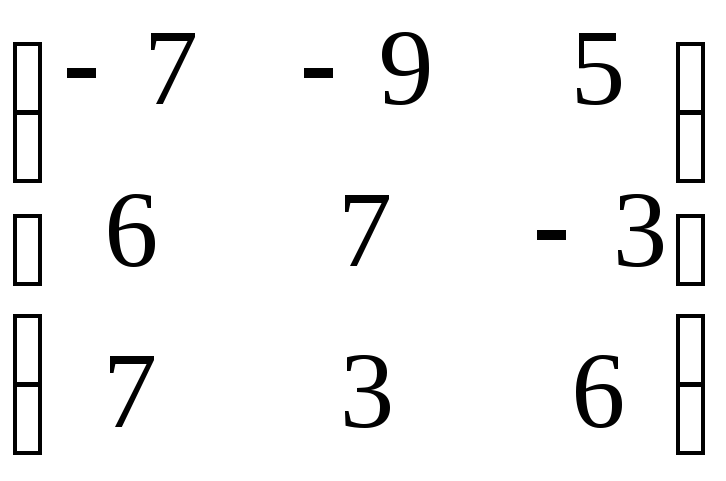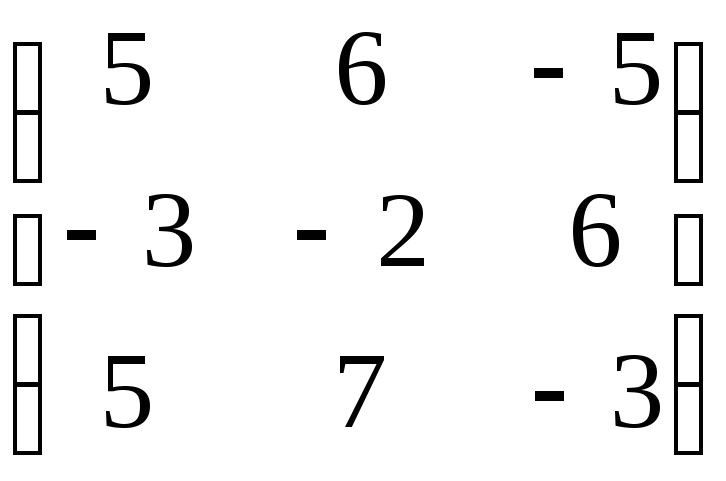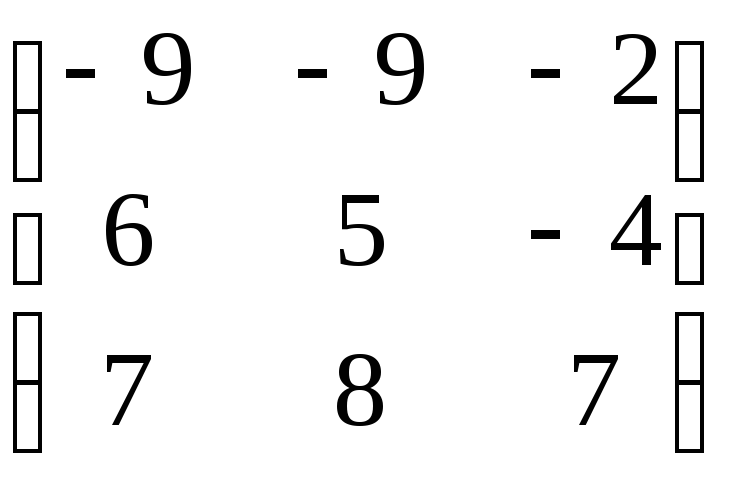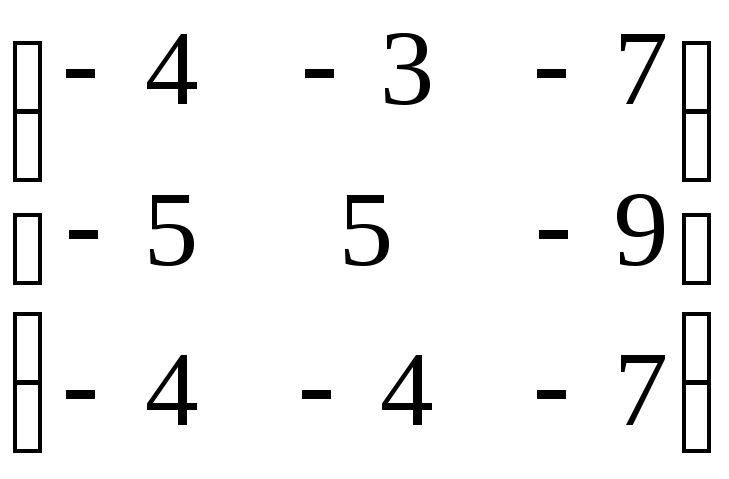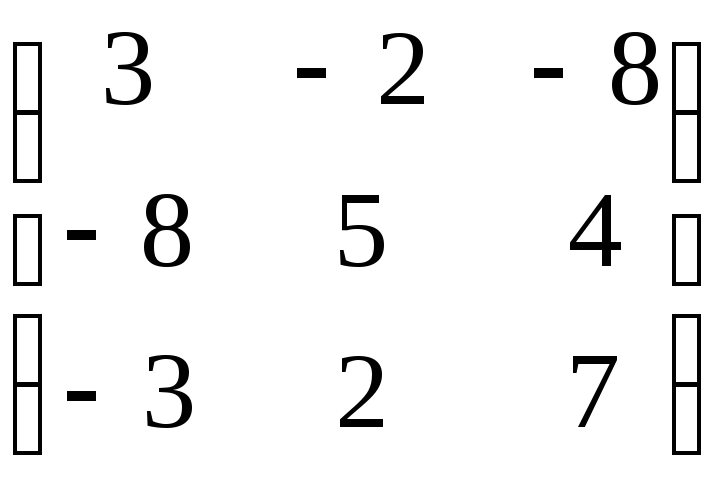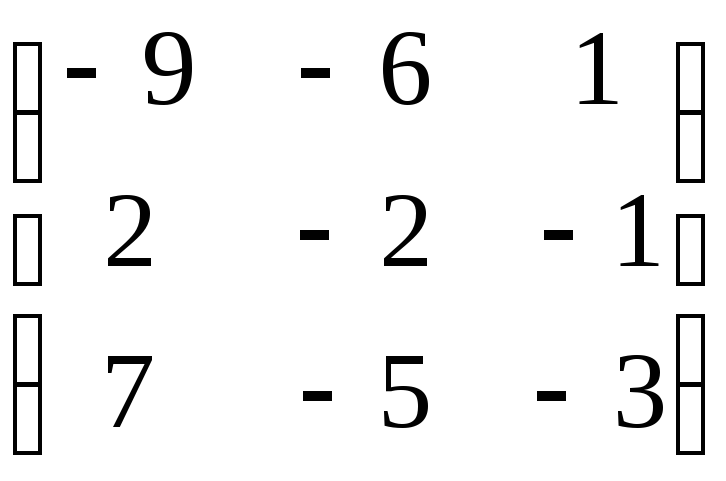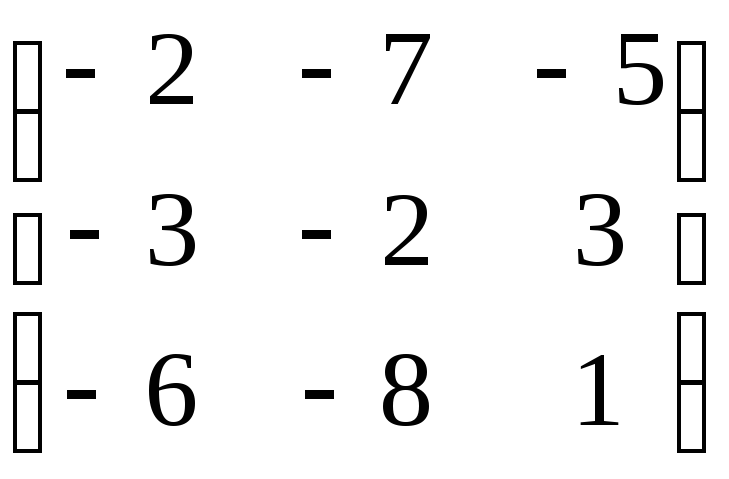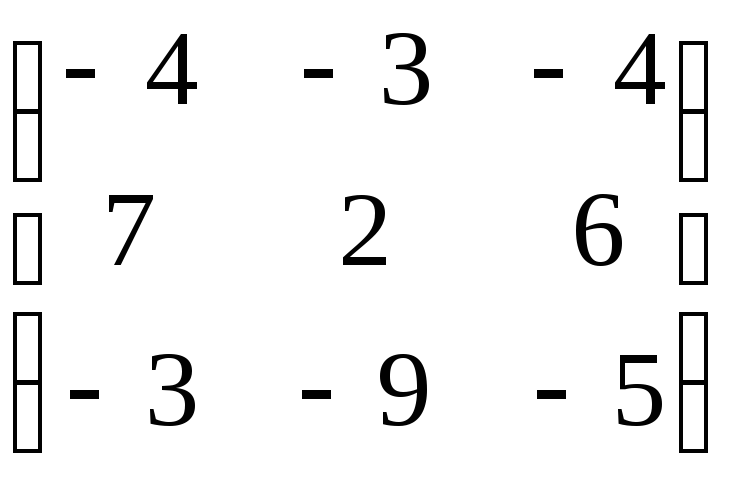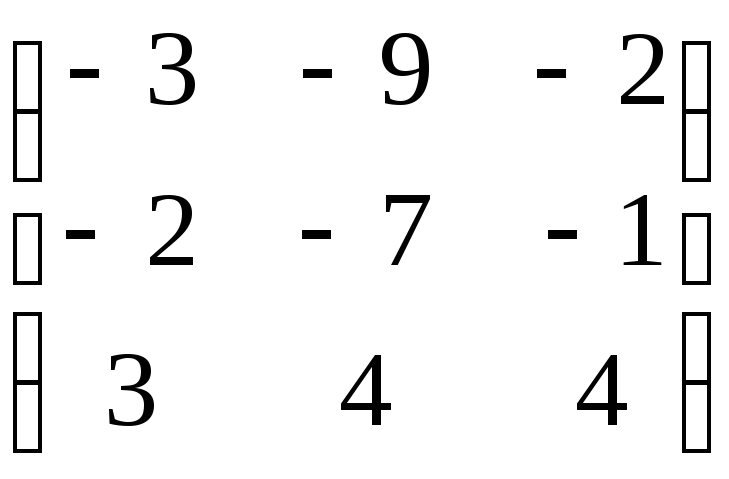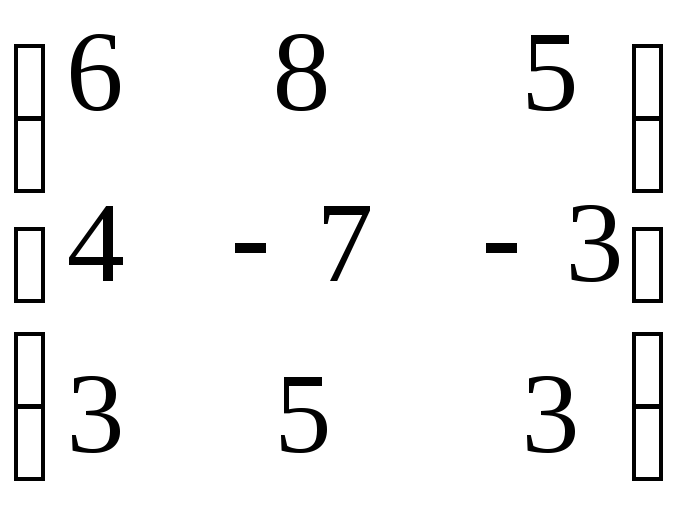Министерство образования и науки Российской Федерации

ФГБОУ ВПО «Брянский государственный технический университет»

УТВЕРЖДАЮ

Ректор университета

__________ О.Н. Федонин

«___»____________ 2013 г.

Алгебра и геометрия

Методические указания к расчетно-графической работе

для студентов очной формы обучения направлений подготовки

090900 – «Информационная безопасность» и 090303 – «Информационная безопасность автоматизированных систем»

Брянск 2013

УДК 511

Алгебра и геометрия [Текст]+[Электронный ресурс]: методические указания к расчетно-графической работе для студентов очной формы обучения направлений подготовки 090900 – «Информационная безопасность» и 090303 – «Информационная безопасность автоматизированных систем». – Брянск: БГТУ, 2013. – 19 с.

Разработал: А.И. Горелёнков, канд. техн. наук, доц.

Рекомендовано кафедрой «Высшая математика» БГТУ

(протокол №10 от 11.06.13)

ПРЕДИСЛОВИЕ

Данные методические указания предназначены для оказания помощи студентам при выполнении расчетно-графической работы (РГР).

Каждой задаче РГР отведен отдельный параграф. Он начинается с общей постановки задачи. Затем следует план решения. Параграф завершают задачи, предназначенные для самостоятельного решения.

Номер варианта соответствует порядковому номеру студента в журнале группы. Решение задач должно быть представлено к определенному сроку.

1. Матрицы и определители

Постановка задачи

Заданы квадратная матрица А и матрица-строка В. Найти матрицу С = ВАВ^т, алгебраические дополнения элементов матрицы А, обратную матрицy А^–1 элементарными преобразованиями. Решить матричные уравнения AX = В^т, YA = В и найти ранг матриц XY и YX.

План решения

Используя операцию умножения матриц, вычисляем матрицу С = ВАВ^т.

Находим алгебраические дополнения элементов матрицы А.

Вычисляем определитель матрицы А. Убеждаемся, что он не равен нулю. Следовательно, матрица А имеет обратную матрицу. К матрице А приписываем справа единичную матрицу Е. Элементарными преобразованиями над строками расширенной матрицы (A ¦ E) матрицу А приводим к виду единичной матрицы Е. После преобразований на месте приписанной справа единичной матрицы Е находится обратная матрица А^–1. Выписываем ее.

Умножая слева обе части матричного равенства АХ = В^т на А^–1, получаем решение уравнения – матрицу Х = А^–1В^т. Умножая справа обе части матричного равенства YA = В на А^–1, получаем решение уравнения – матрицу Y = BА^–1.

Вычисляем матрицы XY и YX и находим их ранг.

Условие задачи

Даны квадратная матрица А (табл. 1) и матрица-строка . Найти матрицуС = ВАВ^т, алгебраические дополнения элементов матрицы А, обратную матрицy А^–1 элементарными преобразованиями. Решить матричные уравнения AX = В^т, YA = В и найти ранг матриц XY и YX.