
Лекция 8
.docПример построения регрессионной модели
Однофакторная
линейная модель имеет вид:
![]() .
.
1). Для нахождения
коэффициентов
![]() и
и
![]() применим метод наименьших квадратов:
применим метод наименьших квадратов:
 (1)
(1)
где n – число опытов;
![]() - факторный признак;
- факторный признак;
![]() - результативный
признак.
- результативный
признак.
Если после решения
системы (1), коэффициент
![]() ,
то связь между х
и у является
прямой.
,
то связь между х
и у является
прямой.
2). Теснота этой связи определяется коэффициентов корреляции:
 .
(2)
.
(2)
Коэффициент корреляции находится в интервале от 0 до 1. Чем ближе коэффициент корреляции к единице, тем теснее связь между результативным и факторным признаками.
Средняя квадратическая ошибка выборки:
 ,
(3)
,
(3)
где
![]() -
среднее арифметическое значение.
Рассчитывается по формуле:
-
среднее арифметическое значение.
Рассчитывается по формуле:
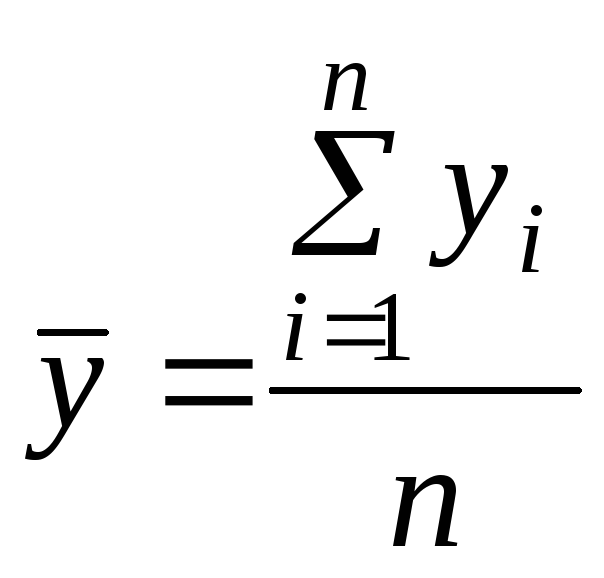 .
(4)
.
(4)
Средняя квадратическая ошибка уравнения регрессии:
 .
(5)
.
(5)
3). Коэффициент
детерминации показывает долю изменения
результативного признака под воздействием
факторного признака:
![]() .
.
4). Коэффициент эластичности показывает, на сколько процентов изменятся результативный признак при изменении факторного признака на 1%. Коэффициент эластичности рассчитывается по формуле:
![]() ,
(6)
,
(6)
где
![]() - среднее арифметическое значение
факторного признака,
- среднее арифметическое значение
факторного признака,
![]() -
среднее арифметическое значение
результативного признака.
-
среднее арифметическое значение
результативного признака.
5). Бетта - коэффициент показывает, на сколько изменится результативный признак, если изменится факторный:
![]() ,
(7)
,
(7)
где
![]() ,
,
![]() - средние квадратические ошибки выборки.
- средние квадратические ошибки выборки.
6). Средняя по модулю относительная ошибка аппроксимации:
![]() .
(8)
.
(8)
7). Среднее квадратическое отклонение:
![]() ,
где к
– количество признаков.
(9)
,
где к
– количество признаков.
(9)
