Chapter 5. Plate and Shell Elements

Chapter 5. Plate and Shell Elements

I.Plate Theory

•Flat plate

•Lateral loading

•Bending behavior dominates

Note the following similarity:

1-D straight beam model Ù 2-D flat plate model

Applications:

•Shear walls

•Floor panels

•Shelves

•…

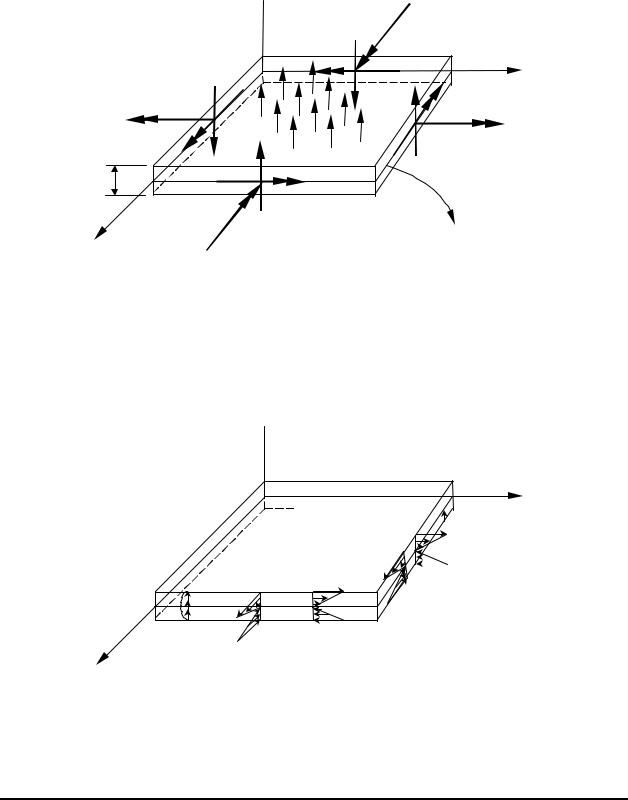
Forces and Moments Acting on the Plate:

z

∆y

Mxy

Stresses:

z

τyz y

σy

τxy

x

Relations Between Forces and Stresses

Bending moments (per unit length):

•Maximum stress is always at z = ±t / 2

•No bending stresses at midsurface (similar to the beam model)

Thin Plate Theory ( Kirchhoff Plate Theory)

Assumptions (similar to those in the beam theory):

A straight line along the normal to the mid surface remains straight and normal to the deflected mid surface after loading, that is, these is no transverse shear deformation:

γ xz =γ yz = 0.

Displacement:

w

x

Strains:

εx = −z ∂∂2 w ,

x2

Note that there is no stretch of the mid surface due to the deflection (bending) of the plate.

Stresses (plane stress state):

Main variable: deflection w = w(x, y) .

q = lateral distributed load (force/area).

Compare the 1-D equation for straight beam:

EI d 4 w = q(x). dx 4

Note: Equation (10) represents the equilibrium condition in the z-direction. To see this, refer to the previous figure showing all the forces on a plate element. Summing the forces in the z- direction, we have,

Qx ∆y +Qy ∆x + q∆x∆y = 0,

which yields,

∂∂Qxx + ∂∂Qyy + q(x, y) = 0.

Substituting the following relations into the above equation, we obtain Eq. (10).

Shear forces and bending moments:

The fourth-order partial differential equation, given in (10) and in terms of the deflection w(x,y), needs to be solved under certain given boundary conditions.

where n is the normal direction of the boundary. Note that the given values in the boundary conditions shown above can be non-zero values as well.

sn

boundary