36. Предел функции в точке. Односторонние пределы.

Число А называется пределом функции f (х), если для любого как угодно малого положительного числа ε > 0 существует зависящее от ε число δ >0, такое, что для всех х, удовлетворяющих неравенству 0 < | х - х0| < δ выполняется неравенство | f (х) – А | < ε.

Левый и правый пределы функции в данной точке условно записывают как

37. Предел функции в бесконечности. Бесконечно большие функции. Бесконечно малые фнкции и их свойства.

1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

38. Основные свойства пределов.

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

Предел разности равен разности пределов, если каждый из них существует, т.е.

Предел постоянной величины равен самой постоянной величине:

Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

Предел произведения равен произведению пределов, если каждый из них существует, т.е.

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

Предел степенной функции

где степень p - действительное число.

Предел показательной функции

где основание b > 0.

Предел логарифмической функции

где основание b > 0.

Теорема "о двух милиционерах"

Предположим, что для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если

то

То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.

39. Первый замечательный предел

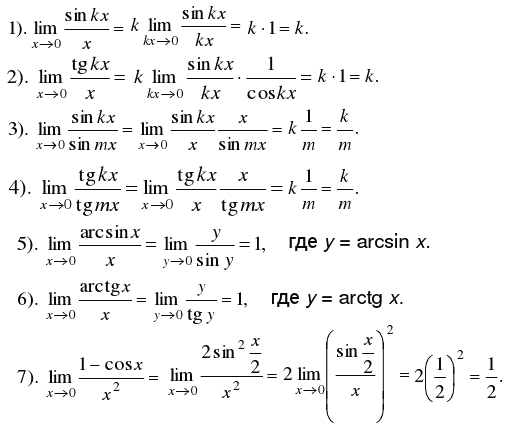
40. Второй замечательный предел.

41. Сравнение бесконечно малых.

42. Определение непрерывности в точке функции. Точка разрыва функции и их классификация.

43.Производная функции в точке.Уравнения касательной и нормали к графику функции. Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

44. Основные правила дифференцирования функций. Производная сложных функций.

Производная сложной функции ищется по следующему правилу:

(f(x(g(h)))`=f`(x)*x`(g)*g`(h)

45. Таблица производных элементарных функций.

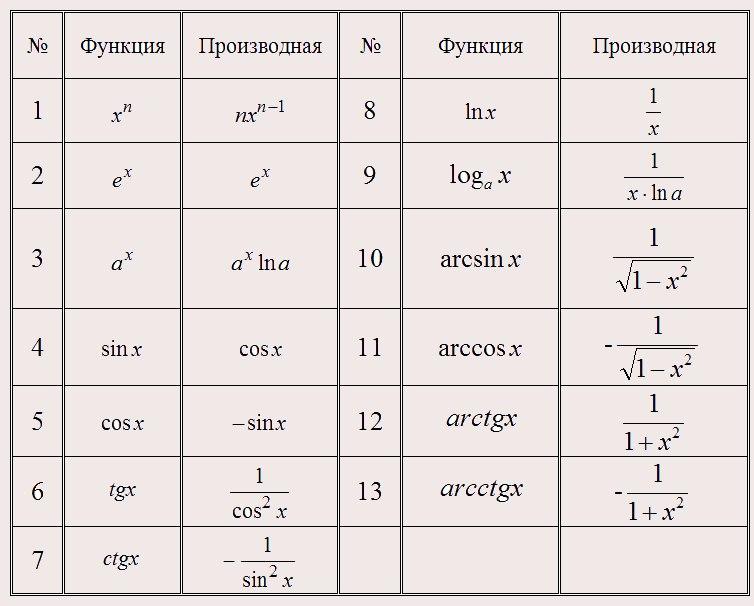
46. Дифференциал функции. Производные и дифференциалы высших порядков.

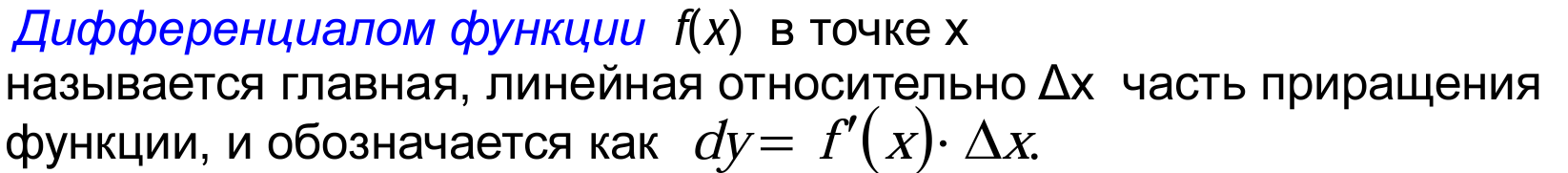
47. Дифференцирование папраметрически заданных функций. Логарифмическое дифференцирование

параметрически заданные функции дифференцируются абсолютно также, как и обычные функции, такие как, например, у=х или у=sinx

ДЛЯ. ПРОВЕДЕНИЯ ЛОГАРИФМИЧЕСКОГО ДИФФЕРЕНЦИРОВАНИЯ НУЖНО ПРОЛОГАРИФМИРОВАТЬ ОБЕ ЧАСТИ УРАВНЕНИЯ У=F(X) В. ИТОГЕ ПРИДЕМ ВОТ В ТАКОМУ ДРУГУ- У'=У*LN F(X) ТУТ НАТУРАЛЬНЫЙ ЛОГАРИФМ

48. Основные теоремы о дифференцируемых функциях (теоремы Ролля, Лагранжа и Коши).

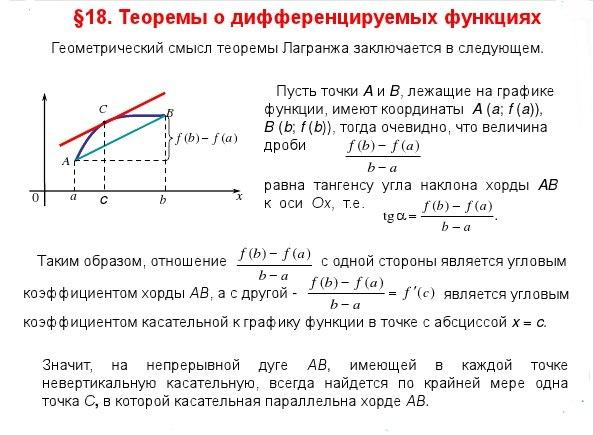
1.Теорема Ролля: фор-ка: Если функция f(x): 1) непрерывна на замкнутом промежутке [a,b]; 2) дифференцируема в каждой точке интервала (a,b); 3) на концах отрезка принимает равные значения (f(a)=f(b)), то тогда между точками a и b найдется хотя бы одна точка c (a<c<b) такая что f'(c)=0. Геометрический смысл теоремы Ролля состоит в следующем: Если выполнены условия теоремы Ролля, то в некоторой точке x = c f '(c) = 0, а это означает, что внутри интервала всегда найдется точка x = c, касательная к графику функции y = f (x) в которой параллельна оси Ох. 2.Теорема Лагранжа.  Пусть функция y = f (x): 1) непрерывна на замкнутом промежутке [a, b], 2) дифференцируема на интервале (a, b) . Тогда внутри промежутка [a, b] найдется хотя бы одна точка c (a < c < b) такая, что будет иметь место равенство f (b) - f (a) = f'(c)(b - a)– формула Лагранжа. Геометрический смысл теоремы Лагранжа (см. рис1.) 3.Теорема Коши. Пусть функции f(x) и g(x) 1) непрерывны на отрезке [a, b], 2) дифференцируемы в каждой точке интервала (a, b) , 3) производная g'(x) не равна 0 ни в одной точке этого интервала. Тогда между точками a и b существует такая точка c (a < c < b), что имеет место равенство f'(c)/g'(c)=(f(b)-f(a))/(g(b)-g(a))

49. Правило Лопиталя и раскрытие с его помощью всех видов неопределенностей. Определение: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному). Правило Лопиталя. Для раскрытия неопределенностей 0/0 бесконечность/бесконечность надо заменить предел отношения двух функций пределом отношения их производных. Если окажется, что отношение производных имеет конечный предел, то к этому же пределу стремится и отношение данных функций. Если неопределенность не раскрылась после применения правила Лопиталя, это правило можно применить еще раз, но уже к отношению производных (при условии, что отношение производных f'(x)/g'(x) порождает неопределенности 0/0 беск/беск Н/п см. рис

50. Условие возрастания и убывания функций. Максимум и минимум функций. Достаточный признак существования экстремума функций.

1.Исследование функций с помощью первой производной  Признаки возрастания и убывания функции  Теорема. Пусть функция y=f(x) непрерывна на промежутке [a,b] и дифференцируема в каждой точке интервала (a, b). F(x) –монотонно возрастает при f’(x)>0 F(x) – монотонно убывает при f’(x)<0 2.Экстремумы функции  Определение. Значение функции в точке x0 называется максимумом (минимумом) f(x), если существует такая окрестность точки x0, во всех точках которой выполняется условие f(x0)>f(x). (f(x0)<f(x)). Точка x0 при этом называется точкой локального максимума (минимума).  Максимум или минимум функции обозначаются одним словом: экстремум. Теорема (необходимое условие существование экстремума функции). Если функция f(x) дифференцируема в некоторой точке x0, принадлежащей интервалу (x0-(сигма); x0+(сигма)) и имеет в этой точке экстремум, то f’(x0)=0. Замечание 1. Условие теоремы не является достаточным.  Замечание 2. Касательная к графику дифференцируемой функции в точке экстремума параллельна оси Ox .  Замечание 3. Экстремум может также существовать в точке, в которой производная не существует.  Определение. Точка x0 называется критической точкой первого рода функции y=f(x), если в этой точке производная функции равна нулю или не существует.  Определение. Критическая точка первого рода функции y=f(x), в которой производная равна нулю, называется стационарной точкой этой функции.  У функции может быть экстремум только в критических точках первого рода, поэтому иначе они называются точками, подозрительными на экстремум Первый достаточный признак экстремума  Теорема. Если функция f (x) дифференцируема в некоторой окрестности точки x0 и производная f ‘(x) обращается в нуль в точке x0, то:  если при прохождении через точку x0 производная меняет знак “плюс” на “минус”, то в точке x0 функция имеет максимум;  если при прохождении через точку x0 производная меняет знак “минус” на “плюс”, то в точке x0 функция имеет минимум.

51.порядок нахождения наибольшего и наименьшего значений функции на отрезке Пусть функция f (x) непрерывна на промежутке [a, b]. Тогда на этом промежутке она имеет наибольшее и наименьшее значения. Для нахождения наибольшего и наименьшего значений непрерывной на промежутке [a, b] функции f(x) необходимо:  1) найти все критические точки функции на интервале (a, b), 2) вычислить её значения в этих точках, 3) найти значения функции на концах интервала, 4) из полученных значений выбрать наибольшее и наименьшее

52. Выпуклость и вогнутость графика функции. Точки перегиба графика. Достаточный признак существования перегиба.

Вторая производная. Если производная  f ' ( x ) функции  f ( x )дифференцируема в точке ( x₀ ), то её производная называетсявторой производной функции  f ( x )  в точке ( x₀ ), и обозначается  f '' ( x₀ ).  

 

Функция  f ( x ) называется  выпуклой  на интервале ( a, b ), если её график на этом интервале лежит  ниже  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀ (a, b ).

Функция  f ( x ) называется  вогнутой на интервале ( a, b ), если её график на этом интервале лежит  выше  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀ (a, b ).

 

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторуюпроизводную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x (a, b ), то функция  f ( x ) являетсявогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x (a, b ), то функция  f ( x ) являетсявыпуклой на интервале ( a, b ) .

 

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.Отсюда следует, что если в точке перегиба  x₀  существует вторая производная  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

53. Асимптоты графика функции. Прямая линия называется асимптотой, если расстояние между текущей точкой графика и этой прямой стремится к нулю по мере удаления точки от начала координат.  Бывают вертикальными и наклонными. Вертикальные: если функция имеет точку разрыва, в которой хотя бы один предел бесконечен, то вертикальная прямая (параллельная оси ординат), проходящая через эту точку, называется вертикальной асимптотой. Функция может иметь бесконечно много вертикальных асимптот. Наклонные: если следующие пределы существуют и конечны, то прямая y=kx+b является наклонной асимптотой. Если k и b равны нулю, то получаем частный случай наклонной асимптоты y=0 (горизонтальная асимптота)

54. Общая схема исследования графика функции. 1) Область определения 2) Чётн, нечётн, периодичность 3) Точки разрыва 4) Асимптоты 5) Точки пересечения с осями 6) Монотонность и экстремумы 7) Выпуклость, вогнутость, перегибы 8) Построение графика