
- •«Изучение собственных колебаний в электромагнитном контуре»
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •4. Техника безопасности
- •5. Порядок выполнения работы
- •6. Обработка результатов измерений
- •«Изучение собственных колебаний в электромагнитном контуре»
- •1. Введение
- •2. Основные понятия
- •3. Описание лабораторной установки
- •4. Техника безопасности
- •5. Порядок выполнения работы
- •6. Обработка результатов измерений
Лабораторная работа № 3-КМ
«Изучение собственных колебаний в электромагнитном контуре»
1. Введение
1.1. Собственные колебания в изолированной системе происходят после окончания внешнего воздействия, которое вывело её из положения равновесия. Частота колебаний в этом случае определяется только свойствами самой системы.
1.2. В реальных колебательных системах, будь то механические или электромагнитные, процесс колебаний всегда сопровождается диссипацией (рассеянием энергии), в силу чего колебания будут затухать. В одних случаях затухание в системе стремятся сделать как можно меньше, в других - искусственно увеличивают (вводят демпфирование).
1.3. Пользуясь универсальностью законов колебаний, можно изучать поведение механической системы на аналогичной ей электромагнитной. В этом случае изменять затухание в системе очень просто – изменяя величину активного сопротивления.
1.4. Целью настоящей лабораторной работы является экспериментальное ознакомление с собственными колебаниями в электромагнитном контуре и влиянием некоторых его параметров на этот процесс.
2. Основные понятия
2.1. Исходя из второго закона Кирхгофа, можно записать следующее уравнение для падений напряжения в замкнутом контуре, состоящем из индуктивности L, ёмкости С и активного сопротивления R (рис. 1):

Рис. 1

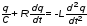 ,
(1)
,
(1)
где
q
- величина заряда на емкости; dq/dt
= i
- сила тока;
-Ldi/dt
- ЭДС самоиндукции. Введя, как обычно:
β
= R/2L
- коэффициент затухания; ω0
= - круговую частоту собственных незатухающих
колебаний , получим из (1) дифференциальное
уравнение в виде
- круговую частоту собственных незатухающих
колебаний , получим из (1) дифференциальное
уравнение в виде
 .
(2)
.
(2)
Решения этого уравнения опишут возможные процессы, происходящие в контуре при различных условиях.
При малом затухании (β < ω0) получаем решение в виде затухающих колебаний
 .
(3)
.
(3)
При критическом затухании (ω0 = β) решение имеет вид
 .
(4)
.
(4)
При затухании больше критического (β > ω0) зависимость апериодическая
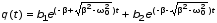 .
(5)
.
(5)
В формулах (3),(4),(5) A0, φ, a1, a2, b1, b2 - константы, зависящие от начальных условий q(0) и i(0).
Хотя функции, описывающие q(t), различны, их графики непрерывно переходят один в другой при плавном изменении коэффициента затухания.
2.2. Для характеристики степени затухания в контуре, кроме величины β, используют логарифмический декремент затухания λ - он равен натуральному логарифму отношения двух последующих амплитуд (отличающихся по времени на период T) (рис. 2):
 .
(6)
.
(6)
Из формул (3) и (6) следует:
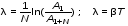 .
(7)
.
(7)

Рис. 2
2.3. В процессе колебаний энергия электрического поля конденсатора переходит в энергию магнитного поля катушки индуктивности и наоборот. Эти переходы сопровождаются потерями - выделяется тепло.
Удобно пользоваться понятием добротности контура Q, которая в радиотехнике вводится, как
 .
(8)
.
(8)
Можно показать, что при достаточно малом затухании (β <<ω0)
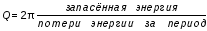 .
(9)
.
(9)
2.4. В данной лабораторной работе нужно определить период затухающих колебаний, логарифмический декремент затухания, рассчитать добротность, индуктивность и активное сопротивление контура.
2.5. Зарисовать осциллограммы колебаний.
