1)Обратная матрица

Матрица A ^{− 1} называется обратной к квадратной матрице A n –го порядка, если

A · A − 1 = A − 1 · A = E ,

Условие существования обратной матрицы. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. detA ≠ 0 .

2)Теорема об определителе произведения матриц

Пусть и— матрицы одного и того же порядка. Тогда

т.е. определитель произведения матриц равен произведению их определителей.

9. Методы обращения матрицы.

Обращение матрицы - алгоритм, применяемый при численном нахождении обратной матрицы. Как и в задаче решения линейных систем, методы численного обращения подразделяются на прямые и итерационные; однако итерационные методы вследствие их трудоемкости играют здесь существенно меньшую роль.

Большинство прямых методов О. м. основано на идее разложения заданной матрицы в произведение легко обращаемых сомножителей. Если

- такое разложение, то

Типичным (и одним из наиболее употребительных) прямых методов О. м. является метод Жордана (см. [1]).

Пусть А- невырожденная матрица порядка п. Построение обратной матрицы А ^-1 происходит в пшагов; результатом k-го шага будет матрица , первые кстолбцов к-рой совпадают с одноименными столбцами единичной матрицы. Переход от(пустьА=А ₀ )к с матричной точки зрения эквивалентен умножению .слева на матрицу, к-рая отличается от единичной лишь (k+1)-м столбцом. Элементы этого столбца выбираются так, чтобы привести (k+1)-й столбецк единичному, и имеют вид

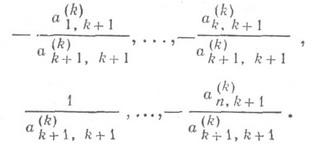
Из соотношений

вытекает

и

Получение факторизованного представления (1) для обратной матрицы требует примерноопераций умножения и примерноопераций сложения. Приблизительно такое же число дополнительных операций необходимо для того, чтобы перемножить матрицы в (1) и получить явный вид. Во многих приложениях операции О. м. использование факторизованной формы (1) столь же удовлетворительно, что и явного вида. Напр., вычисление произведения, где b- вектор-столбец, требует одинаковой арифметич. работы в обоих случаях. Одинаковы и требования к памяти при реализации на ЭВМ.

В приведенном описании метода Жордана предполагалось для простоты, что все элементы (называемые ведущими элементами) отличны от нуля. В действительности метод Жордана, как и методы типа Гаусса для решения линейных систем, как правило, применяется с той или иной схемой выбора ведущих элементов. Использование такой схемы равносильно введению в (1) дополнительных множителей, учитывающих перестановки строк и столбцов обратной матрицы. Точность вычисленного решения, как и в случае линейных систем, зависит от степени роста матричных элементов на промежуточных шагах метода. Такой рост и, следовательно, ухудшение точности вычисляемого решения в методе Жордана, даже при выборе ведущего элемента, более вероятны, чем в методах типа Гаусса.

Невязкой, соответствующей приближенной обратной матрице Xдля А, наз. матрица . Имеет место оценка

Таким образом, норма невязки является оценкой относительной точности приближенной обратной матрицы X. В этом состоит важное отличие задачи численного О. м. от задачи решения линейных систем, где (напр., в ортогональных методах или методах типа Гаусса) невязка обычно мала, а качество полученного решения зависит от обусловленности системы.

Обращение ряда важных классов матриц может быть достигнуто значительно более экономичными, чем в общем случае, методами. Таковы теплицевы, ганкелевы, ленточные (и, в частности, трехдиагональные) матрицы, блочные матрицы, имеющие теплицеву структуру или структуру кронекерова произведения, и т. д. Напр., пусть Т- теплицева матрица порядка n+1 с элементами из Rили С:

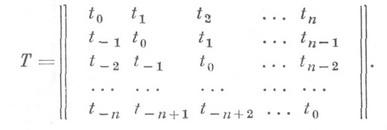
Предполагается, что не только Т, но и ее главная подматрица порядка пневырождены. Тогда для матрицы уже, вообще говоря, не являющейся теплицевой, справедливо представление (см. [2]):

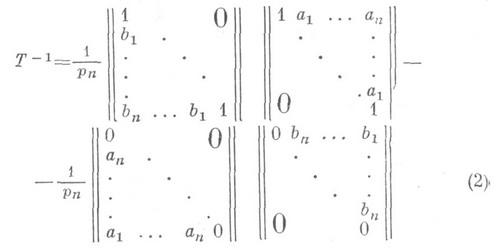
При этом векторы

суть соответственно первый и последний столбцы Таким образом, Тполностью определяется заданием первого и последнего столбцов. При необходимости из (2)могут быть последовательно вычислены все элементы

Это вычисление требует арифметич. операций.

В экономичных алгоритмах обращения теплицевых. матриц (см., напр., [3]) вычисление проводится по рекуррентным формулам и также требуетопераций. Условие невырожденности главных подматриц может быть ослаблено с сохранением порядка О( п ² )необходимой арифметич. работы.