30. Достаточные условия экстремума.

 Теорема. Пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х₁, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х₁. Если при переходе слева направо через эту точку х₁ производная меняет знак с плюса на минус, то при х = х₁ функция имеет локальный максимум. Если же при переходе слева направо через эту точку х₁ производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум.    Комментарий. Если в достаточно малой окрестности точки х₁ справедливо f ' (x) > 0 при х < x₁, f ' (x) < 0 при х > x₁, то в точке х₁ функция имеет максимум; если f ' (x) < 0 при х < x₁, f ' (x) > 0 при х > x₁, то в точке х₁ функция имеет минимум.    Доказательство. Пусть при переходе слева направо через эту точку х₁ производная меняет знак с плюса на минус, то есть для всех х, достаточно близких к х₁, имеем f ' (x) > 0 при х < x₁, f ' (x) < 0 при х > x₁. Применяя теорему Лагранжа к разности f (x) − f ( x₁), получим

f ( x ) − f ( x₁ ) = f ' ( c )·( x − x₁ ).

где с лежит между точками х и х₁. По условию теоремы

sign f ' ( c ) = − sign ( x − x₁ ),

поэтому в произвольно малой окрестности точки х₁ имеем

f ( x ) < f ( x₁ ).

В этом случае точка х₁ есть точка локального максимума, что и требовалось доказать.

31. Асимптоты вертикальные и наклонные

• Аси́мпто́та^[1] (от греч.ασϋμπτωτος — несовпадающий, не касающийся) кривойсбесконечнойветвью —прямая, обладающая тем свойством, что расстояние от точки кривой до этойпрямойстремится к нулю при удалении точки вдоль ветви вбесконечность^[2]. Термин впервые появился у Аполлония Пергского, хотя асимптотыгиперболыисследовал ещёАрхимед^[3].

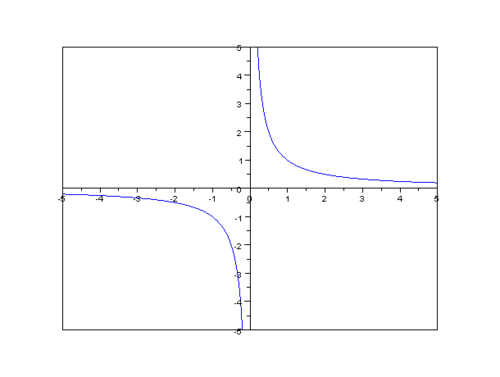
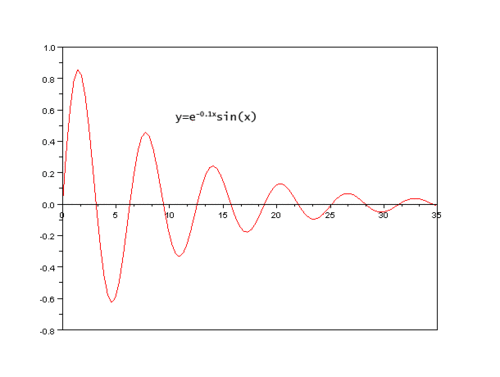
Для гиперболы асимптотами являются оси абсцисс и ординат.Криваяможет приближаться к своей асимптоте, оставаясь с одной стороны от нее	Затухающие колебания. .Криваяможет бесконечное множество раз пересекать асимптоту
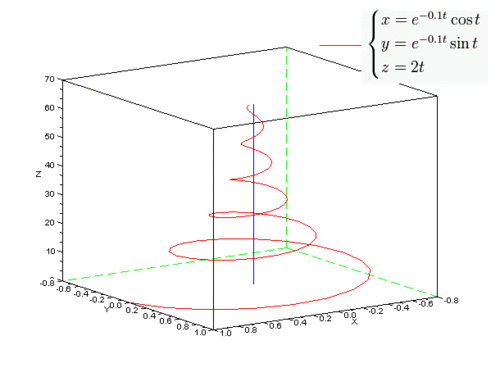
Пример асимптоты для кривой в пространстве. Спираль бесконечно приближается к прямой

   Вертикальные асимптоты

     1. Линия задана уравнением y = f(x). Если , тоx = a - вертикальная асимптота. В частности, если , тоx = a - вертикальная правосторонняя асимптота; если же , тоx = a - вертикальная левосторонняя асимптота.

     2. Линия задана уравнениями x = x(t), y = y(t). Если ,, тоx = a - вертикальная асимптота. В частности, если ,, тоx = a - вертикальная правосторонняя асимптота; если же ,, тоx = a - вертикальная левосторонняя асимптота.

     Наклонные асимптоты

     1. Линия задана уравнением y = f(x).

     Если , то прямаяy = kx + b - наклонная асимптота. При этом

     Если , то прямаяy = kx + b - наклонная асимптота вправо,

     Если , то прямаяy = kx + b - наклонная асимптота влево,

     1. Линия задана уравнениями x = x(t), y = y(t).

     Если (a - конечное число либо один из символов ) и линия обладает асимптотойy = kx + b, то

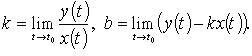
32. Выпуклость. Точки перегиба

Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 € ( a, b ).

Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 € ( a, b ).

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если f '' ( x ) > 0 для любого x € ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

если f '' ( x ) < 0 для любого x € ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0

.П р и м е р . Рассмотрим график функции y = x3 :

Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6x, но 6x > 0 при x > 0 и 6x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x3 является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x3.