2. Алгебра матриц (сложение, умножение на число, умножение матриц, линейная комбинация, транспонирование)

Сложение матриц 

     Суммой матриц иодинаковых размеров называется матрицатех же размеров, у которойОбозначение:C = А + В.

     Свойства сложения матриц: А + В = В + А, (А + В) + С = A + (B + C), А + 0 = A, А + (-A) = 0, A, B, C.

 Умножение матрицы на число 

     Произведением матрицы на числоназывается матрицатех же размеров, у которойОбозначение:

     Свойства ,и

Умножение матриц 

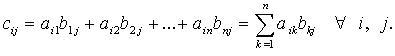    Произведением матрицы размеромна матрицуразмеромназвается матрицаразмерому которойОбозначение:C = AB.

     Свойства AE = EA = A, AO = OA = O, (AB)D = A(BD), (AB) = (A)B = A(B), (A + B)D=AD + BD, D(A + B) = DA + DB (при условии, что указанные операции имеют смысл).

     Для квадратных матриц А и B, вообще говоря,      Транспонирование матриц 

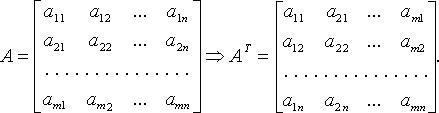
     Свойства: 

Линейной комбинацией матриц A и B называется выражение вида  , гдеи   – числовые коэффициенты.

3. Подстановки, транспозиции и их свойства.

Определение 1. Произвольное взаимно однозначное отображение множества первых натуральных чисел называетсяподстановкой1) -го порядка.

Замечание 1. Часто подстановки называют перестановками.

Обычно подстановку изображают следующим образом:, что задает образы всех элементов:,и так далее. Также используют запись.

Пример 1. Подстановку можно записать также в виде, так как в обоих случаях мы имеем отображение,,.

Определение 2. Элемент подстановкиназывается действительно перемещаемым, если.

Пример 2. В подстановке два действительно перемещаемых символа: 1 и 3.

Операция умножения на подстановках определяется как композиция отображений, причем знак композиции обычно опускают

Транспозиции и циклы

Определение 3. Циклической подстановкой2), или циклом3) называется такая подстановка , что при повторении ее достаточное число раз всякий из действительно перемещаемых ею символов может быть переведен в любой другой из этих символов. Для обозначения цикла используют запись, где— число действительно перемещаемых символов подстановки, которое называется длиной цикла4).

Пример 3. В подстановке

действительно перемещаемыми символами являются 1, 3, 4, 5, 6. Выберем любой из них, например, 3. ,. Поэтому цикл можно записать как.

Определение 4. Циклы называются независимыми5), если они не имеют общих действительно перемещаемых символов.

Предложение 1. Любая подстановка изможет быть разлжена в произведение попарно независимых циклов. Такое представление определено однозначно с точностью до порядка перемножения циклов.

Пример 4. — разложение подстановки в произведение попарно независимых циклов.

Определение 5. Цикл длины 2 называется транспозицией6).

Предложение 2. Каждая подстановка может быть представлена в виде произведения транспозиций.

Доказательство.

В отличие от представления в произведение попарно независимых циклов, представление в виде произведения транспозиций может не быть единственным.

Пример 5. Подстановка может быть разложена в произведение транспозицийили.

Четность подстановки

Определение 6. Пусть — разложение подстановкив произведение транспозиций. Тогда числоназываетсязнаком7)(четностью) подстановки . Подстановка называется четной8), если и нечетной9) в противном случае.

Предложение 3. Четность подстановки не зависит от способа разложения подстановки в произведение транспозиций.

Предложение 4. Для двух подстановок ичетность их произведения равна произведению четностей:

.

Доказательство.

Предложение 5. Пусть — цикл длины. Тогда его четность равна.

Доказательство.

Определение 7. Пусть — разложение подстановки в произведение независимых циклов длин. Числоназывается декрементом10) подстановки .

Предложение 6. Пусть — разложение подстановки в произведение независимых циклов длин. Тогда четность подстановкивычисляется по формуле

.

Доказательство.

Пример 6. Любая транспозиция — это нечетная подстановка. Подстановка из примера 4 нечетная, так как декремент — нечетное число.

Пример 7. Любая подстановка, в разложении которой на независимые циклы все циклы имеют нечетные длины , четна, так как ее декремент — это суммачетных чисел.