27. Формула Тейлора.

Тейлора формула, формула

  

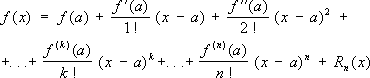
28. Применение производной для исследования монотонности функции.

Моното́нная фу́нкция — это функция, приращениекоторой не меняет знака, то есть либо всегда отрицательное, либо всегда положительное[1]. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Свойства монотонных функций

• Монотонная функция, определённая на интервале,измеримаотносительноборелевских сигма-алгебр.

• Монотонная функция, 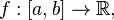определённая назамкнутоминтервале,ограничена. В частности, онаинтегрируема поЛебегу.

• Монотонная функция может иметь разрывы только первого рода. В частности,множествоточек разрыване более чем счётно.

• Монотонная функция 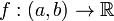дифференцируемапочти всюдуотносительномеры Лебега.

Связь характера монотонности функции и ее производной:

• если функция возрастает на промежутке и имеет на нем производную, то производная неотрицательна;

• если функция убывает на промежутке и имеет на нем производную, то производная неположительна.

При исследовании функции на монотонность берут только открытые промежутки, т.е. интервалы или открытые лучи. Дело в том, что для функции, определенной на отрезке [а, Ь], не очень корректно ставить вопрос о существовании и о значении производной в концевой точке (в точке х= а или в точке х= Ъ), поскольку в точке х = а приращение аргумента может быть только положительным, а в точке х = Ъ — только отрицательным. В определении производной такие ограничения не предусмотрены.

Теорема1. Если во всех точках открытого промежутка Х выполняется неравенство f’≥0, то функция y=f возрастает на всем промежутке Х. Теорема2. Если во всех точках открытого промежутка Х выполняется неравенство f≤0, то функция y=f убываеи на всем промежутке Х. Теорема3. Если во всех точках открытого промежутка Х выполнчяется равенство f=0, то функция y=f постоянна на промежутке Х.

29. Минимумы и максимумы функции. Необходимые условия экстремума.

Экстре́мум (лат.extremum — крайний) в математике — максимальное или минимальное значение функциина заданноммножестве. Точка, в которой достигается экстремум, называетсяточкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализевыделяют также понятиелокальный экстремум (соответственно минимум или максимум).

Определение 1. Точку х =х₀ называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х =х₀) выполняется неравенство: f(х)>f(х0).

Определение 2. Точку х = х₀ называют точкой максимума функции у=f(х), если у этой точки существует окрестность, для всех точек которой, кроме самой точки х = х₀, выполняется неравенство: f(х)<f(х₀).

Необходимое условие экстремума

         Функция z = f ( x, y) может иметь экстремум лишь в тех точках, в которых обе частные производные обращаются в ноль или перестают существовать.    Действительно, фиксируя попеременнох = х₀ или у = у₀, получим попеременно функцию одного аргумента, для которой воспользуемся необходимым условием экстремума функции одного переменного.    Эта теорема не является достаточной, но позволяет находить точки, «подозрительные на экстремум».

Теорема 4. Если функция у = f(х) имеет экстремум в точке х = х₀, то в этой точке производная функции либо равна нулю, либо не существует.